数字信号处理在wav信号分析方面的应用

黄荷洁

(陕西国际商贸学院 电子与信息工程系，陕西 西安 712000)

随着信息技术的飞速发展，数字信号处理理论和技术日益成熟，在各个领域都得到了广泛的应用。本文将通过分析计算机中的wav文件来讨论数字信号处理中的信号分析方法。

1 wav文件的一次性傅里叶变换

我们选择一个wav文件作为分析的对象，先选择一个简单的wav文件。这里选择的是每个windows系统都有的ding.wav，一个比较单纯的声音“叮……”。

1.1 声波主要频率的分析

首先执行下面的语句：

该信号的时域波形如图1所示，有size(y)语句可以得到结果为20191，即需要处理的数据量很大，所以对其进行FFT分析所需要的点数为32768。求出频谱最大值及其对应的位置为m=490.3636，k=1171。显示的频域幅值如图2所示，从图中可以看出它是以x=32768/2对称的，而且除了1171一点之外，在坐标4000～5000之间还有一个峰值。此外，由我们在“离散傅里叶变换”学习的相关知识，可以得到这两个峰值所代表的频率是，所以接着运行以下语句：

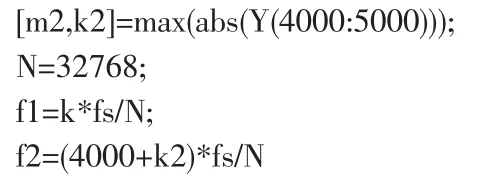
得结果m2=22.6522，k2=717。还求出第一个峰值所代表的频率为f1=787.9807，即787Hz；第二个峰值所代表的频率为f2=(4000+717)/72768*fs，即为3174Hz。这样就完成了对该声波主要频率的分析。

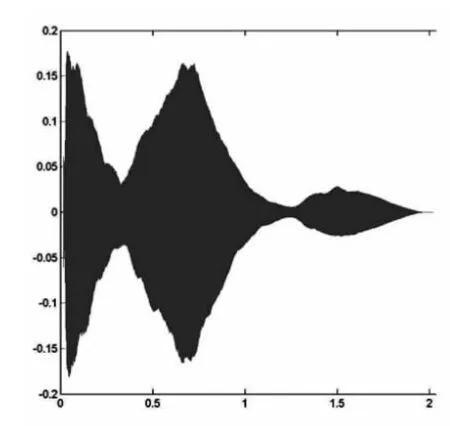
图1 信号的时域波形

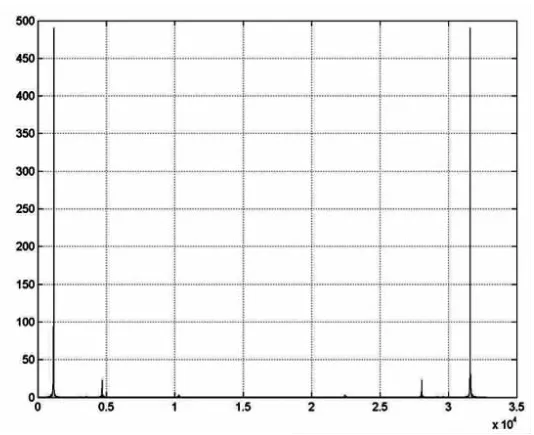
图2 信号频域的幅值

1.2 信号声音的重构

分析知道了该声波的频谱，接下来就可以得到它的时域值。当然可以使用傅立叶反变换，但在本例中将利用刚才分析的两个主要的频率成分来重构，执行下面的语句：

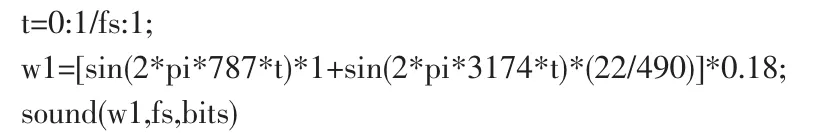
由于没有考虑相位和其他的频谱分量，所以波形和原来的波形相差较大，但大体的频谱是没有错的，通过听一下重构的声波，可以证实这一点。

2 wav文件的分段傅里叶分析

前面介绍了对wav文件直接进行一次性傅里叶变换的分析，但存在两个问题：第一，对分析的wav文件直接一次性做FFT，点数太大，而实际运用中DSP的FFT的点数是有限的，一般只能达到千点；第二，语音是分音节的，应该对它分段分析，所以下面引入分段处理数据，并连接每个段的频域结果。仍以前面讨论的“ding.wav”为例，进行分段傅里叶分析。

首先我们通过执行以下语句来显示wav文件的时域波形：

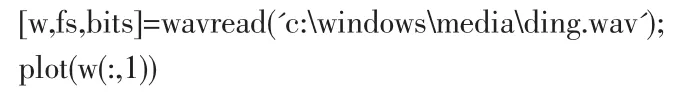
结果是显示的波形与图1一样。

接下来我们作1024点的分段FFT，通过执行以下语句来实现：

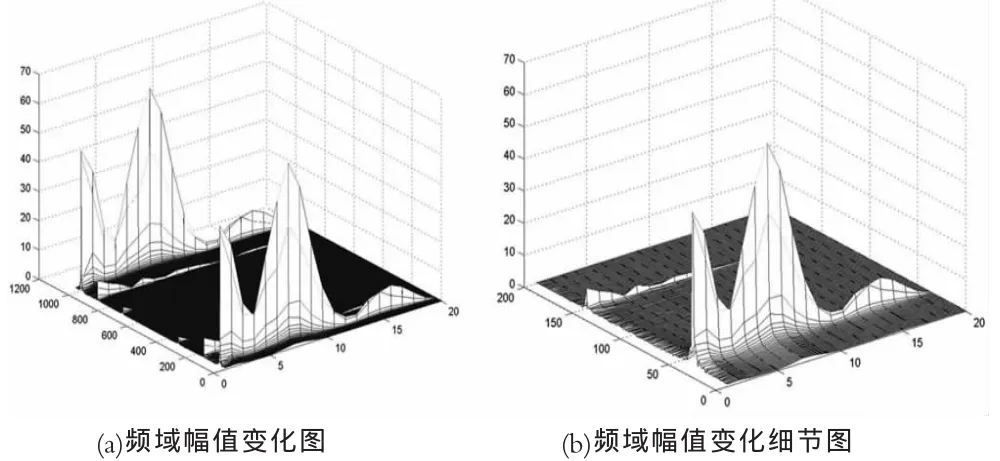
图3 分段后频域幅值变化图

运行结果如图3所示。x坐标表示段数，y坐标表示每段的点数，z坐标表示幅值大小。图3(a)每段1024点的频域幅值变化情况，可以看出它是以y=1024/2=512为对称的。为了更清楚地看到频域幅值变化的细节情况，图3(b)给出了每段200个点的波形。可以清楚地看到，首先沿y方向，整个wav数据分成的19个段中，每一段都有两个峰值，但幅度相差较大，该结果与图示一致的。再沿x方向看，分成的19个段中同一y位置的波形峰值幅度也是不一样的，呈波浪起伏变化，这也说明语音是分音节的。

下面做的是将图形中的两个主要谱线合成，执行下面的语句：

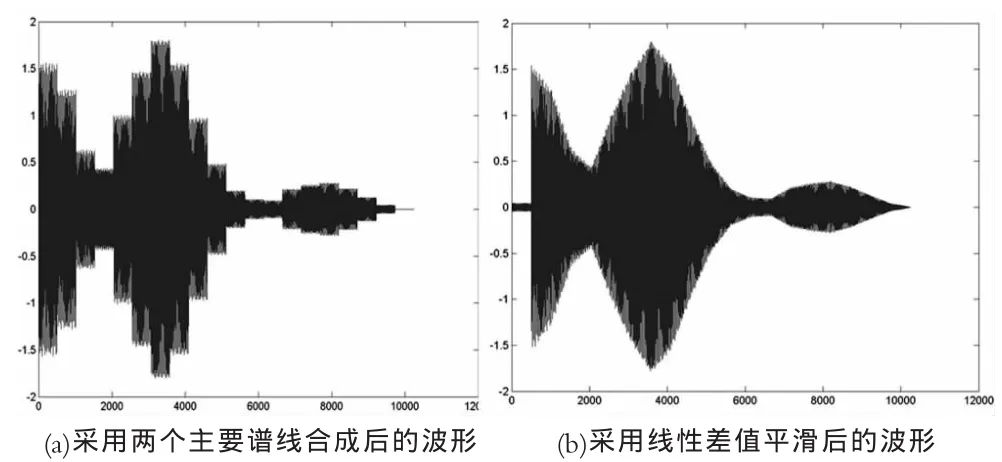
图4 合成波形及线性差值平滑波形

画出两个主要谱线合成后的波形，如图4(a)所示，并听听声音。

此时的声音听起来很刺耳，而且分辨不出原来的语音，但是可以感受到其音高的变化了。接下来用线性差值来平滑波形，得到的波形如图4(b)所示，执行下面的语句并听声音：

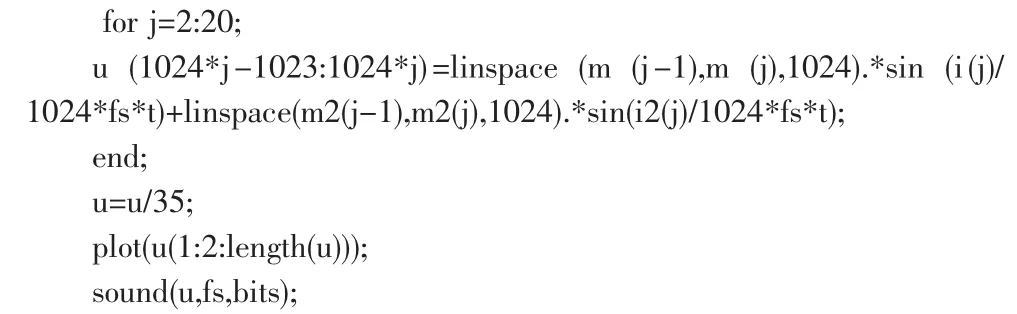
这时的声音柔和了一些，但还是分辨不出原来的声音。合成的声音和原来的声音的区别主要在于这里只是抽取了峰值，没有考虑峰值边上的波的形状，也没有考虑相位的关系。但如果把它们全部考虑进去，这就要用到傅里叶反变换(IFFT)，所以继续进行分析和合成，执行下面的语句：

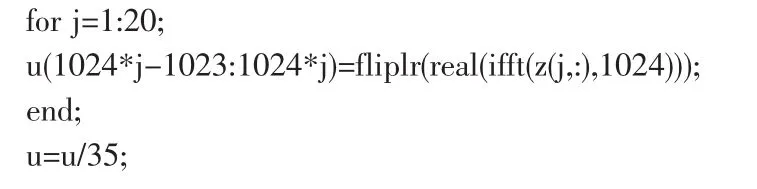
所得波形如图5所示，可见波形和原始波形一致，这时听到的声音和原来的声音就相同了。

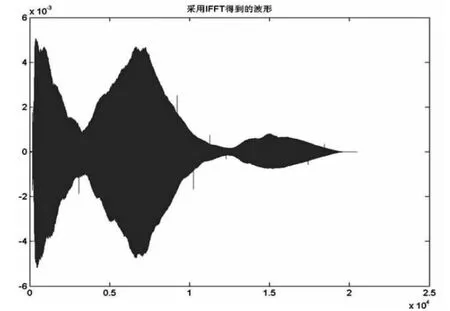
图5 采用傅里叶变换得到的波形

3 结语

以上通过引入简单的wav文件作为分析对象，以Matlab及快速傅里叶变换为分析工具，简要介绍了应用数字信号处理技术对wav信号文件进行分析的方法。可以预见，随着计算机技术、数字信号处理技术和大规模集成电路的迅速发展，数字信号处理的进步将在信号分析处理中得到更为广泛的应用。

[1]王艳芬.快速傅里叶变换信号分析实例[M].人民邮电出版社.

[2]曹弋.MATLAB 教程[M].机械工业出版社.