电磁波完全极化研究
2013-11-10党晓江李政杰
党晓江,李政杰,田 波
(空军工程大学防空反导学院,西安 710051)
0 引言
作为矢量波共有的一种性质,极化是指用一个场矢量来描述空间某一个固定点所观测到的矢量波随时间变化的特性。对电磁波而言,极化描述了电场矢端随时间变化的空间轨迹,表明了电场强度的取向和幅度随时间变化的性质。工程应用中的电磁波其极化形式多样,不仅有单一极化形式的椭圆极化波、圆极化波、线极化波,更多的是具有统计特性的复合极化形式波。通常把在观测期间电场矢端轨迹不变的极化形式称作完全极化形式电磁波,它是研究复合极化形式波的基础[1,2]。
通过大量查阅文献资料,发现对电磁波极化状态的研究还不够完善,主要有:对椭圆极化波方程的推导过于复杂[3~7];没有指出或部分提及[6]电磁波参数和极化椭圆参数的本质关系,且未在图形中直观地表示出来;对极化方向的判定标准各异并且判定结果有误[4,7]等。针对以上问题,本文一一作了详细的证明和阐述,结论对理论的进一步研究和工程应用有更好的指导作用。
1 三种极化波
假定电磁波为均匀平面波,传播媒质为自由空间,电磁波沿着三维直角坐标系中Z轴的正方向传播。设某种极化方式的电磁波的电场在水平方向(x轴)的分量为Ex,在垂直方向(y轴)的分量为Ey,其各自振幅和初始相位分别为EH与EV、φH和φV,则有

因为相位对电磁波的极化状态的影响只与相对相位有关而与绝对相位无关,为讨论简单,取φH-φV=φ,φH=0,z=0。即
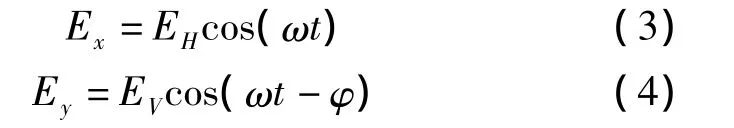
电场的正交分量Ex和Ey在各自的方向上以角频率ω作余弦振荡,合成矢量E在平面内旋转,如图1所示。
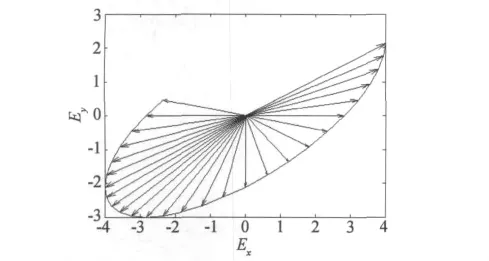
图1 3/4周期内合成矢量E在平面内旋转示意图
将此式(3)和式(4)的参数t消去,可得

这是一个椭圆方程,当 EH=4,EV=3,φ=π/4,极化椭圆如图2所示。

图2φ=π/4、EH=4、EV=3极化椭圆
上面得到的极化椭圆可以看成是椭圆x2/a2+y2/b2=1沿逆时针方向旋转τ角度得到。设(ξ1,η1)是该标准椭圆上的一点,(ξ2,η2)是该点旋转后的坐标,线性变换的矩阵为,即有
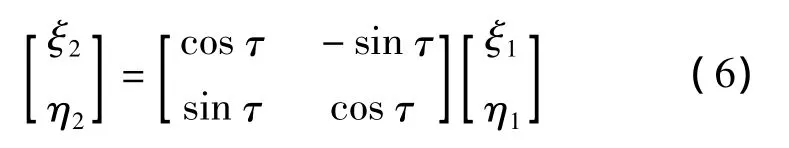
两边左乘线性变换的逆矩阵得
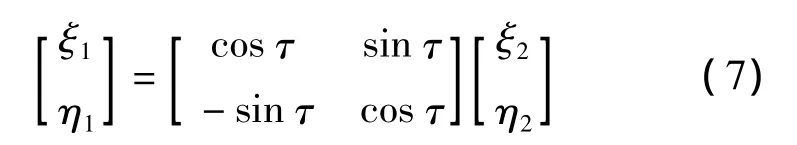
转置后为
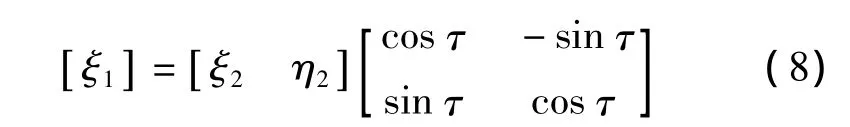
将x2/a2+y2/b2=1写成矩阵的形式
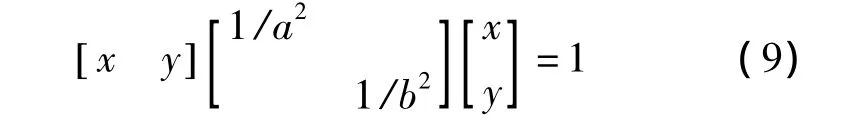
点(ξ1,η1)满足式(9),代入、化简并考虑到(ξ2,η2)具有一般性,得旋转后的椭圆方程
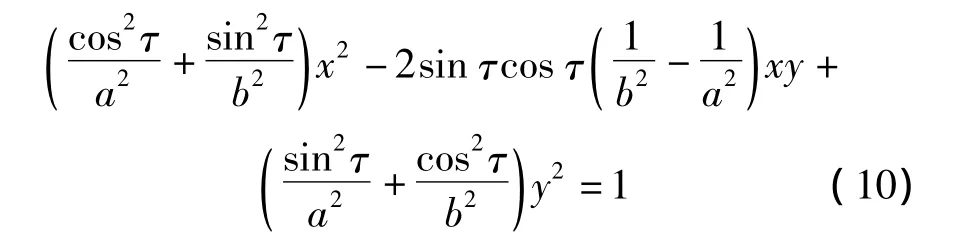
比较式(5)和式(10)得如下方程组

经过解方程,可得
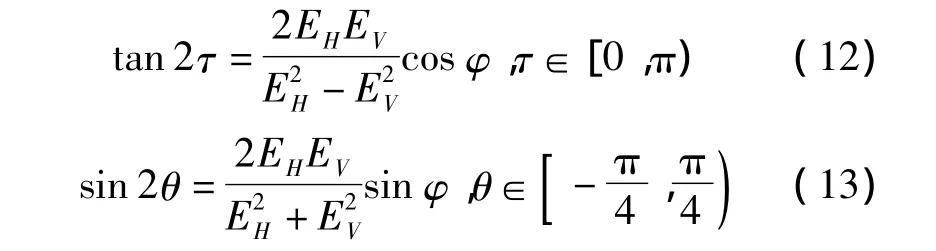
其中θ=arctan b/a,称为椭圆率角。
从极化椭圆方程可以看出,电场矢端的轨迹与电磁波的幅度参数EH与EV和相对相位参数φ有关。下面讨论两种特殊的椭圆极化波:线极化波和圆极化波。
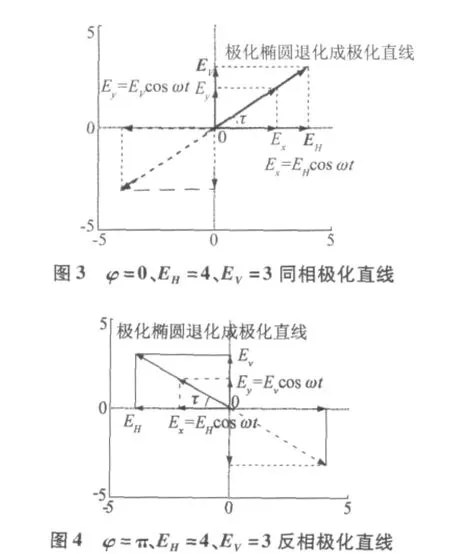
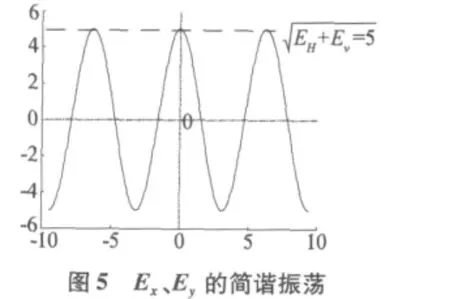
当约束条件为φ=kπ(k=0,±1,±2,±3…)即Ex与Ey同相或反相时,由参数方程可知Ey/Ex=±EV/EH=tan τ,在电磁波传播方向的某一点如z=0处,电场矢端的轨迹如图3、图4所示。
电场E在水平和垂直方向的分量Ex和Ey在各自的方向上以振幅EH和EV按余弦规律振动,E在直线y=(EV/EH)x和直线y=-(EV/EH)x上以振幅按照余弦规律振动。
当约束条件为 EH=EV=Em,φ=(2k+1)π/2(k=0,±1,±2,±3…)即Ex和Ey的相位相差±π/2时,由参数方程可知
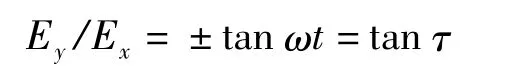
式(5)可以化简为

这是以Em为半径的圆的方程。
与电磁波传播方向垂直的横截面上如z=0处,此时电场矢端的轨迹如图6所示。
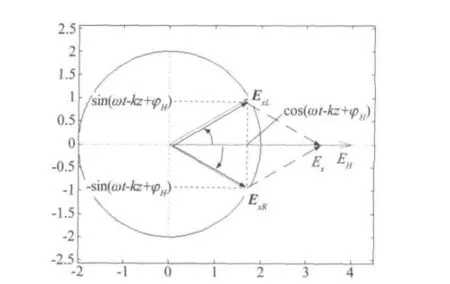
图6φ=±π/2时,极化椭圆退化为极化圆
2 三种极化波的解、合关系
以上间接地证明了在一组正交基下,两正交场分量的合成场为椭圆,并且这个过程是互逆的,即一椭圆极化可以分解成振幅不等的两线极化,特别当相位差满足特定条件时,可直接得出两正交场分量与圆极化和线极化的解、合关系,为了理论的完备性,下面证明椭圆极化与圆极化的解、合关系。
由可逆性可知,极化椭圆可以分解成水平垂直正交基下的一组分量:
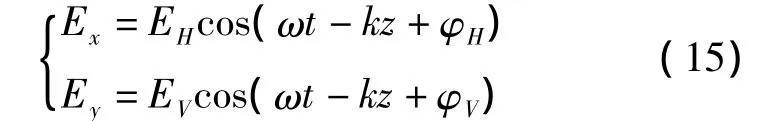
将水平分量Ex进行简单变换

可以看出,式(16)第一部分矢端轨迹为半径0.5EH的左旋的圆,用ExL表示,第二部分为同半径旋向相反的圆,用ExR表示,如图7所示。

图7 水平极化分量分解成两振幅相等旋向相反的圆极化波
将垂直分量Ey进行类似变换

式(17)第一部分矢端轨迹为半径0.5EV的右旋的圆,用EyL表示,第二部分为同半径旋向相反的圆,用EyR表示,如图8所示。
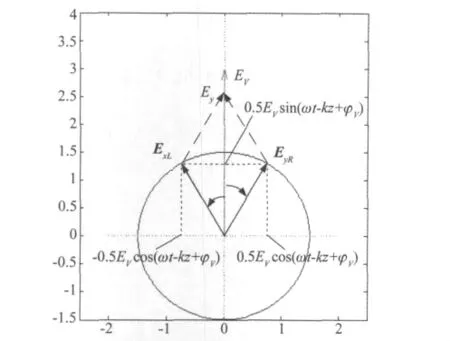
图8 垂直极化分量分解成两振幅相等旋向相反的圆极化波
这就说明,一个线极化波可以分解成两个振幅相等旋向相反的圆极化波,而一个椭圆极化波可以分解成两个振幅不等的线极化波,故一个椭圆极化波可以分解成两组振幅相等且旋向相反的四个圆极化波。
3 极化椭圆参数与电磁波参数的关系
极化椭圆的倾角τ呈现出椭圆的姿态,椭圆率角θ反映出极化椭圆的胖瘦(长轴和短轴的相对关系),电磁波的参数EH、EV表示在水平、垂直正交基下的电场分量幅度,联合则反映出电场的能量强度,φH和φV表示各自分量的绝对相位,联合则反映出相对相位。
令η=arctan(EV)/(EH),φ=φH-φV
则有
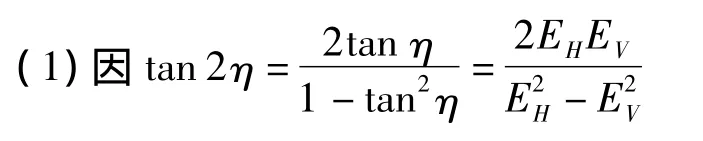
由式(12)可得
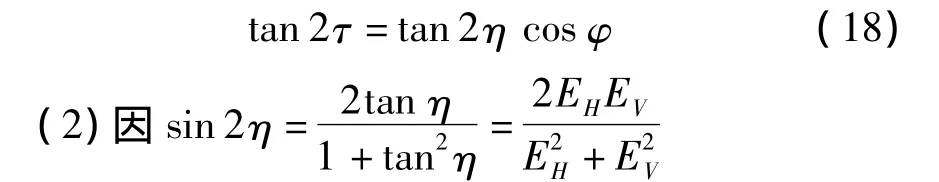
由式(13)可得
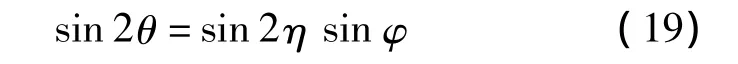
从式(18)和式(19)可以看出,极化椭圆可由极化电波的参数来确定。
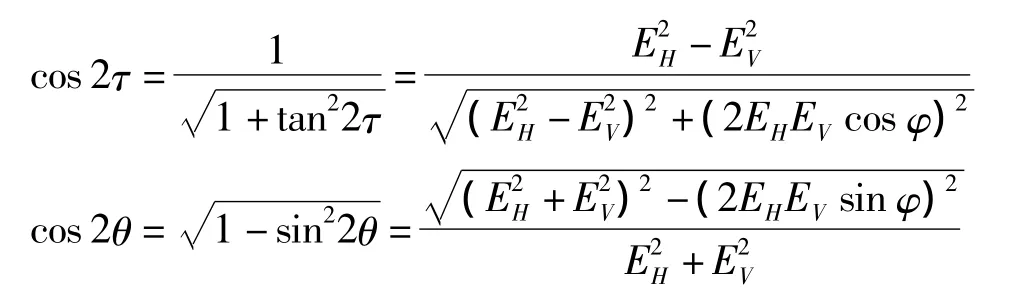
又经化简可知

所以有
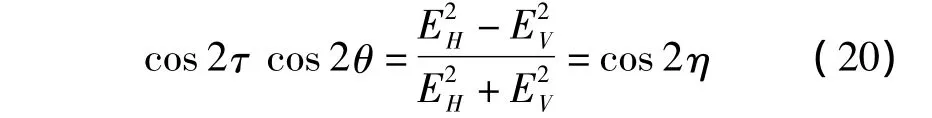
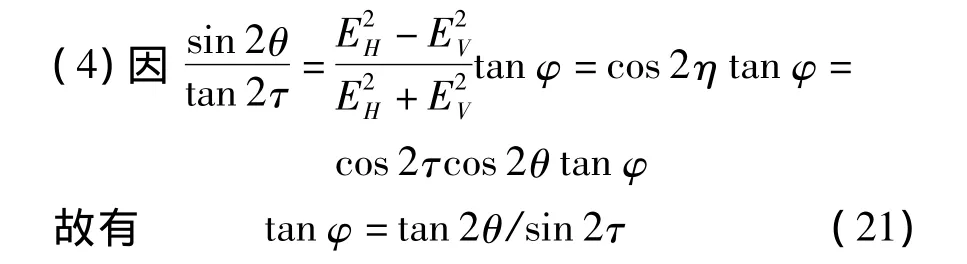
从式(20)和式(21)可以看出,极化电波可以由极化椭圆的参数来确定。
基于以上理论关系,可以在图形中直观的表示出椭圆姿态随电波参数变化情况,如图9所示。

图9 相对相位对极化椭圆姿态的影响
从图中可以看出,当相对相位φ从0到π变化时,不仅极化椭圆的姿态(倾角τ从arctan EV/EH减小到-arctan EV/EH)发生变化,而且还经历了由瘦变胖再变瘦的过程(椭圆率角θ从0增到到arctan EV/EH再减小到0)。特别地,φ=0或φ=π时,极化椭圆退化为极化直线,φ=π/2时,椭圆长轴与水平轴重合,其椭圆方程为标准椭圆方程,若此时EH=EV,则极化椭圆退化为极化圆,这与前面的论述一致。还需说明,φ从0到-π变化时,椭圆的姿态变化与上述一致。
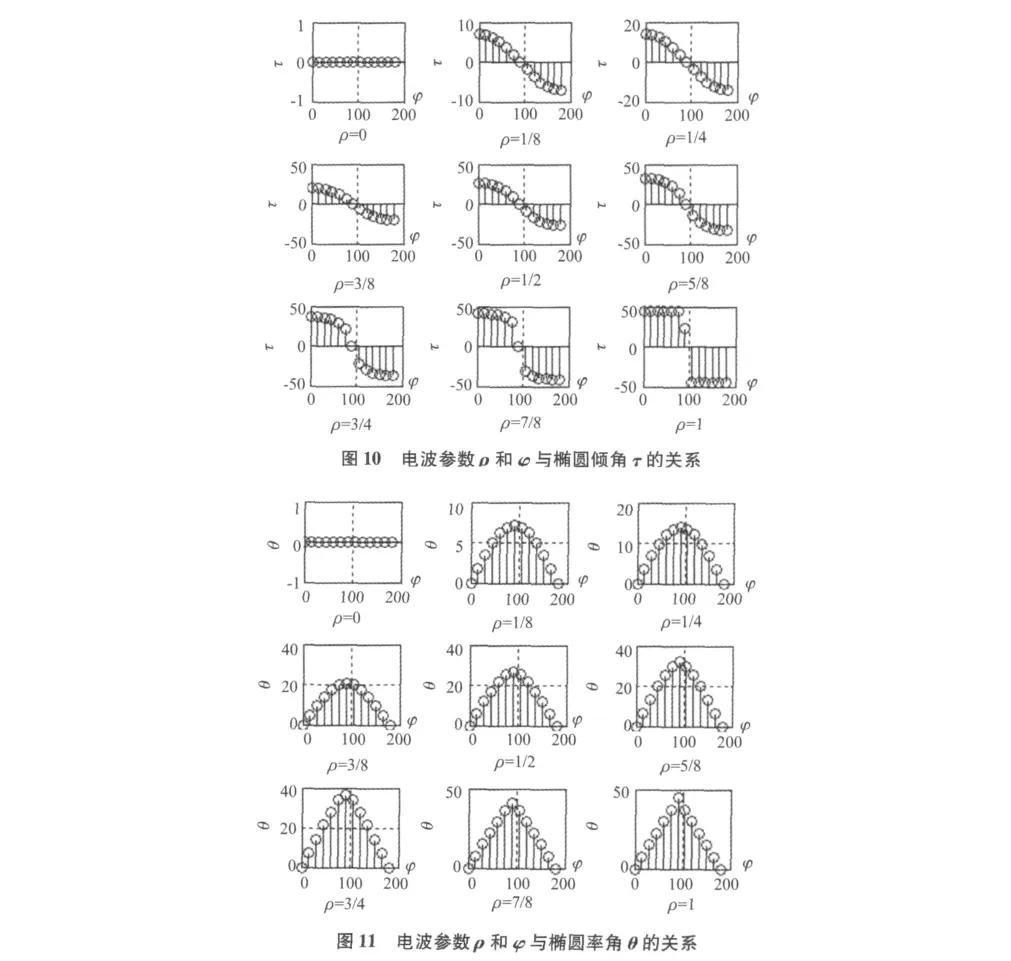
令ρ=tan η,则可得到电波参数ρ和φ与椭圆τ和θ的确定关系,如图10、图11所示。
4 极化方向
以上讨论了极化波的幅度随时间变化的性质,不仅如此,极化波的方向也随时间的变化而变化。沿电磁波传播的方向看去,若电场指向沿顺时针方向旋转,称之为右旋极化波,否则为左旋极化波。由于椭圆极化波具有普适性,线极化波和圆极化波都是其退化的特例,因此先从椭圆极化波取向的讨论入手。
极化椭圆的旋转问题可以转化为其斜率随时间变化的问题。由极化椭圆参数方程可得
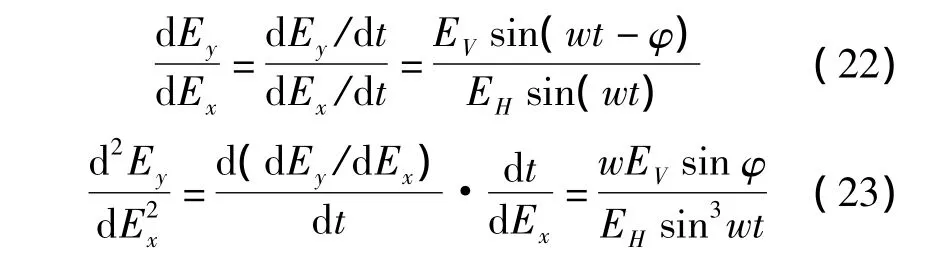
通过证明,在一个周期内椭圆的斜率的走势情况只与φ的正负有关,其他的参数只影响斜率变化的细节。在这里将旋转周期归为2,当φ>0时,d2Ey/dE2x在的值在(-1,0)∪(0,1)上恒为正,表明dEy/dEx单调递增,且在 -1、0-、0+、1 处分别取得-∞、+∞、-∞、+∞,即电场矢端左旋。同理,当φ <0时,d2Ey/dE2x在的值在(-1,0)∪(0,1)上恒为负,表明 dEy/dEx单调递减,且在 -1、0-、0+、1处分别取得 +∞、-∞、+∞、-∞,即电场矢端右旋。
现将φ取0到π以及0到-π之间的离散值,仿真结果如图12和图13所示。
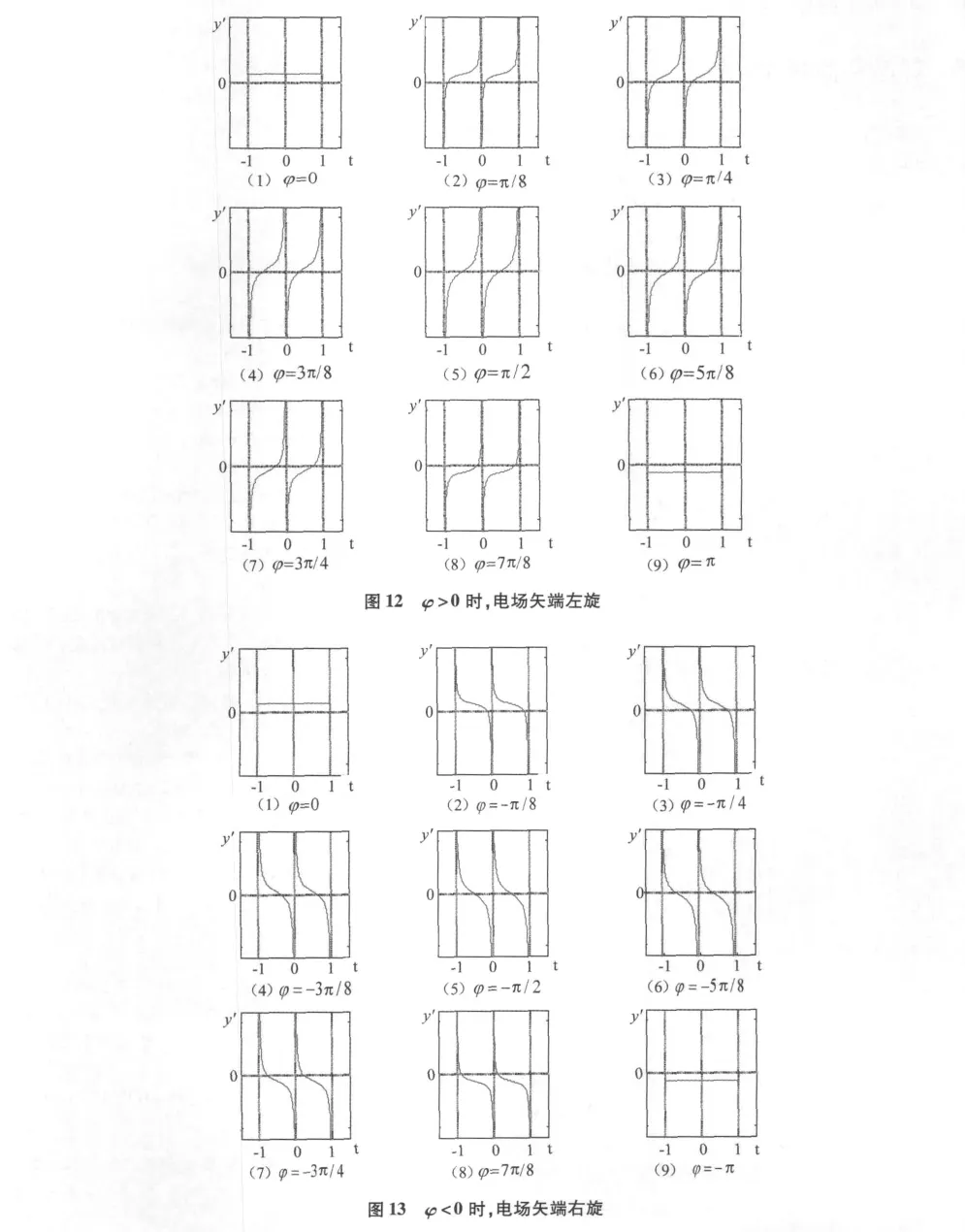
比较两图可以看出φ的正负决定矢端的旋转方向,在每一幅图中,关于π/2或-π/2对称的φ值对应椭圆的斜率的变化率是相同的,如图4和图6、图3和图7、图2和图8,以及图1和图9。特别地,当φ=0时,椭圆极化为线极化,其斜率是恒值,图1和图9正说明了这种现象。
5 静态空间极化
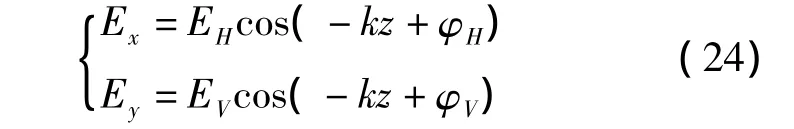
这是一个关于传播路径z的椭圆螺旋方程,如当EH=4,EV=3,φ=φH-φV=π/3其三维视图如图14所示。在与传播路径垂直的xy平面内的投影就是如图15所示的极化椭圆。
当时间t处于某一个时刻如t=0,式(1)和式(2)可化为
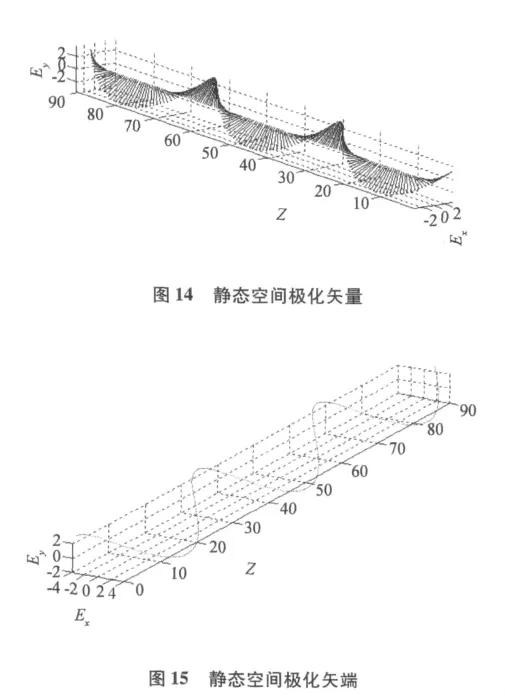
值得注意的是,静态空间极化螺旋线的旋向与极化方向恰好相反,如图15当φ=π/3时螺旋方向为顺时针,而由极化方向的结论可知,当φ>0时,极化方向为左。另一方面这是由横波的传播特性决定的。
6 结语
本文从最普适的椭圆极化形式入手,导出了两种退化的极化形式:线极化和圆极化;阐明了三种极化波的解、合关系;推导了极化椭圆的参数τ和θ与电磁波参数η和φ的关系;证明了极化方向与电磁波在水平垂直极化基下两分量相对相位φ的关系以及静态空间极化,结论对理论的进一步研究和工程应用有更好的指导作用。
[1]李锦屏,高继森,孙春霞.电磁场与电磁波[M].兰州:兰州大学出版社,2007.
[2]牛中奇,等.电磁场理论基础[M].北京:电子工业出版社,2001.
[3]伍刚,张小平.基于电磁波极化合成与分解的研究[J].攀枝花学院学报(综合版),2008,25(3):76-79.
[4]刘军民,林相波.平面电磁波极化方式的分析与判断[J].电气电子教学学报,2011,33(1):95-97,110.
[5]KONG J AU.Electromagnetic wave theory[M].Bejing:Higher Education Press,2002.
[6]梁昌洪,陈曦.电磁波极化及其应用[J].电气电子教学学报,2011,33(3):1-5.
[7]王被德.电磁波的极化及其应用[J].电波科学学报,1999,14(3):347-356.
[8]程云鹏.矩阵论[M].西安:西北工业大学出版社,2005.
[9]曾清平,等.雷达极化技术与极化信息应用[M].北京:国防工业出版社,2006.
[10]李永祯,肖顺平,王雪松,等.雷达极化抗干扰技术[M].北京:国防工业出版社,2010.
[11]孙彬,李永祯,王国玉,等.基于最佳检测的雷达发射-接收极化联合优化方法[J].宇航学报,2012,33(4):460-464.
[12]李军,李金梁,王涛,等.距离扩展目标极化检测的比较研究[J].信号处理,2010,26(2):213-218.
[13]刘勇,戴幻尧,李永祯,等.有源压制干扰背景下的雷达目标空域极化检测[J].电波科学学报,2010(3):453-459.
