软土地区深基坑支护方案优选模型研究及应用★

彭文柏

(云南省建筑科学研究院，云南昆明 650223)

0 引言

深基坑工程系统是一个综合性的岩土工程问题，在基坑开挖过程中，支护方案选择的好坏直接关系到整个工程的成败［1，2］。由于深基坑工程具有区域性强、造价高、发生事故后果严重等特点，使得基坑支护方案必须科学合理、安全可靠、方便可行、造价经济。因此，如何科学有效地进行基坑支护方案的优选显得尤为重要。

深基坑支护方案的优选是根据某一深基坑工程所要达到的目标，从众多可行方案中选出一个最佳方案，本质上是对多种方案下多目标的评价与选择。目前，相关专家学者针对基坑支护方案优选开展了深入研究，提出了一系列不同的基坑支护方案优选方法，取得了一定的研究成果，归纳如下:王广月等［1］根据评价指标的模糊性及评价方案的层次性，采用模糊数学理论和层次分析理论，建立基坑支护方案的优选模型。张尚根、陈灿寿等［2］根据评价指标的模糊性，采用模糊数学理论建立了优选模型。阮永芬、叶燎原［3］根据各指标的信息不完全性及相互关联性，采用灰色系统理论对方案进行优选。冯玉国、王渭明［4］根据评价指标的不相容性，提出基于灰色物源分析的优选模型。冯庆高、周传波等［6］提出了灰色模糊可变决策法。梅年峰、罗学东、蒋楠等［8］提出了灰色多目标决策模型进行基坑支护方案优选。

鉴于此，通过调查研究以昆明为例的软土地区工程地质特征，明确影响软土地区深基坑方案优选的因素，建立了一套多层次、多目标基坑支护方案综合评价指标体系，在此基础上，运用灰色关联分析法选取最优的基坑支护方案。

1 灰色系统理论计算原理

1.1 灰色关联法基本思想

灰关联法的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近，相应序列之间的灰关联度就越大，反之越小。简而言之，灰色关联分析法就是通过计算系统特征变量数据序列与相关因素变量数据序列之间的关联度，建立灰关联矩阵，利用优势分析原则，得出各影响因素的顺序，以确定主要影响因素［8］。

设灰色系统有n个灰色因子数列，即:

如果要以其中任意的一组数列Xj为母序列(参考序列)来分别计算序列Xi，i≠j，相对于Xj(i)之间的关联度、关联序以及关联矩阵。

1.2 灰色关联法计算步骤

1)进行原始数据变换。

为了使各数列间具有统一的量纲，需要对数据进行预处理。原始数据预处理有多种方式主要包括:

a.初值化变化。

b.均值化变换。

4)求Xi对各数列每个时刻的关联系数ξ(ij)(k)。

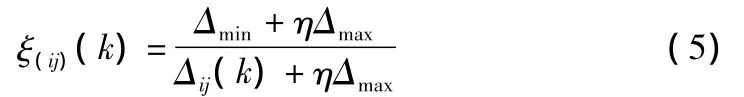
其中，η∈［0，1］，一般可取0.5。

5)计算各数序列对Xj的关联度。

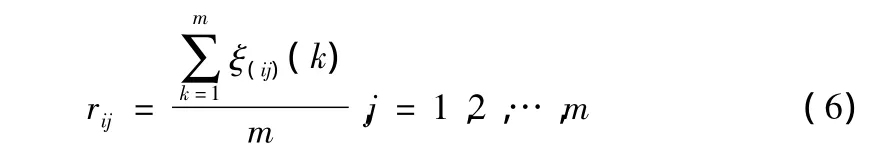
2 软土地区深基坑支护综合评价指标体系的构建

依据软土地区城市建筑密集的特点，基坑支护方案的选择不仅要考虑方案的安全可行性和经济合理性，同时需考虑基坑工程对周围环境的影响以及施工便捷性。因此合理构建深基坑支护评价指标体系应考虑的因素主要包括:基坑支护设计方案的科学、合理，直接关系到基坑支护安全;基坑支护对周围环境产生的影响则包括降水引起地面沉降、侧向变形等;施工方案便捷性影响施工工期、施工难易程度等;方案经济合理性体现在工程造价和工程失效的经济损失。

根据昆明软土地区深基坑工程建设实际特点、周边环境、工程地质条件等，从安全可行性、环境保护、施工便捷性、经济合理性4个方面构建基坑支护方案多层次多目标评价指标体系，主要由4 个一级指标(B1，B2，B3，B4)和 12 个二级指标(C1，C2，C3，C4，C5，C6，C7，C8，C9，C10，C11，C12)组成，参见图1。

图1 深基坑支护方案评价指标体系

3 工程实例分析

3.1 工程概况

昆明市软土区域地质是内陆断陷盆地型软土的一个典型代表，随着深大基坑工程建设不断涌现，软土地质特征对深基坑工程的影响日趋明显。昆明软土区域形成的地质背景较为特殊，濒临滇池水体，是典型的高原断陷盆地型软土。

昆明拟建某安置小区，占地总面积约19 850 m2，基坑开挖深度约为5.2 m～7.5 m。该建筑物共设2层地下室。现场为拆除旧房场地，场地北侧有3层高的建筑，距离基坑约为6.5 m，南侧则有护城河，东侧为光大银行6层建筑，距基坑9 m左右，西侧为环城西路。基坑开挖影响的土层为杂填土、粉质粘土、淤泥、粉质粘土、中粗砂，土层的物理力学性质见表1，开挖土层为杂填土、粉质粘土、淤泥，基坑开挖后整体稳定性较差，需要对其进行支护，且基坑开挖范围内土层含水性和透水性较差，需要采取有效地止水措施。

根据基坑工程的特点、场地的工程地质条件、相关的施工经验等，初步考虑三种基坑支护方案:排桩+内支撑+单排深层搅拌桩防渗幕墙(A1)、排桩+锚杆+单排深层搅拌桩防渗幕墙(A2)、地下连续墙+内支撑(A3)。

表1 土层的物理力学性质

3.2 确定理想方案的指标期望值

按照上述的基坑支护方案评价指标体系，邀请10名专家对备选方案及理想方案的各个指标进行逻辑推理评语评价，进而确定备选方案和理想方案的各指标期望值，相关数据见表2。

3.3 基于灰关联系统的最优方案评价

运用DPS灰关联模型，分别从一级指标、二级指标、一二级综合指标作为计算参数三个方面计算备选方案与理想方案的关联度。其中原始数据采用均值化变换，分辨系数ρ取0.5。综合分析比较而确定最优的方案。

1)以一级指标为计算参数，其计算的结果(指标均值变换、关联矩阵)见表3，表4。

表2 专家对备选方案和理想方案指标的评价表(一、二级指标)

表3 一级指标关联系数矩阵

表4 一级指标方案的综合关联度

根据表4可知γ1＞γ2＞γ3，则由一级指标可确定A1方案为最优支护方案。

2)以二级指标为计算参数，其计算的结果(指标均值变换、关联矩阵)见表5，表6。

根据表6可知γ1＞γ2＞γ3，则由二级指标综合关联度可确定A1方案为最优支护方案。

综上两种不同的最优支护方案的方法，均获得结果为γ1＞γ2＞γ3，因此，第一种方案即排桩支护+内支撑+单排深层搅拌桩防渗幕墙A1为最优方案。该方案为实际工程采纳，实际运用效果良好。

表5 二级指标关联系数矩阵

4 结语

1)以昆明拟建某安置小区深基坑工程为例，依据软土地区工程的地质特点，从安全可行性、环境保护、施工便捷性、经济合理性等4个方面构建了适用于软土地区深基坑支护方案的多层次、多目标综合评价指标体系，主要是由4个一级指标和12个二级指标组成。

表6 二级指标方案的综合关联度

2)基于灰色关联方法，分别以一级指标、二级指标为计算参数，分析两种不同情况下备选方案与理想方案的综合关联度，以此对基坑支护方案进行优选。高级指标从整体范围上对支护方案进行评价，低级指标则考虑到具体的影响因素，两者有各自的优缺点，从不同层面分别考虑，可达到相互印证的效果，为方案优选提供了充分的参考依据。工程实例研究表明，该方法科学合理、简单易行，与工程实际情况吻合，实施效果良好，具有一定的推广和应用价值。

［1］王广月，刘 健，芮洪范.深基坑支护方案的模糊物元评价方法［J］.山东大学学报，2004，34(2):84-88.

［2］张尚根，陈灿寿，夏 炎.深基坑支护方案的模糊优选模型及其应用［J］.岩石力学与工程学报，2004，23(12):2046-2048.

［3］阮永芬，叶燎原.用灰色系统理论与方法确定深基坑支护方案［J］.岩石力学与工程学报，2003，22(7):1203-1206.

［4］冯玉国，王渭明.深基坑支护方案灰色物元分析优化模型及其应用［J］.岩土力学，2009，30(8):2467-2470.

［5］杨晓强.某基坑支护方案的设计优化［J］.山西建筑，2012，38(3):71-72.

［6］冯庆高，周传波，傅志峰，等.基坑支护方案的灰色模糊可变决策模型［J］.岩土力学，2010，31(7):2226-2231.

［7］魏新江，余 银，张世民.基于模糊灰关联投影法的深基坑支护方案优选［J］.岩土力学，2011，32(S1):438-444.

［8］梅年峰，罗学东，蒋 楠，等.基坑支护方案灰色多目标决策优选模型的建立与应用［J］.中南大学学报(自然科学版)，2013，44(5):1982-1987.

［9］邓聚龙.灰色系统基本方法［M］.武汉:华中科技大学出版社，2002:65-69.