基于用户语义相似性的协同过滤推荐算法

李 想，周 良

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

协同过滤推荐是当前应用最广泛、最成功的个性化推荐技术。协同过滤推荐主要根据用户对项目的评分数据，发现用户之间或者项目之间的相关性，预测目标用户对未评分项目的喜好程度，从而产生推荐。目前常用的协同过滤推荐算法主要分为2类:基于用户的协同过滤推荐和基于项目的协同过滤推荐[1]。

传统的基于用户的协同过滤推荐算法是以用户－项目评分矩阵为基础来计算用户之间的相似性，用户评分数据的缺失使系统难以准确定位目标用户的最近邻，从而导致推荐质量下降。近些年，一些研究者开始尝试将语义知识应用到协同过滤推荐中，在解决评分数据稀疏性问题上取得了显著的效果。文献[2]提出了一种基于项目语义相似度的协同过滤推荐算法，通过计算项目之间的语义相似性来预测用户评分，并填充用户评分矩阵，再计算用户的相似性进行推荐。文献[3]提出了一种基于本体用户模型的个性化推荐算法，利用本体构建用户兴趣模型，并通过改进的相似度计算方法来计算用户相似度。文献[4]提出了一种领域知识驱动的协同过滤推荐算法，通过项目语义相似度计算用户之间的语义相似度，同时结合用户评分相似性和用户语义相似性计算用户最近邻，有效地改善了推荐质量。

本文提出了一种基于用户语义相似性的协同过滤推荐算法。其核心在于利用领域本体中概念之间的关系来描述项目之间的语义关系，同时利用语义扩展的余弦相似性方法来改进传统的用户相似性度量方法，并以此来计算用户语义相似性。该算法能够很好地克服协同过滤中数据稀疏性导致的推荐质量下降的问题，提高推荐的准确性。

1 基于用户语义相似性的协同过滤推荐流程

协同过滤推荐根据目标用户最近邻居集的偏好来预测目标用户的偏好，推荐流程主要分为2个部分:发现用户最近邻和产生推荐。基于用户语义相似性的协同过滤推荐通过引入语义知识，同时综合用户评分数据来计算用户语义相似度，推荐流程如图1所示。

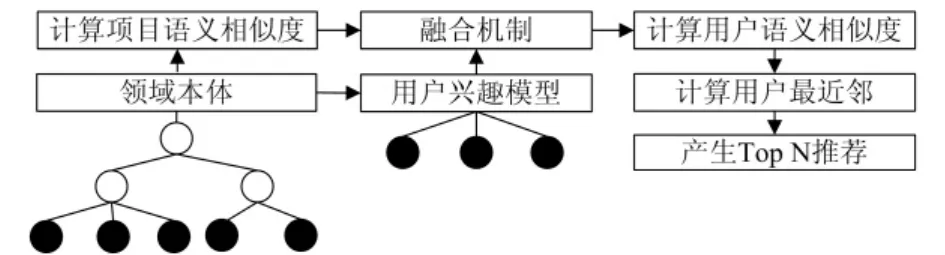
图1 基于用户语义相似性的协同过滤推荐流程图

根据图1中描述的推荐流程，首先利用项目的分类信息构建领域本体，收集用户兴趣信息并构建用户兴趣模型，用户兴趣模型由分类本体树中的叶子节点和相应的评分组成;然后，根据领域本体内部的语义关系计算项目之间的语义相似度，综合项目语义相似度和用户评分数据来对余弦相似性方法进行语义扩展，以此来计算用户语义相似度，并为目标用户产生最近邻居集;最后，根据用户最近邻居集的评分产生Top N推荐。

2 基于用户语义相似性的协同过滤推荐算法

2.1 计算项目语义相似度

领域本体通常用来描述某个领域内的概念以及概念之间的关系，领域本体中的上层概念是下层概念的泛化，下层概念是上层概念的具体化。项目之间语义关系的表达可以借助领域本体来实现，图2描述了电影领域的一个分类本体，领域本体树中的叶子节点表示具体的电影项目，非叶子节点表示泛化的电影分类概念。

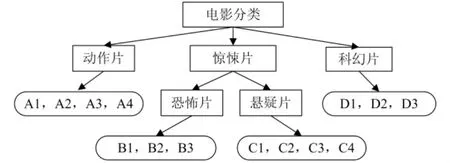
图2 电影领域的分类本体

根据Ganesan在文献[5]中提出的思想来计算项目之间的语义相似度。设分类本体树U中叶子节点的集合为 LLU={l1，l2，l3，…，ln}，LCAU(li，lj)表示叶节点li和lj的最近公共祖先节点，depth(l)表示从根节点到节点l的路径长度，叶节点li和lj的语义相似度定义为:

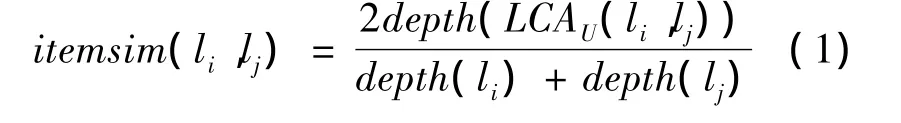
根据定义可知，itemsim(li，lj)∈[0，1]，当且仅当li=lj时，itemsim(li，lj)=1。任意两个项目之间的语义相似度可以根据公式(1)计算得到，且相似度随着最近公共祖先节点深度的增加而增加。

2.2 用户语义相似性度量方法

协同过滤算法的核心是计算用户之间的相似性，从而发现目标用户的最近邻。传统的相似性度量方法主要有3种:余弦相似性、相关相似性和修正的余弦相似性。传统的相似性度量方法过于依赖用户评分数据，在用户评分数据极端稀疏或者用户之间评分项目的交集较少的情况下，不能有效地度量用户之间的相似性，进而影响推荐质量。本文根据用户评分项目之间的语义相似性和用户对项目的评分，重新定义向量点积的计算方法，并利用语义扩展的余弦相似性方法来计算用户语义相似度。

设用户a和用户b评分过的项目数量分别为m和n，用户a和用户b的兴趣模型分别为n}。其中，pi和s(pi)分别为用户a评分过的项目及其相应的评分值，qj和s(qj)分别为用户b评分过的项目及其相应的评分值。将用户兴趣模型映射到向量空间上，同时考虑到用户评分尺度不同的问题，则用户a和用户b的兴趣评分向量Ia和Ib可以分别表示为:

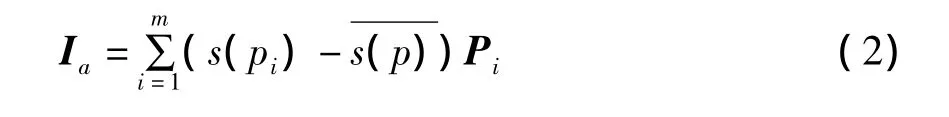
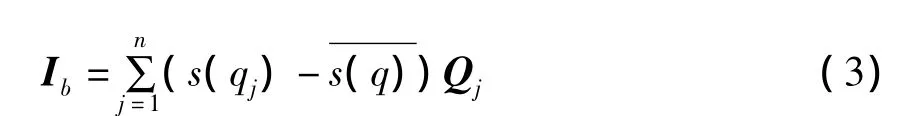
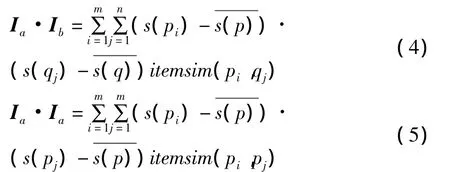
同理可以计算Ib·Ib，当用户a和用户b之间没有共同的评分项目时，依然可以利用公式(4)来计算得到一个非零数值。用户a和用户b的语义相似性可以利用经过语义扩展的余弦相似性方法来计算:

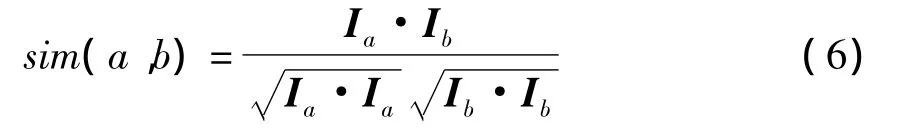
2.3 产生推荐

发现最近邻的目标就是为目标用户a产生一个最近邻居集合 Na={a1，a2，…，ak}，a ∉ Na，且sim(a，ai)≥sim(a，ai+1)，1≤i＜ k，则可以利用公式(7)来计算用户a对未评分项目i的预测评分Pa，i，然后选择预测评分值较高的若干项目推荐给目标用户a。

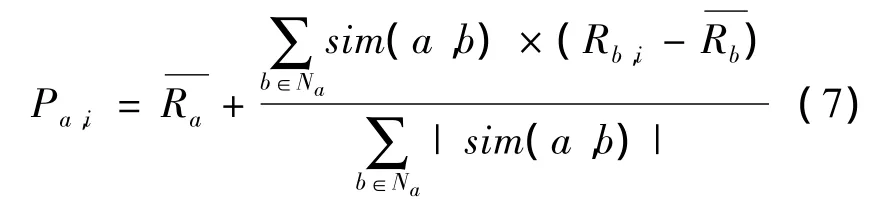
式中:sim(a，b)表示用户a与用户b之间的语义相似度;Rb，i表示用户b对项目i的评分;和分别表示用户a与用户b对项目的平均评分。

3 实验及分析

3.1 数据集

本文采用MovieLens站点提供的数据集对基于用户语义相似性的协同过滤推荐算法进行测试，并和传统的基于用户的协同过滤推荐算法进行实验对比。MovieLens数据集包含超过43000个用户对3500部电影的评分数据以及电影的分类信息。本文根据电影的分类信息构建电影领域的分类本体，从该数据集中随机选取5000条评分数据作为实验数据集，其中包含159个用户和614部电影，并将其分为训练集和测试集，训练集占80%，测试集占20%。该实验数据集的稀疏等级为:

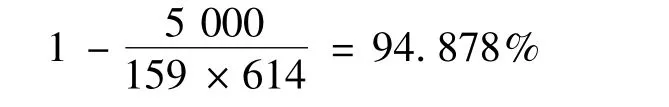
3.2 评价标准

本文采用平均绝对偏差MAE(Mean Absolute Error)作为算法质量的评价标准，它通过计算预测的用户评分和用户实际评分之间的偏差来衡量预测的准确性，MAE的值越小，算法推荐的质量越高。设用户评分的预测值集合为{p1，p2，…，pN}，其对应的实际的用户评分值集合为{q1，q2，…，qN}，则 MAE 的计算方法如下[6]:

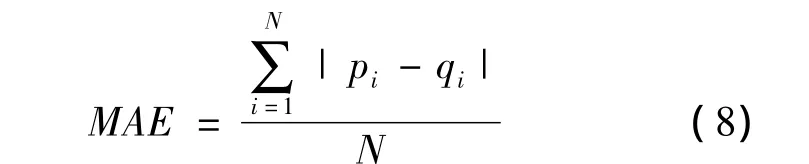
3.3 实验结果及分析

为了检验基于用户语义相似性的协同过滤推荐算法的有效性，将传统的基于用户的协同过滤推荐算法与之进行比较，用户邻居数从5不断增加到40，间隔为5。其中，传统的基于用户的协同过滤算法分别以相关相似性和余弦相似性来计算用户相似度，实验结果如图3所示。

从图3中可以看出，与传统的基于相关相似性和余弦相似性的协同过滤算法相比，本文提出的算法均有较小的MAE值。由此可知，与传统的基于用户的协同过滤推荐算法相比，基于用户语义相似性的协同过滤推荐算法在用户评分数据极端稀疏的情况下可以有效地提高推荐质量。

4 结束语

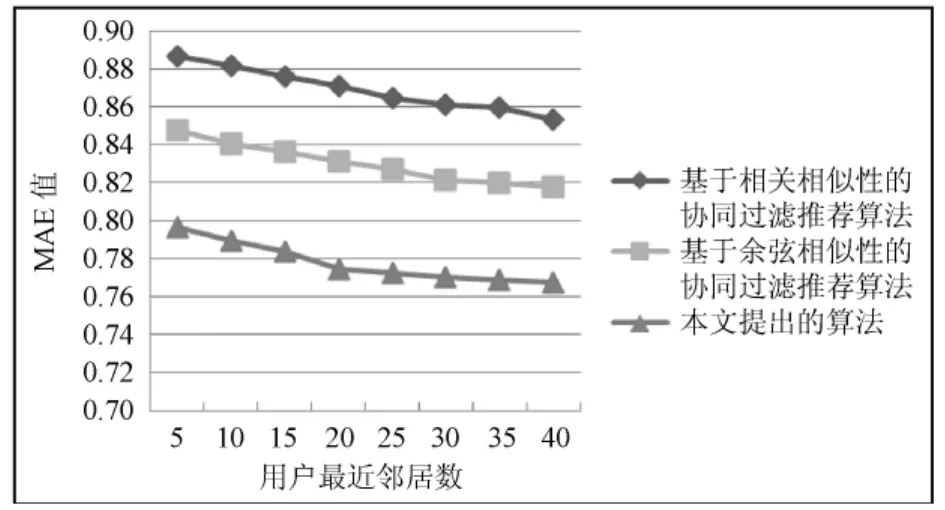
图3 几种协同过滤推荐算法比较

为了克服传统协同过滤推荐中存在的数据稀疏性问题，本文提出了一种基于用户语义相似性的协同过滤推荐算法。通过构建领域本体来描述项目之间的语义关系，并计算项目语义相似度，根据项目语义相似度和用户评分来对传统的余弦相似性公式进行语义扩展，计算用户语义相似度并寻找用户最近邻。通过实验证明，在用户评分数据极端稀疏的情况下，该算法与传统的协同过滤推荐算法相比显著地提高了推荐质量。

[1] 马宏伟，张光卫，李鹏.协同过滤推荐算法综述[J].小型微型计算机系统，2009，30(7):1282－1288.

[2] 肖敏，熊前兴.基于项目语义相似度的协同过滤推荐算法[J].武汉理工大学学报，2009，31(3):21－32.

[3] Jiangling Yuan，Hui Zhang，JiangFeng Ni.A new ontology－based user modeling method for personalized recommendation[C]//Computer Science and Information Technology(ICCSIT).Chengdu:20103rd IEEE International Conference，2010:363－367.

[4] Lingling Zhang，Xiaojie Zhang，Quan Chen，et al.Domain－Knowledge driven recommendation method and its application[C]//2011 Fourth International Joint Conference.Yunnan:Computational Sciences and Optimization(CSO)，2011:21－25.

[5] Ganesan P，Garcia－Molina H.Exploiting hierarchical domain structure to compute similarity[J].ACM Transactions on Information Systems，2003，21(1):64－93.

[6] 邓爱林，朱扬勇，施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报，2003，14(9):1621－1628.