Lindenbaum定理的新证明方法及其应用

万展翔，陈国龙，张 龙 (淮北师范大学数学科学学院，安徽 淮北 235000)

Lindenbaum定理的新证明方法及其应用

万展翔，陈国龙，张 龙 (淮北师范大学数学科学学院，安徽 淮北 235000)

模型论研究形式语言及其解释(模型)之间的关系，是形式语言的语法和语义的关系的理论。模型论的主要方法是构造模型。用新的模型论方法得到了几个相关结论，并且利用得到的结论证明了模型论中的Lindenbaum定理和高等代数中向量组极大线性无关组可以由任何一个线性无关组扩充的结论。

模型论方法；和谐理论；Lindenbaum定理；极大线性无关组

1 预备知识

定义1[1]由L中语句构成的任一集合Σ也称为L中的理论。如果L中每一公式都能由Σ推出，则称理论Σ是不和谐的，否则称Σ是和谐的，而L中任何真包括Σ的理论都不再是和谐的，则称Σ是极大和谐的。

引理1[1](广义完全性定理) 设T是L的和谐公式集(理论)，则T是可满足的，即T有模型。

引理2[2](可靠性定理) 设T是L的理论，α是一个语句，若T├α(T推出α)，则T╞α(α在T中是成立的或T满足α)。

引理3[1](紧致性定理)L中每一个理论T有模型当且仅当T的每一有限子集都有模型。

2 相关结论

定理1设T是L的一个理论，T不和谐当且仅当存在一个语句α，T├α且T├(┐α)(┐α表示非α)。

证明(⟹)。若T不和谐，显然有T├α且T├(┐α)。

(⟸)。设α是L的一个语句，且T├α且T├(┐α)。又由于对L中任意语句β，都有├(┐α)→(α→β)。进而有T├α→β，从而进一步有T├β。因此，T是不和谐的理论。

推论1设T是L的一个理论，如果对任何自然数n，T都有元数大于n的有限模型，则T有无限模型。

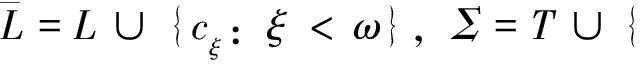
推论2设T是L的和谐理论， 是L的一个语句，①若T├α，则T∪{α}是L的和谐理论；②若T不能推出α，则T∪{┐α}是L的和谐理论。

证明①因T├α，故有T╞α。又T和谐，故T有模型A，即A╞T，从而A╞α。进而有A╞T∪{α}，因此，T∪{α}是L的和谐理论。②假设T∪{┐α}不和谐，从而T，┐α├α，由演绎定理有，T├(┐α)→α，注意到├(┐α→α)→α，进而有T├α这与题设条件T不能推出α矛盾，证毕。

推论3设T是L的一个和谐理论，则T├α当且仅当T╞α。

证明(⟹)。由引理2知T├α，则T╞α显然成立。

(⟸)。假设T不能推出 ,因T╞α，由条件知T有模型，且对T的任一模型A，都有A╞α。又T不能推出α，且T和谐，由推论2知T∪ {┐α}和谐，从而由引理1知T∪ {┐α}有模型B，即B╞T且B╞(┐α)，而由上述讨论知B╞α，矛盾。

推论4设Th(A)={α：A╞α}，A为L的一个模型，则Th(A)是一个极大和谐的理论。

证明由已知条件知A╞Th(A)，从而Th(A)是和谐的理论。下证Th(A)的极大性。设β是L的

一个语句，且β∉Th(A)，即A不满足β,从而有A╞(┐β)，因此(┐β)∈Th(A)，所以Th(A)∪{β}├(┐β)且Th(A)∪{β}├β。由定理1知，Th(A)∪{β}不和谐，这样就得到Th(A)是极大和谐理论，证毕。

3 Lindenbaum定理的新证明

下面将用以上得到的结论巧妙地证明Lindenbaum定理。

定理2[1](Lindenbaum定理)L中每一个和谐的理论Σ都能扩张为一个极大和谐的理论。

证明设Σ为L中任一和谐的理论，则由引理1知，Σ有模型A，结合推论4得，Th(A) ={α：A╞α}为包含Σ的极大和谐理论，证毕。

4 应用

定理3[3]向量组α1,α2,…,αn中的任何一个线性无关组都可以扩充为一个极大线性无关组。

证明设向量组α1,α2,…,αn为L中的语句，设Σ为L中任意一个线性无关的语句所组成的理论。结合高等代数知识，得Σ的每一有限子集都有模型，从而由引理3知，Σ有模型，即A╞Σ。则Th(A) ={α：A╞α}为包含Σ的极大和谐理论，证毕。

[1]王世强.模型论基础[M].北京:科学出版社, 1987:6-17.

[2]沈复兴.模型论导引[M].北京: 北京师范大学出版社, 1995:6-18.

[3]何军华，李永彬.高等代数[M].北京:高等教育出版社, 2012:117-131.

[编辑] 洪云飞

O141.4

A

1673-1409(2013)22-0017-02

2013-05-12

安徽省高校自然科学研究重点项目(2005KJZD)。

万展翔(1988-)，男，硕士生，现主要从事数理逻辑及应用方面的研究工作。