变形双重介质分形油藏不稳定渗流数学模型有限元法求解研究
2013-11-06泸州医学院生物医学工程系四川泸州646000
张 勇 (泸州医学院生物医学工程系,四川 泸州 646000)
何国良 (电子科技大学数理学院,四川 成都 611731)
变形双重介质分形油藏不稳定渗流数学模型有限元法求解研究
张 勇 (泸州医学院生物医学工程系,四川 泸州 646000)
何国良 (电子科技大学数理学院,四川 成都 611731)
变形双重介质分形油藏的不稳定渗流数学模型,当边界条件为第一类边界条件时,用预估-校正法可以很好地解决;当边界条件含有第二类边界条件时,证明差分解的存在性和收敛性时却遇到巨大困难。为了较为简单地解决上述问题,采用有限元方法求其数值解,并证明了有限元离散解的存在性和收敛性,为其在石油工程中的应用提供理论依据。
不稳定渗流;收敛;有限元法;收敛性
在石油勘探和开采中,利用计算机技术进行油藏数值模拟是了解地下储油变化的一项简便方法。为此,研究者提出相关模型和算法。Warren-Root模型建立在均质油藏欧几里得几何基础上,不适用于具有压力敏感效应的非均质油藏[1]。文献[2]以Warren-Root模型为基础,引入分形参数df、θ和压缩系数αf、βf,考虑压力对具有分形特征的渗透率和孔隙度的影响,建立变形双重介质分形油藏不稳定渗流数学模型如下:
(1)
(2)
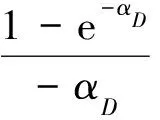
上述模型可用来刻画具有轴称特征的地下油藏,然而由于该模型的复杂性,如何高效求解成为一个亟待解决的问题。
1 含有第二类边界条件渗流数学模型的有限元离散
当边界条件为第一类边界条件(井底定压和有界定压外边界)时,用预估-校正法[2]可以很好地解决该类定解问题;当边界条件含有第二类边界条件(定产量和封闭外边界)时,对差分解的存在性以及收敛性的证明却十分困难。因此,为了较为简单地解决上述问题,可以采用有限元方法来求其数值解。
在不引起混淆的情况下,令t=τ,τ=Δt,则将式(2)代入式(1)并记为如下形式:

(3)
其中:
f1(u,η)=ωe(θ+2)u(1-αDη)γD-1f(u,η)=(β-1)
定解条件上述各条件令l=lnRe,记:
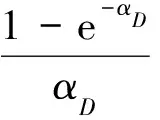
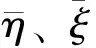
将式(3)按如下格式对时间进行离散化:

于是有:
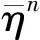
(4)
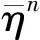
用单元线性插值的有限元方法求解式(10)和其定解条件。对于不同的边界条件选取不同类型的有限元空间sh,其都满足通常的逼近性质和逆性质[3]。


(5)
于是可得到方程组为:
CP=G
(6)


(7)

2 有限元离散的渗流数学模型的收敛性分析
为了证明该有限元算法的收敛性,可以在解存在、有界性的基础上利用经典的Gronwall不等式来进行分析。


为方便起见,记:
(8)
式(3)、式(2)所对应的弱解形式在各边界条件下为:
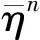
(9)
其中HΓ由式(8)来定义,且由式(3)有:

(10)
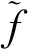



设Pi为原始地层压力,则PfD为一有界量,不妨设为PD0,则在有限区域Ω:Ω={0 |f1(u,ηn)-f1(u,ηn-1)|≤C2ωe(θ+2)l|ηn-ηn-1|C2=αD(1-γD)(1-αDη*)γD-2 于是由式(2)、式(3)、式(9)及边界条件,可得误差方程为: (11) 其中: Fn=( 取检验函数v=dtζn,则有: 有: 此外: 利用分部积分和分部求和有: 将式(11)两端同乘以2τ,并对n从2到M-1(m≤N)求和有: 则当h和τ充分小时,由离散的Gronwall不等式有[5]: 在式(11)中,取n=1,v=d1ζ1,有: 从而有: 由此该有限元离散解的的收敛性得到证明。 数学建模同数值模拟相结合是解决复杂问题的便捷而有效的分析工具。有限元方法是求偏微分方程中使用较为普遍的方法,其对边界条件恰如其分的处理是其他许多方法无可比拟的。当建立的变形双重介质分形油藏不稳定渗流数学模型的定解问题含有第二类边界条件时,由于相关方程是非线性的,为了克服有限差分法证明其离散解的存在性和收敛性时遇到的困难,利用有限元法解决该类定解问题。研究表明,利用有限元方法能够方便、简洁地证明有限元离散解的存在性和收敛性,从而为变形双重介质分形油藏不稳定渗流数学模型应用于石油工程提供理论参考。 [1]Warren J E,Root P J.The behavior of naturally fractured reservoirs[J].SPE13245,1963. [2]何国良,向开理.变形双重介质分形油藏渗流数学模型及压力动态特征[J].西南石油学院学报,2002,24(4):24-27. [3]Dendy J E.An analysis of some Galerkin schemes for the solution of nonlinear time-dependent problems[J].SIAM J Numer Anal,1975,12(4): 541-565. [4]Wheeler M F.A priori -error estimates for Galerkin approximations to parabolic differential equations[J].SIAM J Numer Anal,1973,10(4):723-759. [5]袁益让,王宏.非线性双曲型方程有限元方法的误差估计[J].系统科学和数学,1985,5(3):161-165. [编辑] 李启栋 O29 A 1673-1409(2013)22-0013-04 2013-05-14 张勇(1976-)男,硕士,讲师,现主要从事数据挖掘方面的教学与研究工作。
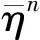
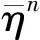
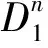
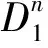
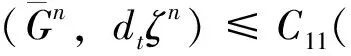
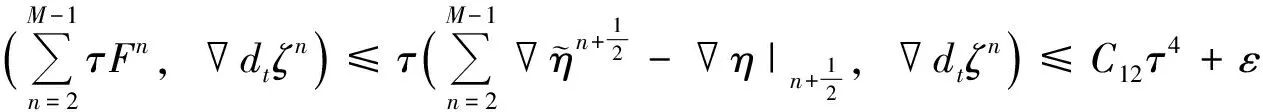

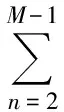



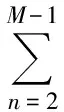




3 结语
