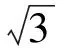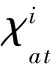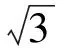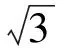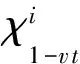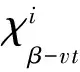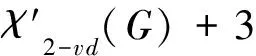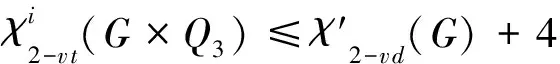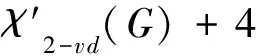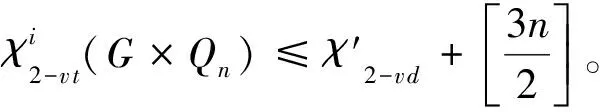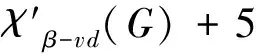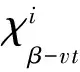D(β)-点可区别I-全染色的上界研究
2013-11-06刘利群长江大学信息与数学学院湖北荆州434023
刘利群 (长江大学信息与数学学院,湖北 荆州 434023)
陈祥恩 (西北师范大学数学与信息科学学院,甘肃 兰州 730079)
D(β)-点可区别I-全染色的上界研究
刘利群 (长江大学信息与数学学院,湖北 荆州 434023)
陈祥恩 (西北师范大学数学与信息科学学院,甘肃 兰州 730079)
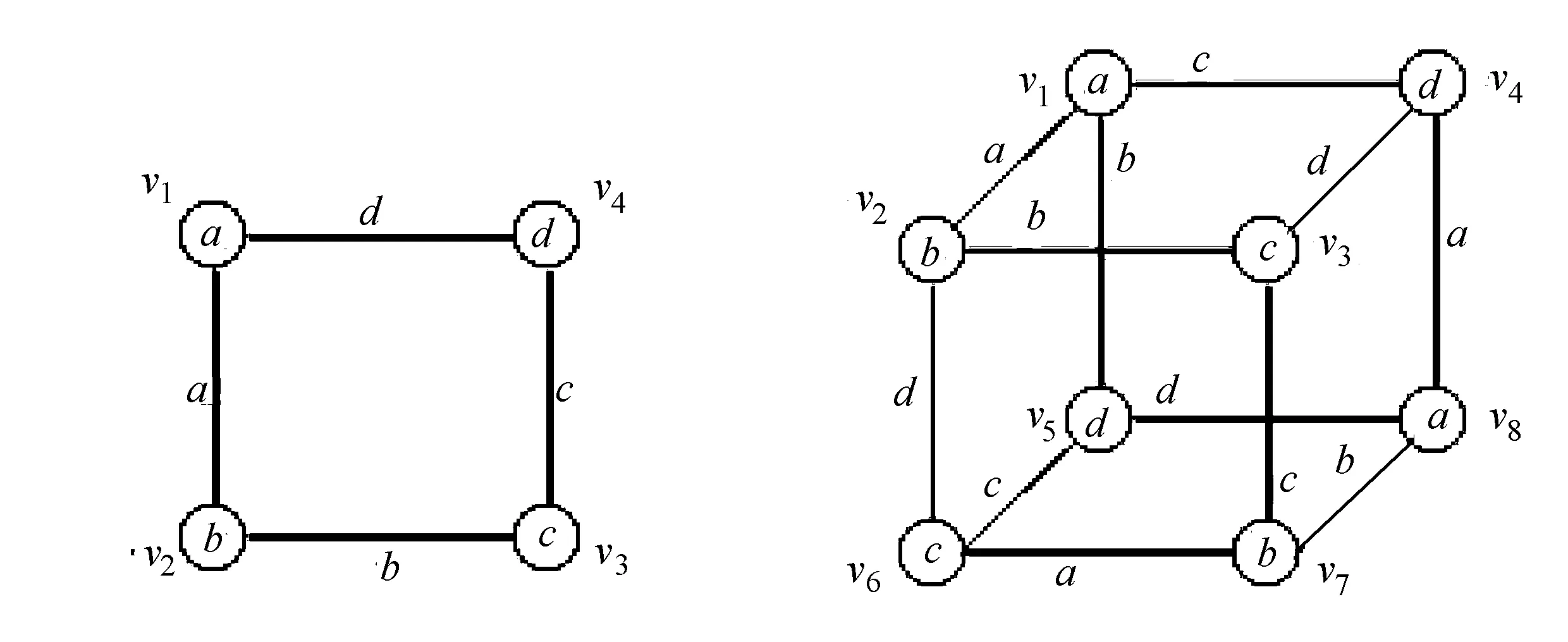
设G是简单图,若图G的全染色f满足:①∀uv,vw∈E(G),有f(uv)≠f(vw); ②∀uv∈E(G),u≠v,有f(u)≠f(v); ③∀u,v∈V(G),0 D(β)-点可区别I-全染色;D(β)-点可区别I-全色数;上界 图的染色问题是图论中具有重要实际意义和理论意义的研究课题之一。笔者考虑的图均为没有孤立边,最多有一个孤立点的有限无向单图。1997年,Burris A C和Schelp R H引入了图的点可区别的正常边染色(即强边染色)的概念[1], 此后,许多学者对图的染色的理论作了大量的研究。文献[1-4]研究了点可区别的正常边染色;文献[5]提出了邻点可区别正常边染色(即邻强边染色)的概念;文献[6-8]研究了D(β)-点可区别的正常边染色; 文献[9-10]研究了全染色。 定义1[3]G(V,E)是阶至少为3的连通图,α、β是正整数,f是从E(G)到{1,2,…,α)的一个映射。对∀e∈E(G),称f(e)为边e的颜色。对任意∀x∈V(G),令S(x)表示与x关联的边的颜色所构成的集合, 称为点x的色集合。若f是图G的正常边染色, 且当u、v∈V(G),0 定义2图G的正常点染色是对图G的每个顶点都指定一种颜色,使得没有2个相邻的顶点指定为相同的颜色。如果这些颜色选自于一个有k种颜色的集合而不管k种颜色是否都用到,这样的染色称为k-正常点染色。若f是G的一个使用了k种颜色的正常点染色,满足:当u、v∈V(G),0 定义3图G的全染色叫做图G的正常全染色,如果以下3个条件被满足,条件(v):相邻的3个顶点不能染相同的颜色;条件(e):相邻的2条边不能染相同的颜色;条件(i):任意的点和与之关联的边不能染相同的颜色。 如果图G的全染色只满足条件(e),这样的全染色称为图G的VI-全染色;如果图G的全染色满足条件(v)和条件(e),这样的全染色称为图G的I-全染色。 定义4若f是G的一个使用了k种颜色的全染色,满足:①对任意相邻的边e1、e2,有f(e1)≠f(e2); 证明假设图G(V,E)已给出,分以下4个步骤对图G进行全染色。 第1步 由Vizing定理,可先用Δ(G)+1种颜色对G进行正常边染色,再用Δ(G)+1种颜色对G进行正常点染色,这样就得到了G的全染色。 第2步 取一种新颜色a,对G的每个顶点随机独立的挑选它的一条关联边用新颜色a重染(这时,边e=uv被新颜色a重染的概率是1/(deg(u))+1/(deg(v)))。 第3步 在第2步完成后,另取一种新颜色b,再对G的每个顶点随机独立的挑选它的一条关联边用新颜色b重染。注意:新颜色b可能覆盖新颜色a。 第4步 在第3步完成后,另取一种新颜色c,再对G的每个顶点随机独立的挑选它的一条关联边用新颜色c重染。注意:新颜色c可能覆盖新颜色a、b。 下面证明以下2点成立的概率为正:①此全染色满足没有相邻2条边或相邻的2点着色相同;②此全染色是邻点可区别的即对任意相邻2点u、v(uv∈E(G)),有S(u)≠S(v)。 为此,定义如下坏事件:(Ⅰ)对每对相邻的边e、f∈E(G),令Ae,f表示e和f被染成同种颜色的事件;(Ⅱ)对每一条边e=uv∈E(G),令Bu,v表示u和v的关联边是正常着色且S(u)=S(v)的事件。下面证明上述坏事件都不发生的概率为正。 构造相关图D,其中D的顶点是以上2种类型的所有事件,设EX、EY是D的2个顶点(每个X、Y是一对相邻边,或者是和一条边相邻的所有边及其这条边本身。EX和EY是相邻的当且仅当X和Y至少包含一条公共边。由于EX的每个事件发生依赖于X的边,从而D是事件的相关图。首先,需要计算每个坏事件发生的概率,有以下2条成立:对类型(Ⅰ)的每个事件Ae,f,有Pr(Ae,f)≤3/δ2;对类型(Ⅱ)的每个事件Bu,v,有Pr(Bu,v)≤6/d3。 下面首先证明Pr(Ae,f)≤3/δ2。若事件Ae,f发生,则e,f被同种新颜色重染。设e的端点是w1、w2,f的端点是w2、w3,deg(wi)=di(i=1,2,3),若e、f都被颜色x(x=a,b,c)重染,有以下3种情况:(i)作为w1的关联边e被颜色x重染的概率为1/d1,同时作为w2的关联边f被颜色x重染的概率为1/d2,此时e、f同时被一种新颜色重染的概率为1/(d1d2);(ii)作为w1的关联边e被颜色x重染的概率为1/d1,同时作为w3的关联边f被颜色x重染的概率为1/d3,此时e、f同时被一种新颜色重染的概率为1/(d1d3);(iii)作为w2的关联边e被颜色x重染的概率为1/d2,同时作为w3的关联边f被颜色x重染的概率为1/d3,此时e、f同时被一种新颜色重染的概率为1/(d2d3)。故e、f同时被一种新颜色重染的概率不大于1/(d1d2)+1/(d1d3)+1/(d2d3)≤3/δ2。 其次证明Pr(Bu,v)≤6/d3。若事件Bu,v发生,则u和v有相同的色集合,且它们的色集合中都包含有a、b、c这3种颜色中至少一种。下面分以下几种情况进行讨论:(i)用Δ(G)+1种颜色对G进行全染色后,若u和v有相同的色集合,则Pr(Bu,v)≤3!/d3=6/d3;(ii)用Δ(G)+1种颜色对G进行全染色后,若u和v的色集合中有1种不同的颜色,则Pr(Bu,v)≤3×(3!)/d4≤6/d3;(iii)用Δ(G)+1种颜色对G进行全染色后,若u和v的色集合中有2种不同的颜色,则Pr(Bu,v)≤6×(3!)/d5≤6/d3;(iv)用Δ(G)+1种颜色对G进行全染色后,若u和v的色集合中有3种不同的颜色,则Pr(Bu,v)≤6×(3!)/d6≤6/d3;(v)用Δ(G)+1种颜色对G进行全染色后,若u和v的色集合中有大于3种不同的颜色,则Pr(Bu,v)=0。故对类型(II)的每个事件Bu,v,Pr(Bu,v)有≤6/d3。 然后计算相关事件数。对类型(I)的每个事件Ae,f,在D中Ae,f的相关点至多与类型(I)的4Δ个事件相关,至多与类型(II)的3Δ个事件相关;对类型(II)的每个事件Bu,v,在D中Bu,v的相关点至多与类型(I)的4Δ2个事件相关,至多与类型(II)的2Δ2个事件相关。 应用一般局部引理,可构造常数。令8/Δ2,1/(2Δ2)分别表示和(Ⅰ)、(Ⅱ)中的事件相应的常数,那么为了满足一般局部引理的条件,需要证明以下2个不等式成立: Pr(Ae,f)≤(8/Δ2)(1-8Δ2)4Δ(1-1/2Δ2)3Δ (1) 因为: Pr(Bu,v)≤(1/2Δ2)(1-8/Δ2)4Δ2(1-1/2Δ2)2Δ2 (2) 对所有实数x≥2,有(1-1/x)x≥1/4,所以当Δ≥67时有: (8/Δ2)(1-8/Δ2)4Δ(1-1/2Δ2)3Δ≥(8/Δ2)(1/4)32/Δ+3/2Δ=(8/Δ2)(1/2)67/Δ>4/Δ2 (1/2Δ2)(1-8/Δ2)4Δ2(1-1/2Δ2)2Δ2≥(1/2Δ2)(1/4)32+1=1/(267Δ2) 故定理1得证。 定理2设G1、G2是连通图,则有: 定理3设G(V,E)是连通图, 则有: 证明设vw∈E(G),若将v、w分别用Q2的拷贝代替,其顶点分别为vi、wi(1≤i≤4),其中vi与wi相邻。于是得到积图G×Q2,其中Gvw(将v、w分别用Q2的拷贝代替后得到的图)与Q3同构。设η是G的一个D(2)-点可区别正常边染色,所用颜色为{1,2,…,m};θ是Q2的一个D(2)-点可区别I-全染色,所用颜色为{a,b,c,d},其中f(v1)=f(v1v2)=a,f(v2)=f(v2v3)=b,f(v3)=f(v3v4)=c,f(v4)=f(v1v4)=d(如图1所示)。 分别用η染色法及θ染色法对G×Q2进行着色,设在η染色法下G中一条边vw着颜色t∈[1,m],v,w的色集合分别为X,Y(显然X≠Y)。将G中所有着t色的边按下述方法改变颜色:v1w1改成颜色b,v2w2改成颜色c,v3w3改成颜色d,v4w4改成颜色a。则有: S(v1)=(X|t)∪{a,b,d}S(v2)=(X|t)∪{a,b,c}S(v3)=(X|t)∪{b,c,d} S(v4)=(X|t)∪{a,c,d}S(w1)=(Y|t)∪{a,b,d}S(w2)=(Y|t)∪{a,b,c} S(w3)=(Y|t)∪{b,c,d}S(w4)=(Y|t)∪{a,c,d} 图1 图θ2 图2 图θ3 定理4设G(V,E)是连通图, 则有: 证明设vw∈E(G),若将v,w分别用Q3的拷贝代替,其顶点分别为vi、wi(1≤i≤8),其中vi与wi相邻。于是得到积图G×Q3。设η是G的一个D(2)-点可区别正常边染色,所用颜色为{1,2,…,m};θ是Q2的一个D(2)-点可区别I-全染色,所用颜色为{a,b,c,d},其中: f(v1)=f(v8)=f(v1v2)=f(v6v7)=f(v4v8)=a f(v2)=f(v7)=f(v1v5)=f(v2v3)=f(v7v8)=b f(v3)=f(v6)=f(v1v4)=f(v3v7)=f(v5v6)=c f(v4)=f(v5)=f(v3v4)=f(v2v6)=f(v5v8)=d(如图2所示)。 分别用η染色法及θ染色法对G×Q3进行着色, 设v、w是G的2个顶点,且v、w的距离不超过2,v、w在η染色法下的色集合分别为X,Y(显然XY)。则有: S(v1)=S(v7)=X∪{a,b,c}S(v2)=S(v8)=X∪{a,b,d} S(v3)=S(v5)=X∪{b,c,d}S(v4)=S(v6)=X∪{a,c,d} S(w1)=S(w7)=Y∪{a,b,c}S(w2)=S(w8)=Y∪{a,b,d} S(w3)=S(w5)=Y∪{b,c,d}S(w4)=S(w6)=Y∪{a,c,d} 定理5设G(V,E)是连通图, 则有: 证明当n=2r(r为正整数),由定理3,有: 当n=2r+1(r为正整数),由定理3及定理4,有: 类似结论可推广到D(β)-点可区别I-全染色: 定理6设G(V,E)是连通图, 则有: 定理7设G(V,E)是连通图, 则有: 证明设vw∈E(G),若将v、w分别用Q3的拷贝代替,其顶点分别为vi、wi(1≤i≤8),其中vi与wi相邻。于是得到积图G×Q3。设η是G的一个D(β)-点可区别正常边染色,所用颜色为{1,2,…,m};θ是Q2的一个6-D(β)-点可区别I-全染色,所用颜色为{a,b,c,d,e,h},其中: f(v1)=f(v7)=f(v1v2)=f(v6v7)=af(v2)=f(v8)=f(v2v3)=f(v7v8)=b f(v3)=f(v3v4)=f(v5v8)=cf(v4)=f(v1v4)=f(v5v6)=d f(v5)=f(v1v5)=(v3v7)=ef(v6)=f(v2v6)=f(v4v8)=h 定理8设G(V,E)是连通图, 则有: 证明当n=2r(r为正整数),由定理3,有: 当n=2r+1(r为正整数),由定理3及定理4,有: 因此有: [1]Burris A C, Schelp R H.Vertex-distinguishing proper edge-colorings[J].J of Graph Theory,1977,26:73-82. [2] Bazgan C, Harkat-Benhamdine A,Li Hao and Wozniak M. On the vertex-distinguishing proper edge-colorings of graphs[J]. Combin Theory B, 1999, 75: 288-301. [3] Balister P N, Bollobás B and Schelp R H. vertex-distinguishing colorings of graphs with Δ(G)=2[J]. Discrete Math, 2002, 252(1-3): 17-29. [4] Balister P N, Riordan O M and Schelp R H. Vertex-distinguishing edge colorings of graphs[J]. Graph Theory, 2003, 42: 95-109. [5] Zhang Zhongfu,Liu Linzhong,Wang Jianfang. Adjacent Strong Edge Coloring of Graphs[J]. Applied Mathematics Letters,2002, 15: 623-626. [6]张忠辅, 李敬文, 陈祥恩,等.图的距离不大β的任意两点可区别的边染色[J].数学学报, 2006, 49(3): 703-708. [7]Akbari S,Bidkhori H,and Nosrati N.r-strong edge colorings of graphs [J]. Discrete Mathematics, 2006, 306:3005-3010. [8]刘利群,陈祥恩.路和圈上的锥的D(2)-点可区别正常边染色[J].山东大学学报, 2008, 43(2): 87-97. [9]ZHANG Zhongfu,QIU Pengxiang,XU Baogen,et al.Vertex-distinguishing total colorings of graphs[J]. Ars Combinatoria,2008,87:33-45. [10]CHEN Xiang-en, GAO Yu-ping, YANG Sui-yi. Various General Total colorings of Graphs[J]. Journal of Jishou University(Natural Science Edition), 2011, 32(1):1-3. [11]Balister P N,Györi E,Lehel J,et al. Adjacent Vertex Distinguishing Edge Colorings[J]. SIAM Journal on Discrete Mathematics, 2007, 21(1): 237-250. [12]Hatami H. Δ+300 is a bound on the adjacent vertex distinguishing edge chromatic number[J]. Combin Theory, Ser B, 2005, 95:246-256. [13]Alon N, Spencer J. The Probabilistic Method[M]. New York:John Wiley & Sons Inc,1992. [14]Molloy M, Reed B. Graph Colouring and the Probabilistic Method[M]. New York:Springer, 2002. [编辑] 洪云飞 O157.5 A 1673-1409(2013)22-0001-05 2013-05-20 国家自然科学基金资助项目(61163037;61163054);西北师范大学“知识与科技创新工程”项目(nwnu-kjcxgc-03-61)。 刘利群(1977-),女,硕士,讲师,现主要从事图论及其应用方面的教学与研究工作。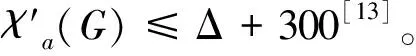
1 基本概念
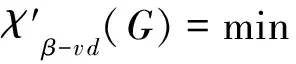
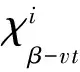
2 主要结果与证明