基于航迹片段树的快速四维航迹规划方法
2013-11-05张险峰
张险峰
(北京航空航天大学 宇航学院,北京100191)
周其忠 王长青
(北京机电工程研究所,北京100074)
随着信息化的发展,时间因素在现代战争飞行器使用中的影响越来越突出.这不仅要求能快速完成飞行器的航迹规划,还希望在无人飞行器作战使用时,能在比较充裕的发射时间段内发射,且还能按指定时间到达目标.在无人飞行器本身具备一定时间控制能力情况下,时间作为一个不可忽视的因素,开始受到人们的关注和重视.2008年,赵明元[1]等基于启发式A*算法提出了一种四维实时航迹规划方法,通过在飞行过程中实时调整推力以解决准时到达目标的问题.2009年,严江江[2]等提出了一种基于进化算法的多飞行器四维航迹规划方法,通过在三维航迹规划的基础上加入时间代价约束,完成多个无人飞行器能够同时到达并避免飞行过程中的相互碰撞.2011年,傅阳光[3]等也提出了一种基于进化算法的航迹规划方法,并对发射时间误差、飞行器速度调整能力及飞行速度误差3个因素对飞行器到达目标点时间误差的影响展开了研究.
尽管这些文献都考虑了时间维,但文献[1]主要研究了飞行器沿指定航迹飞行过程中的在线四维航迹调整,未考虑组合导航对地形、景象的要求,且不适于平时规划,文献[2]采用整个航程内的平均速度来计算飞行时间,同时没有考虑起飞时间误差以及飞行速度本身因控制以及外部环境产生的时间误差,文献[3]虽然考虑因素全面,但存在规划结果不确定,且时间长的不足.这均与无人飞行器快速作战使用需求有一定的差距.
本文首次提出航迹片段树的概念,以预先指定的起飞区域/点(实际情况下,这些信息是明确的)为根节点,利用改进的稀疏A*算法,在考虑飞行器组合导航、时间调整以及各种机动性能约束的前提下,生成覆盖整个规划区范围的立体空间航迹片段树.对于任意指定的目标点,均可以通过在该树中寻找最优叶节点,并通过回溯以及速度优化设置,快速完成四维航迹规划.
1 问题描述及假设
为达到预期目的,往往对飞行器到达指定地点的时间有严格要求.一般情况下,航迹规划给出的航迹只给出了理论飞行时间,而在实际使用时,无人飞行器的实际起飞时间将与预期要求有一定的误差,并且无人飞行器在飞行过程中因风向、风力等气象因素,以及飞行器本身的控制误差影响,使得实际到达指定地点的时间有较大误差.
为解决该问题,现代的无人飞行器具备了速度自主调整能力:即在飞行过程中,能根据当前飞行时间以及预期时间的差值,在一定的速度范围内进行速度的自主调整,使得尽可能消除当前飞行时间误差,对于消除之后剩余的时间误差,将由下一个航段消除.依次类推,直至按指定时间到达指定地点.
为便于后续讨论方便,本文作如下假设:
1)起飞区域预先指定;
2)起飞时间偏差dT:是指起飞时间与预期起飞时间的偏差,可提前也可推迟,一般为数分钟;
3)飞行速度误差dV:无人飞行器飞行过程中因风等气象环境以及飞行器本身控制等因素所造成的综合速度误差;
4)速度调整能力kV:无人飞行器在飞行过程中速度自主调整能力范围,本文假设只能在平直飞行状态下才能进行速度自主调整,且可在整个速度包线范围[Vmin,Vmax]内进行调整;
5)速度调整策略:在飞行过程中,无人飞行器在当前航段飞行过程中尽可能多的消除进入该段之前的累计时间误差.
无人飞行器的其他相关约束如下:
1)飞行高度约束.在规划过程中需考虑无人飞行器的最大飞行高度限制、最小安全飞行高度以及在空中管制区域的飞行高度限制;
2)飞行速度约束.无人飞行器的飞行速度可在速度包线范围内进行设置;
3)爬升/下滑速度约束.由于无人飞行器本身性能限制,爬升/下滑的速度是有限的,一般是每秒数十米;
4)转弯半径/角度约束.无人飞行器有最小转弯半径的限制,并且该最小转弯半径随飞行速度的提高而加大;
5)精确导航要求.从一个航迹片段进入下一个航迹片段时,要保证惯导误差散布要求;
6)禁飞区限制.航迹片段不能通过禁飞区;
7)航程约束.无人飞行器具有最大飞行航程限制.
2 航迹片段树表达及航迹回溯
对于长航时飞行器来说,在不使用GPS或没有GPS信号的情况下,每飞行一段距离后则需要寻找一个地面信标台或典型地物标识进行导航修正,以避免因导航误差过大而无法执行后续任务.由于最大导航距离不仅依赖于刚刚经过的信标修正或地物修正的惯导导航精度,而且与下一次修正时刻对导航误差的容忍程度也密切相关.这种紧密的航迹前后依赖关系造成无法事先确定出最大导航距离参数.如果将该问题留给航迹搜索算法,当搜索到最大导航距离之后仍未找到合适的导航修正手段,搜索算法就必须回退.为避免上述问题,提高搜索效率,提出了基于导航修正点航迹片段树的搜索算法.
如图1所示为本文所定义的航迹片段树示意图.图中的每个片段上均有一个信标台或地物修正点(矩形框所示).在本研究中,航迹片段树具有如下特点:①相邻两个片段之间最多有一个高度变化点或一个转弯点;②相邻两个导航修正点之间的飞行时间满足最大导航误差散布的要求;③相邻两个航迹片段之间满足最短距离限制;④每个节点均有唯一标识,并且包含指向其父节点的标识.
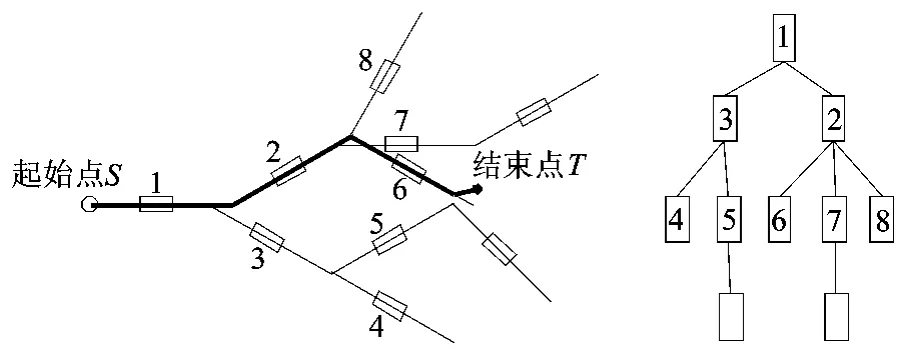
图1 航迹片段树示意图
通过该航迹片段树,可以将整个规划空间进一步表达为可行航迹空间,航迹规划时即可直接从该航迹片段树中进行搜索,避免了在实际规划空间中的航迹复杂搜索.该航迹片段树中任意节点到其所扩展叶节点之间代表着是一条可行航迹,因此在指定结束点之后,可根据结束点进入约束寻找最优叶节点,然后通过其父节点标识回溯,直至回溯到根节点,完成航迹的快速规划.如图1所示,从起始点S到结束点T之间的航迹就可以通过回溯产生{T,6,2,1,S}.
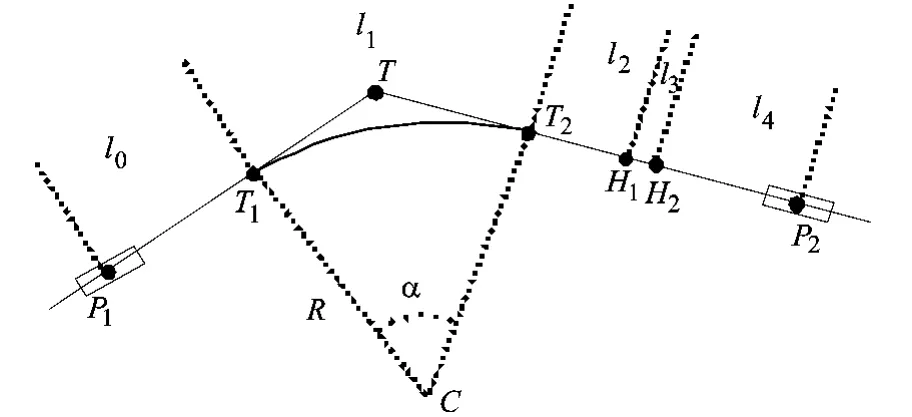
图2 航迹片段示意图
3 基于稀疏A*的航迹片段树生成
传统的基于概略图的方法中,Voronoi图[4]以及随机路线图[5]并不适合对三维复杂环境进行建模.另外,对于无人飞行器来说,其起飞区域相对固定,因此可以考虑以此区域附近一个点作为数的根节点,生成航迹树.本文采取基于约束的稀疏A*[6]算法,并进行适应性改进,用于航迹片段树的构建,以满足四维航迹快速规划的需要.
3.1 扩展区域计算改进
稀疏A*的扩展区域为一扇形区域,主要与转弯能力以及组合导航进区要求相关.角度范围与转弯角度范围限制一致,半径方向有最大长度和最小长度限制.在一般稀疏A*算法中,半径方向最短长度为前后两个导航修正点工作距离的半长度之和,最大长度为以当前飞行速度能满足进入下一个导航修正点惯导误差散布要求的距离.在这种扩展区域中所搜索的航迹,其可供飞行器进行速度调整的范围可能受到限制.为解决该问题,本文对最大长度的计算方法进行了改进:用可用速度包线的下限进行最大长度的计算.通过这种改进,使得所规划航迹的速度可在整个速度包线范围内进行设置,且满足进入下一个导航修正点的惯导误差散布要求.
3.2 代价函数改进
在常规稀疏A*算法中,代价函数由当前点代价和从当前点到目标的预估代价两项组成.在航迹片段树构建过程中,并没有指定目标用以引导算法的搜索,因此在航迹扩展过程中,只考虑当前点的航迹代价,即主要考虑飞行时间误差消除能力以及航程限制.
如图2所示航迹片段P1P2中(P1为当前扩展点,P2为扩展后的点),P2点的代价C2为
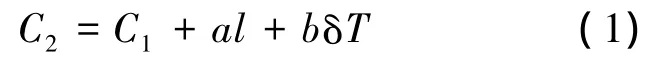
其中,l为该段扩展航迹片段的长度;δT为该航迹片段的最大最小飞行时间差;a和b则为相应的权系数.
航迹片段P1P2的最大、最小飞行时间按如下式子计算:
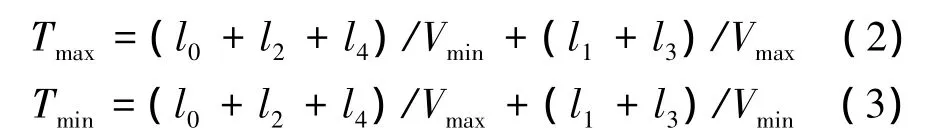
3.3 算法流程
1)初始化SAS算法运行环境.将open,closed表置为空;
2)将起飞区域赋值给节点cur,并把它放入closed表中;
3)根据当前节点cur的位置按起飞区域可用航向范围及航线约束条件确定下一个导航修正点的搜索方向和可行搜索空间(待扩展区),计算搜索空间的位置参数;
4)离散待扩展区.以导航修正点间最短距离和最长距离为半径的圆弧将待扩展区从距离上划分为M区域.然后每次旋转θ角度来划分这M个区域;
5)子区域中搜索导航修正点.
a)角度方向循环;
b)由远及近以离散后的子区域为单元,以单元中心方向开始往两侧搜索,检测子区域中是否存在可用的导航修正点;
c)若未搜索到导航修正点,转b);
d)若搜索到导航修正点,计算当前节点cur到该修正点之间的三维航线:①若该航线满足约束,则计算该片段的各种参数,并放入open表,并转a);②否则转b);
6)open表为空,则转8);否则从open表中取出第1项(代价最优),称为节点cur,并把它放入closed表中;
7)根据当前节点cur的位置及方向按转弯角度限制及航线约束条件确定下一个导航修正点的搜索方向和可行搜索空间(待扩展区),计算搜索空间的位置参数;转4);
8)保存closed表数据,构建航迹片段树.
4 基于航迹片段树的四维航迹规划
在给定起始点和指定任务结束点后,航迹规划过程可分为任务结束点到临近叶节点的搜索、航迹树回溯、速度优化设置3个环节.
根据任务结束点位置以及导航修正点间最大导航距离要求,从航迹片段树中搜索附近的节点.然后根据起飞时间误差从中选择满足要求的最优节点,并以此节点进行航迹回溯,生成一条完整的航迹.
在航迹搜索完成之后,需对每个航迹片段的速度进行设置.假设第i个航迹段的规划飞行速度为Vi,需要消除的时间误差为Ei(包含第i-1段消除之后的时间误差残余以及第i-1段本身因各种因素导致的飞行时间误差,其中在起始点的时间误差为dT).如图2所示,根据规划的速度,飞行时间为
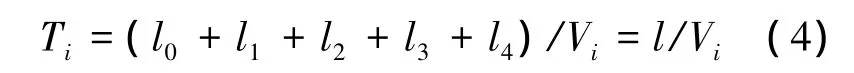
由于所生成的航迹片段满足整个速度包络内的速度使用要求,因此Vi可按误差最大消除考虑,有
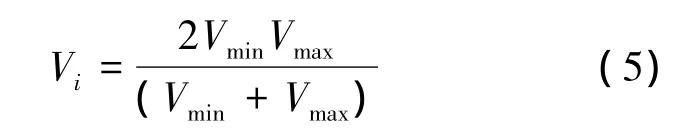
无人飞行器完成第i个航迹片段飞行后的时间误差残余为
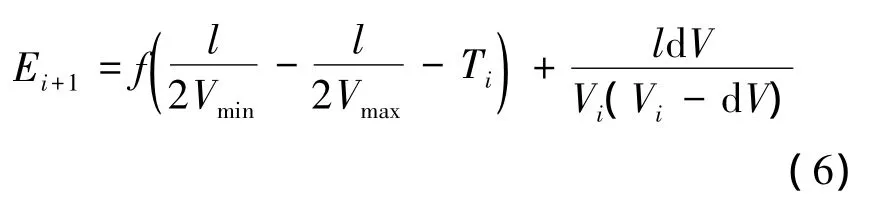
其中

5 仿真试验
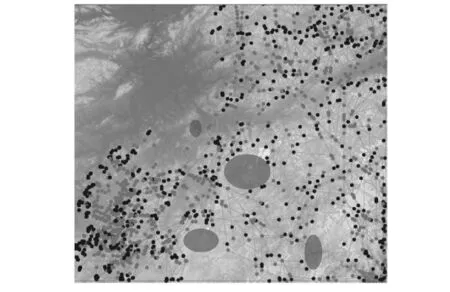
图3 规划区范围及航迹片段树示意图
如图3所示,本文给出了一个4.5°×4°的规划范围,空间粒度为1″.图中底图为该范围的高度灰度图,颜色越浅则代表海拔高度越高,其中椭圆区域表示各种人文、气象、拦截禁飞区.该图中给出了航迹片段树的示意,“黑点”表示该片段上各种属性的导航修正点,“灰点”表示转弯控制点,航迹片段为两个导航修正点之间的折线连线(在特殊情况下也有直线连接).
假设导航修正点之间的最大飞行时间间隔是300 s,无人飞行器飞行速度范围[200 m/s,300 m/s],最小转弯半径7.5 km,最大转弯角度±45°,爬升/下滑速度为30 m/s,最大航程1 000 km,飞行速度控制误差为±2 m/s.
图4 所示以(118.5°,23.5°)为起点,按速度包线中最慢速度产生的航迹片段树结果(航迹片段树节点总数为10 733,导航修正点之间最大距离60 km,最小距离30 km),以及任务结束点1(115.1,21.5)、任务结束点 2(116.25°,21.1°)以及任务结束点3(119.25°,21.75°)在不同起飞时间误差情况下的航迹示意图.其中“小旗”表示起飞位置,“三角”表示任务结束点.

图4 3个不同任务结束点的航迹规划结果示意图
在主频为2.83 GHz的计算机上,从航迹片段树(生成航迹片段树的时间为73min)中搜索航迹并完成速度优化设置的时间均为0.2~0.5 s,这表明本算法可以近实时完成航迹搜索.上述5条航迹的结果对比详见表1.
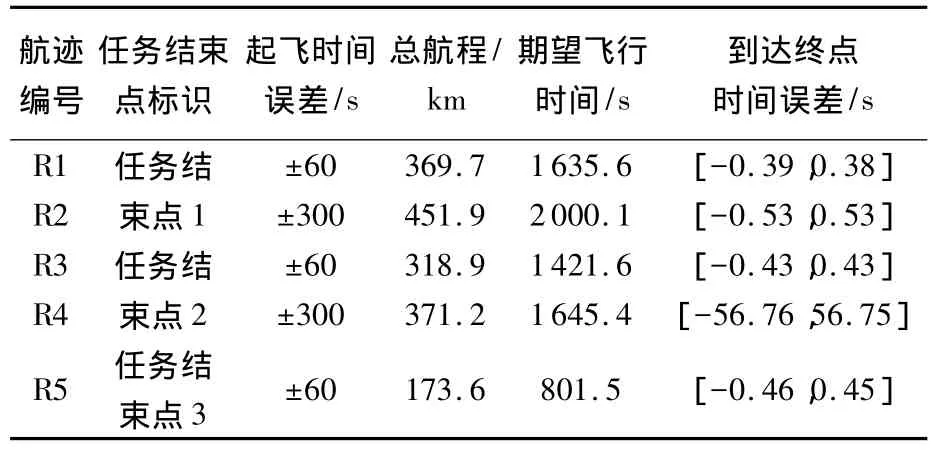
表1 航迹结果对比
从表1可以看出:①在无人飞行器飞行速度范围限定情况下,时间误差修正能力与航迹总长度有关,即航迹越长越可能消除时间误差;②由于飞行控制误差以及其他干扰情况的存在,使得无人飞行器到达指定地点的时间为一个范围,且最小为从最后一个导航修正点到指定地点之间因控制/气象因素造成的时间误差.
6 结束语
为消除起飞时间误差以及飞行过程中各种干扰对无人飞行器到达指定地点时间的影响,本文提出了一种基于航迹片段树的快速四维航迹规划方法.该方法通过对稀疏A*算法的扩展区域计算以及代价函数的设置进行了适应性改进,确保产生的航迹片段自然满足飞行器的各项约束,并将航迹搜索空间转换为航迹片段树;同时提出了航迹回溯以及最优速度设置方法,满足了能消除飞行器时间误差的四维航迹快速规划需求.试验结果表明,本文提出的方法可以近实时完成四维航迹规划,所规划的航迹能满足按时到达指定地点的要求.
References)
[1]赵明元,周军.基于A*算法的四维实时航迹规划算法[J].火力与指挥控制,2008,33(8):98-111 Zhao Mingyuan,Zhou Jun.Algorithm of 4D real-time path planning based on A*algorithm [J].Fire Control and Command Control,2008,33(8):98-111(in Chinese)
[2]严江江,丁明跃,周成平.基于进化算法的多飞行器四维航迹规划方法[J].系统仿真学报,2009,21(4):1125-1129 Yan Jiangjiang,Ding Mingyue,Zhou Chengping.4D route planning for multi-UAV based on evolutionary algorithm [J].Joural of System Simulation,2009,21(4):1125-1129(in Chinese)
[3]傅阳光,周成平,王长青,等.考虑时间约束的无人飞行器航迹规划[J].宇航学报,2011,32(4):749-755 Fu Yangguang,Zhou Chengping,Wang Changing,et al.Path planning for UAV considering time constrait[J].Journal of Astronautics,2011,32(4):749-755(in Chinese)
[4] Bhattacharya P,Gavrilova M L.Roadmap-based path planning using the Voronoi diagram for a clearance-based shortest path[J].IEEE Robotics & Automation Magazine,2008,15(2):58-66
[5] Baumann M A,Dupuis D C,Leonard S,et al.Occlusion-free path planning with a probabilistic roadmap[C]//2008 IEEE/RSJ International Conference on Intelligent Robots and Systems,IROS Nice.France:Inst.of Elec and Elec Eng Computer Society,2008:2151-2156
[6]周其忠.复杂环境下多UCAV协同规划技术研究[D].武汉:武汉大学测绘学院,2010 Zhou Qizhong.Research on cooperative planning for multiple UCAVs in complicated environments[D].Wuhan:School of Geodesy and Geomatics,Wuhan University,2010(in Chinese)
