FDTD方法的改进及在超声波声场计算中的应用

徐 娜 李 洋 周正干

(北京航空航天大学 机械工程及自动化学院，北京100191)

于 光

(上海飞机制造有限公司 航空制造技术研究所，上海200436)

超声检测具有检测范围广、检测深度大、使用方便、速度快等特点，是国内外应用最广泛的无损检测技术之一.然而，由于声学的实际应用问题很少能有严密的理论解，因此，从超声传播理论入手，研究声波在介质中的传播及与缺陷的相互作用规律，建立超声检测系统模型，是超声检测的重要发展方向之一［1］.

时域有限差分法 (FDTD，Finite-Difference Time Domain)最初是一种电磁场数值计算的方法，目前被广泛用于模拟弹性波在复杂介质中的传播.其差分格式中包含有介质的参量，只需赋予各网格相应的参量，即可模拟各种复杂的结构.另外，该方法采用步进法进行计算，易于实现各种复杂时域宽带信号的模拟，可方便获得超声波声场在空间分布的可视化及某一空间点的时域信号波形［2］.采用FDTD方法对超声波声场进行数值计算，目前已有许多报道，如文献［2］应用FDTD方法对弹性固体中的声场方程进行了二维声场特性研究，文献［3］采用FDTD方法对相控阵超声检测中声场与缺陷的相互作用进行了数值仿真.

通常情况下，为了保证算法稳定性，FDTD方法计算参数的选取需要满足两个限制条件，即仿真空间间隔远小于超声波在被检试件中传播的波长，仿真时间间隔应根据Courant限制条件来选取［4-5］.但是，在实际声场计算中发现，当相邻两种介质的声学参数相差较大时，采用Courant限制条件来选取计算参数无法保证算法的稳定性［5］，大大降低了FDTD方法在超声波声场计算中的实用性.并且，在实际工程检测中，常会遇到被检对象中相邻两种介质的声阻抗相差很大的情况，或者耦合介质与被检工件的声阻抗相差很大的情况(例如采用空气作为耦合介质).因此，如何有效解决FDTD方法数值稳定性的问题，显得尤为重要.

为了解决FDTD方法数值稳定性的问题，很多学者都做过探讨研究，提出了一些改进方法［6-8］，但大多应用在电磁场数值计算中，很少研究其在超声波声场计算中的应用.因此，本文研究FDTD方法在超声波声场计算中的应用，通过对FDTD方法的改进拟解决其数值稳定性的问题，从而改善其在超声波声场计算中的实用性.

1 FDTD方法及其改进

1.1 常规二维弹性波动方程的差分计算

声场变量常用质点速度ν和应力σ表示，二维x-z平面弹性波动方程［9］为

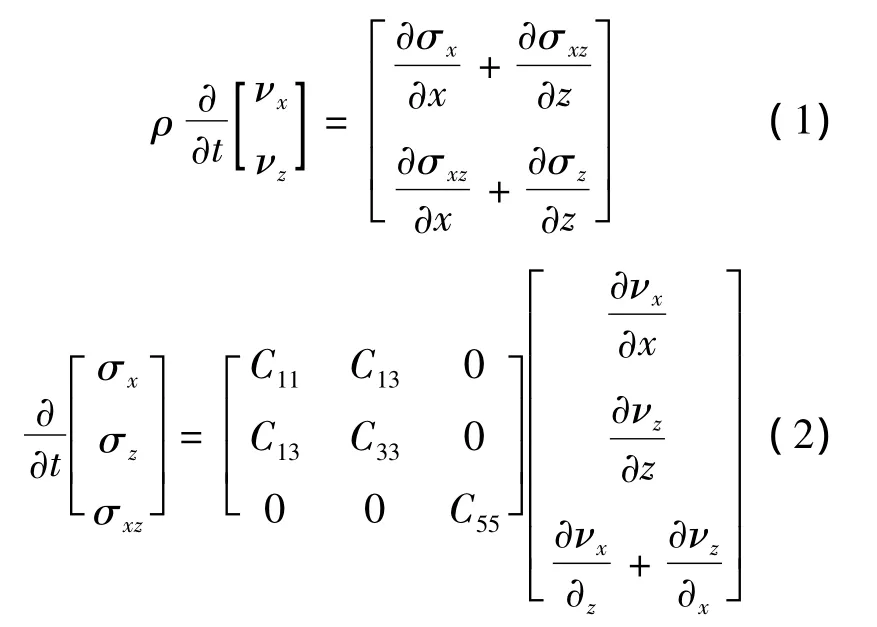
式中，ρ为质点密度;νx和νz分别为x和z方向的质点速度;σx和σz分别为空间各点x和z方向的正应力;σxz为切应力.式(2)中的系数矩阵由材料的弹性模量及泊松比确定，对于各向同性介质，该系数矩阵满足:

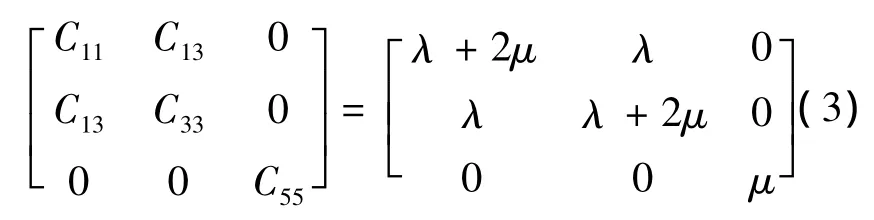
式中，λ和μ是拉梅常数，也称为切变弹性系数.

取Δx和Δz分别为x和z方向的空间采样间隔，T为时间采样间隔，使用常规的有限差分法推出的差分计算公式，如式(4)～式(8):

实际计算过程中，按照如下步骤进行计算:

1)利用式(4)和式(5)计算(n+1/2)T时刻空间处质点速度νx和νz的值;

2)利用式(6)～式(8)计算(n+1)T时刻空间各处应力σx，σz及切应力σxz的值;

3)回到步骤1)，将计算得出的(n+1/2)T及(n+1)T时刻的值分别作为(n-1/2)T及nT时刻的值，计算得出下一时刻的 νx，νz，σx，σz及σxz的值，不断重复迭代从而实现数值模拟.

1.2 FDTD方法的改进

由于差分是利用空间某点及其周围点对该点的描述，因此对微分方程进行差分离散后不可避免地会引入其他空间点的信息，而当引入的其他空间点的属性与原来该点的属性相差较大时，差分方程将无法正确表述原微分方程.因此，当相邻两种介质的声学参数相差较大时，在两种介质的分界面上经过差分计算的方程组就无法正确表达原微分方程，从而引起差分算法的不稳定.

针对该问题，提出将界面两边介质的声学参数在界面处进行平均处理，从而缓解两者介质声学参数在界面处的突变问题，减小数值计算的误差，提高算法的稳定性.对FDTD方法进行改进，提出对波动方程式(1)和式(2)先进行积分处理，然后再进行差分离散处理，使由于引入其他空间点的信息而产生的误差在很大程度上得到削弱.

以图1为例介绍改进的FDTD方法.图1是波动方程差分计算的离散网格示意图，其中质点速度νx，νz以及切应力σxz处于介质1和介质2的界面上.首先对式(1)的方程1进行积分处理:

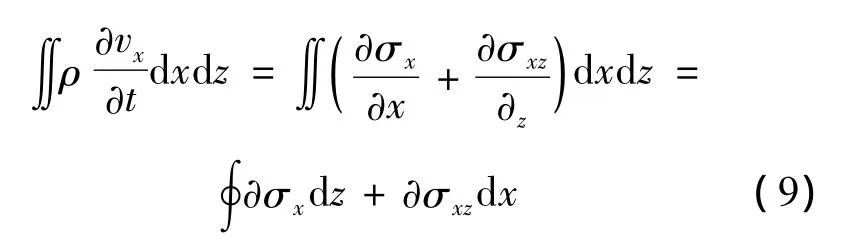
其积分范围为

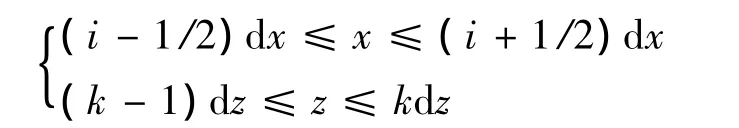
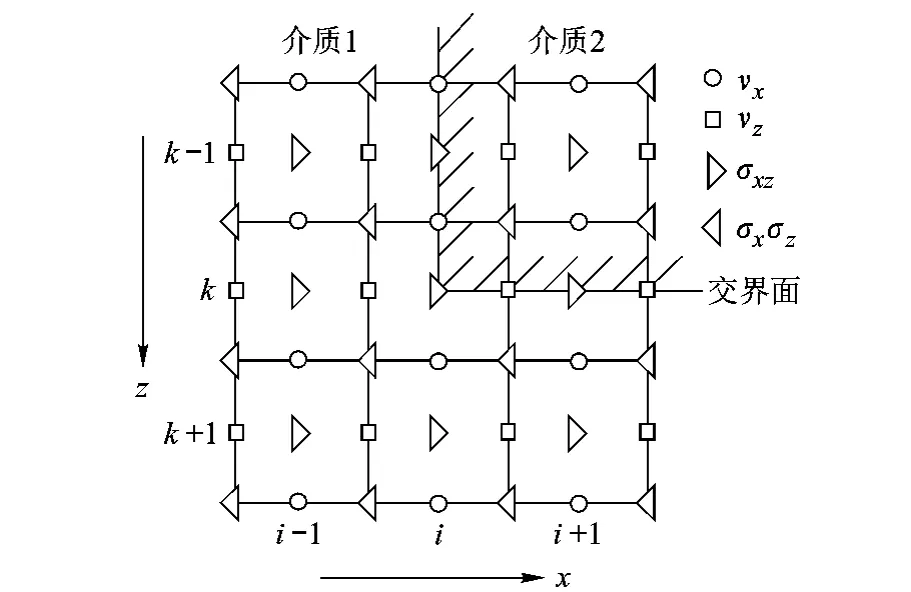
图1 差分算法的离散网格示意图

根据积分中值定理，对式(9)进行离散近似，可得

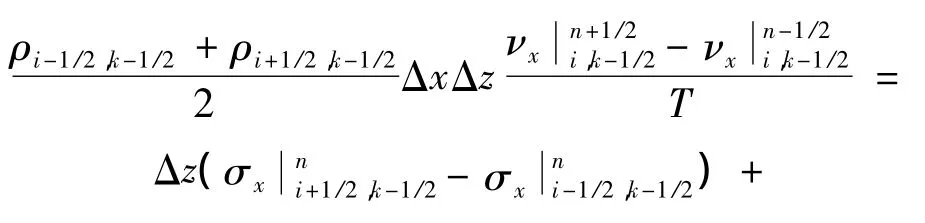
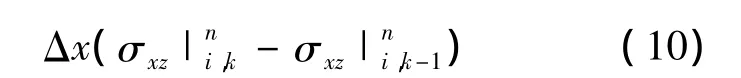
采用相同的积分计算方法对式(1)的方程2以及式(2)的3个方程进行计算，可得式(11)～式(14):

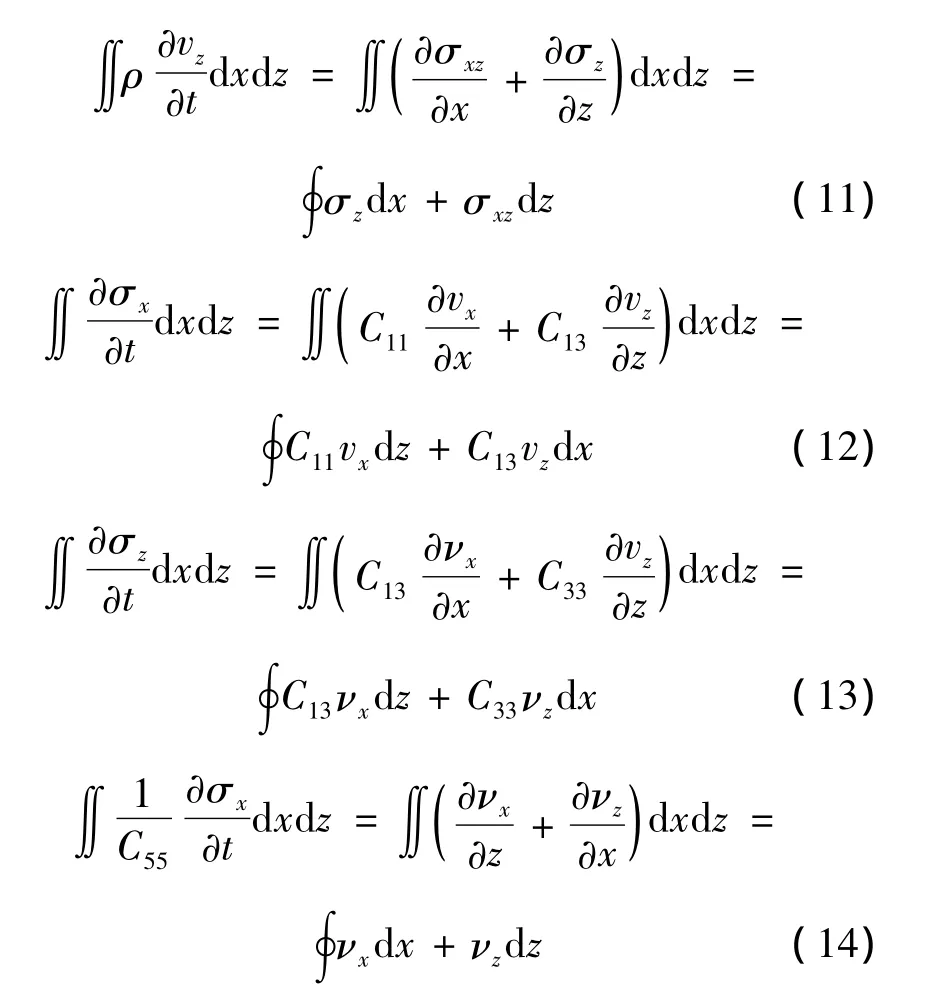
式(11)的积分范围为

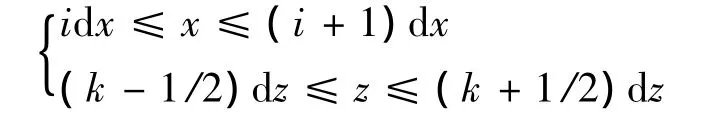
式(12)、式(13)积分范围为

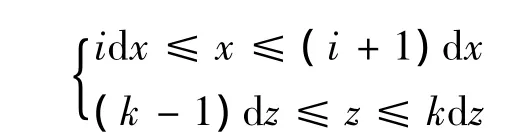
式(14)的积分范围为

通过计算，使用改进的有限差分法推出的差分计算表达式如式(15)～式(19)所示.可看出式(17)和式(18)与利用常规FDTD方法获得的差分表达式(式(6)、式(7))是一致的，这是因为正应力σx和σz没有位于两种介质的分界面上.但σxz位于其上，所以如式(19)所示，对式(2)中方程3的系数项C55进行了简单平均处理.

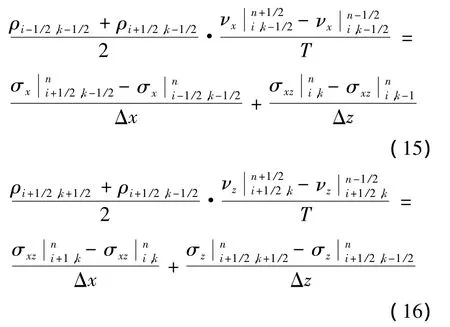
通过该方法得到的差分表达式实质上是对常规差分格式中相邻两种介质分界面上的系数项进行了简单平均处理，从而解决相邻两种介质声学参数相差太大而造成的差分计算不稳定的问题.

2 FDTD方法改进前后的对比

建立图2所示的仿真模型.试样参数:空气层，厚度7.5 mm，密度 ρ=1.169 1 kg/m3，纵波声速 νl=340m/s，声阻抗 Z0=3.97 ×102Pa·s/m3;金属层，厚度12.5 mm，密度ρ=7700 kg/m3，横波声速 νt=3230 m/s，纵波声速 νl=5950 m/s，声阻抗Z1=4.58×107Pa·s/m3.相邻两种介质的声阻抗相差5个数量级.

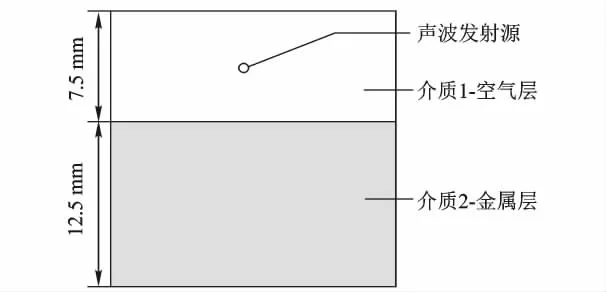
图2 仿真模型示意图

由于计算机容量限制，FDTD技术只能在有限区域进行，因此边界将采用完全匹配层(PML，Perfectly Matched Layer)方法进行处理［2］.

按照仿真空间间隔远小于超声波在被检试件中传播波长的要求以及仿真时间间隔根据Courant限制条件选取的方法，取空间间隔h=50μm，时间间隔T=5 ns.当采用常规FDTD方法进行声场模拟时，仿真程序运行一段时间后，便出现图3所示现象，仿真程序无法继续进行.

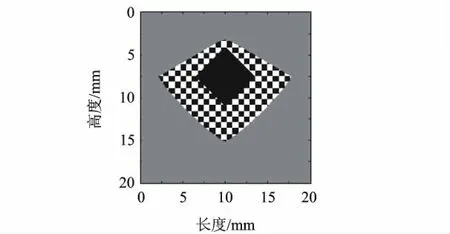
图3 利用常规有限差分法计算的声场图

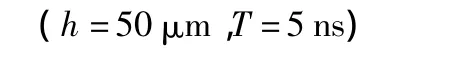
在相同空间和时间间隔下，采用改进的FDTD方法进行声场模拟时，程序运行正常，如图4所示.可见，改进的FDTD方法保证了差分计算的稳定性.

图4 利用改进有限差分法计算的声场图

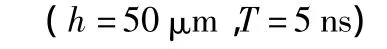
在牺牲仿真时间的情况下，将计算参数的空间间隔和时间间隔均缩小5倍，即空间间隔h=10 μm，时间间隔T=1 ns时，采用常规FDTD方法再次进行声场模拟，仍出现图3所示发散现象.采用改进的FDTD方法进行声场模拟，程序正常运行.

上述数值仿真实验表明，当相邻两种介质的声阻抗相差较大时，即使采用Courant条件选取适当的空间和时间间隔，甚至将空间和时间间隔缩小5倍的情况下，仍会引起差分计算的不稳定.而采用改进的FDTD方法时可以有效解决发散现象，保证了差分计算的稳定性.

3 FDTD改进方法的正确性验证

3.1 仿真实验

设计如图5所示的检测试样，试块中纵波声速5 900 m/s，横波声速 3 230 m/s，密度 7 900 kg/m3.

按照图5所示建立仿真模型，仿真参数:空间间隔h=0.1 mm，时间间隔T=10 ns.激励信号为1个周期2.5 MHz的正弦信号.

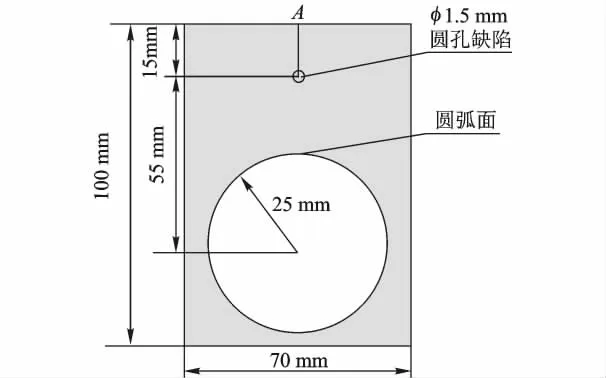
图5 检测试样

在试样上表面中心位置处(图5中A点)激励信号，图6所示为某时刻的声场空间分布情况.取应力来表征回波信号幅值，并做归一化处理，所获得的信号A型图如图7所示.

图6 超声声场分布图

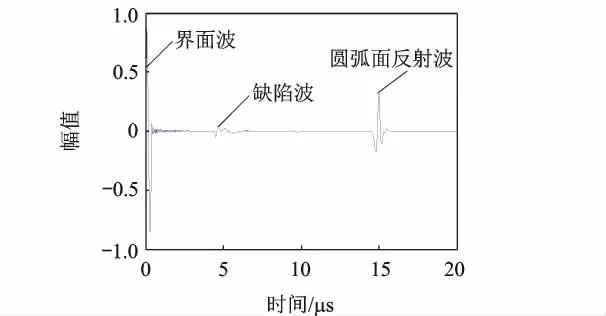
图7 仿真信号A型图

3.2 检测实验

采用单晶探头检测试样，探头中心频率2.5 MHz，直径20 mm，采用接触法检测.当探头放于试样中心位置时，超声信号A型图见图8.

对比图7和图8，仿真和实验的结果均可识别出试样上表面的界面波、缺陷波和圆弧面反射波，且时间位置与理论值一致.

仿真与检测结果表明，改进的有限差分算法可以用于超声检测的数值仿真.

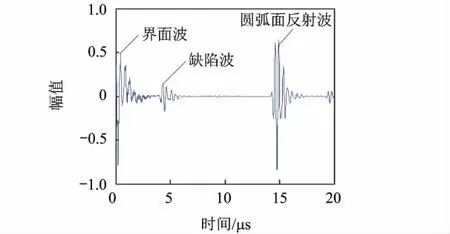
图8 实验信号A型图

4 结论

1)FDTD的改进方法有效解决了相邻两种介质声阻抗相差较大时的算法稳定性问题;

2)FDTD的改进方法能够用于弹性固体中超声波传播的仿真计算，是超声波声场特性分析的一种有效数值方法.

References)

［1］丁辉.计算超声学-声场分析及应用［M］.北京:科学出版社，2010:1-9 Ding Hui.Computational ultrasonics-analysis application of ultrasonic field［M］.Beijing:Science Press，2010:1-9(in Chinese)

［2］魏东，周正干.固体中脉冲超声波传播的有限差分模拟［J］.航空学报，2010，31(2):388-392 Wei Dong，Zhou Zhenggan.Finite difference simulation of pulsed ultrasonic propagation in solids［J］.Acta Aeronautica et Astronautica Sinica，2010，31(2):388-392(in Chinese)

［3］ Satyanarayan L，Sridhar C，Krishnamurthy C V，et al.Simulation of ultrasonic phased array technique for imaging and sizing of defects using longitudinal waves［J］.International Journal of Pressure Vessels and Piping，2007，84:716-729

［4］ Zhen Fenghua，Chen Zhizhang，Zhang Jiazong.Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method［J］.Microwave Theory and Techniques，2000，48(9):1550-1558

［5］ Schroder C T.On the stability of the FDTD algorithm for elastic media at a material interface［J］.Transactions on Geoscience and Remote Sensing，2002，40(2):474-481

［6］ Thoma P，Weiland T.Numerical stability of finite difference time domain methods［J］.Magnetics，1998，34(5):2740-2743

［7］ Remis R F.On the stability of the finite-difference time-domain method［J］.Journal of Computational Physics，2000，163(1):249-261

［8］ Pereda Jos'e A，Oscar Garc'a，Angel Vegas，et al.Numerical dispersion and stability analysis of the FDTD technique in lossy dielectrics［J］.Microwave and Guided Wave Letters，1998，8(7):245-247

［9］李太宝.计算声学-声场的方程和计算方法［M］.北京:科学出版社，2003:67-83 Li Taibao.Computational acoustics-sound field equation and calculate method［M］.Beijing:Science Press，2003:67-83(in Chinese)