基于混沌序列加权抽样和排序变换的图像置乱

曹光辉 胡 凯

(北京航空航天大学 计算机学院，北京100191)

随着互联网和多媒体技术的飞速发展，当今社会已经进入了一个全新的网络化和数字化时代.通过网络传输的多媒体信息防御主动和被动攻击的重要性越来越引起人们的关注.图像作为通过网络传输的主要内容之一，其安全性位列其中.目前，信息加密是保护图像信息的主要手段，但传统的加密技术适用于具有类似单链表结构的普通数据流，图像是一种八连通结构，像素间具有很强的相关性，这种结构的差异，使置乱成为对图像加密预处理的一种重要技术.当然，图像置乱除用于数字图像加密方法预处理外，也常用于更复杂的隐藏与数字水印的预处理或后处理，以增加隐藏和抗攻击能力.目前，已经有多种置乱算法可供选择，例如Baker映射方法［1］、高维Arnold变换和 Fibonacci-Q 变换［2］、Hilbert方法、元胞自动机方法、仿射变换、幻方变换、骑士巡游变换、混沌二叉树遍历方法、混沌位置交换方法［3］、混沌排序方法［4］等，而且新的数字图像置乱算法可能被不断的提出.在这些方法中，混沌排序方法因充分利用混沌非周期、初值敏感等特性，并且算法对混沌数据一次性处理，使用简单，安全性高，被广泛使用，但存在密钥空间不足，置乱度低，易受重构攻击等缺点.为了克服这些不足，本文以一类典型的混沌排序方法——Ye算法［4］为例给予研究.

1 Ye算法流程概述

1)读入图像并且以十进制矩阵A的形式表示，A矩阵大小为M×N;

2)把A矩阵所有元素，都转化为二进制数，形成二进制矩阵B，大小为M×8N;

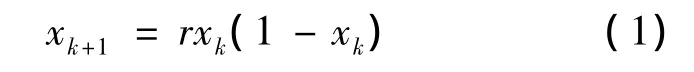
3)利用Logistic方程:生成合适长度的混沌序列X，对该混沌序列进行排序，得到新的序列X1，找到新序列X1中每一个元素在原序列中的位置，生成位置向量，记为T;

4)依据向量T重新排列矩阵B的所有行，生成矩阵B1;

5)类似于步骤 3)，生成位置向量 Vi，i∈［1，M］，每一个Vi，元素个数为8N;

6)依据对应的位置向量Vi，对矩阵B1的每一行元素置乱，得到矩阵C;

7)把二进制表示的C矩阵，以8 bit为一组，转换为十进制表示的矩阵D，置乱过程结束.

2 Ye算法置乱强度分析

为了研究Ye算法置乱强度，首先对如下置乱实例进行实验:生成矩阵A，取Logistic控制参数r=3.65，初值x0=0.55，应用Ye算法，对原始矩阵A以矩阵元素为单位置乱，得到B矩阵.可以看到，B矩阵第2、第3行对应列位置仅有3个元素不同，第4、第5行置乱结果完全相同.结果表明:相邻两行整体模式匹配度高，B矩阵每一列并不是均匀分布，新模式出现的随机性有待改进.为了进一步揭示Ye算法置乱的水平，下面首先设计置乱强度测试算法，然后应用该算法分析Ye算法置乱强度.

目前，置乱强度测试算法很多［5］，主要基于置乱后像素值的某种表现，这些算法不能避免不同位置的相同像素值对置乱强度测试产生的影响.本文为避免置乱强度测试与具体像素值相关，提出如下的设计规则和相应算法.

2.1 设计置乱测试算法原则

1)因为置乱是数据位置的改变，与实际置乱内容值无关，应该致力于衡量被置乱对象相对位置改变的程度;

2)评估应能反映置乱方案的特征.

2.2 置乱测试算法

依据这个原则，设计了针对基于混沌排序置乱算法的均匀随机置乱测试算法，步骤如下:

1)生成大小为m×n的原始测试矩阵A=［ai，j］，其中 A(:，i)=i，i∈［1，n］;

2)应用Ye算法，对矩阵的每一行置乱;

3)统计矩阵每一列包含数字1的数目，2的数目，…，n的数目;

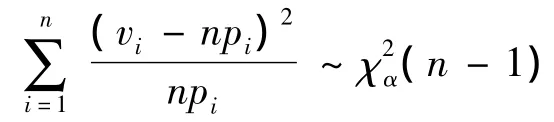
5)计算所有列通过卡方测试比率:η=n0/n×100%，n0为卡方检验接受的次数.

2.3 实验结果

为了与常见256×256图像数据量一致，实验数据量取m=256，n=256×8.应用置乱测试算法，对Ye算法进行测试，实验结果如表1所示.

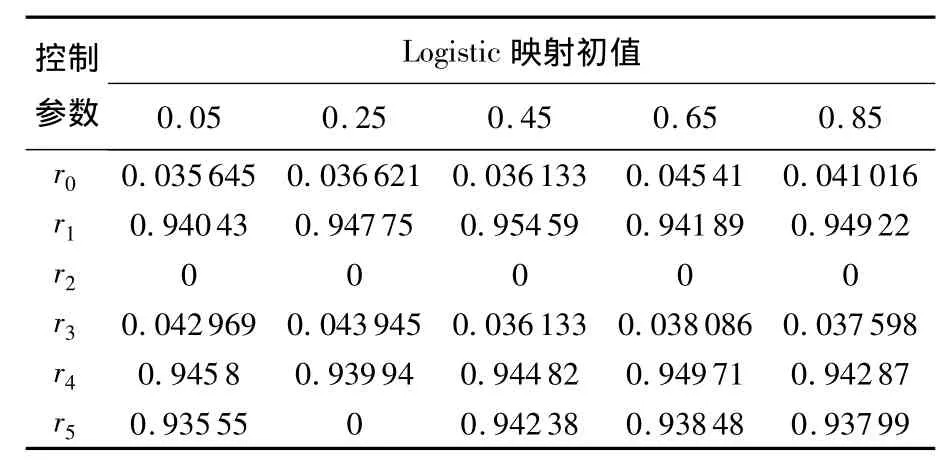
表1 Ye算法置乱强度测试通过率

从表1可见，Ye算法置乱强度主要受混沌控制参数影响.当控制参数一定时，初值对置乱强度造成小范围波动.这些控制参数，有的能使Ye算法具有很好的整体置乱水平，如 r1，r4，r5，有的则使Ye算法置乱水平很低，如r0，r2，r3.如何使基于混沌排序置乱算法的置乱水平不受或少受控制参数影响，成为本文探究的目标.

3 等间隔混沌序列图像置乱

3.1 等间隔混沌序列置乱算法强度分析

Ye算法关键思想是首先产生混沌序列，然后对混沌序列排序，生成位置向量，驱动数据置乱.混沌序列的生成模式决定了数据置乱强度.本文尝试使用基于某种规则，对混沌原始序列抽样，形成新的混沌序列，那么，基于什么样的规则成为本文探究的对象.本文分别探究基于1次、2次、3次间隔抽样的方法生成新的混沌序列，进行排序和置乱，置乱强度测试结果见表2.

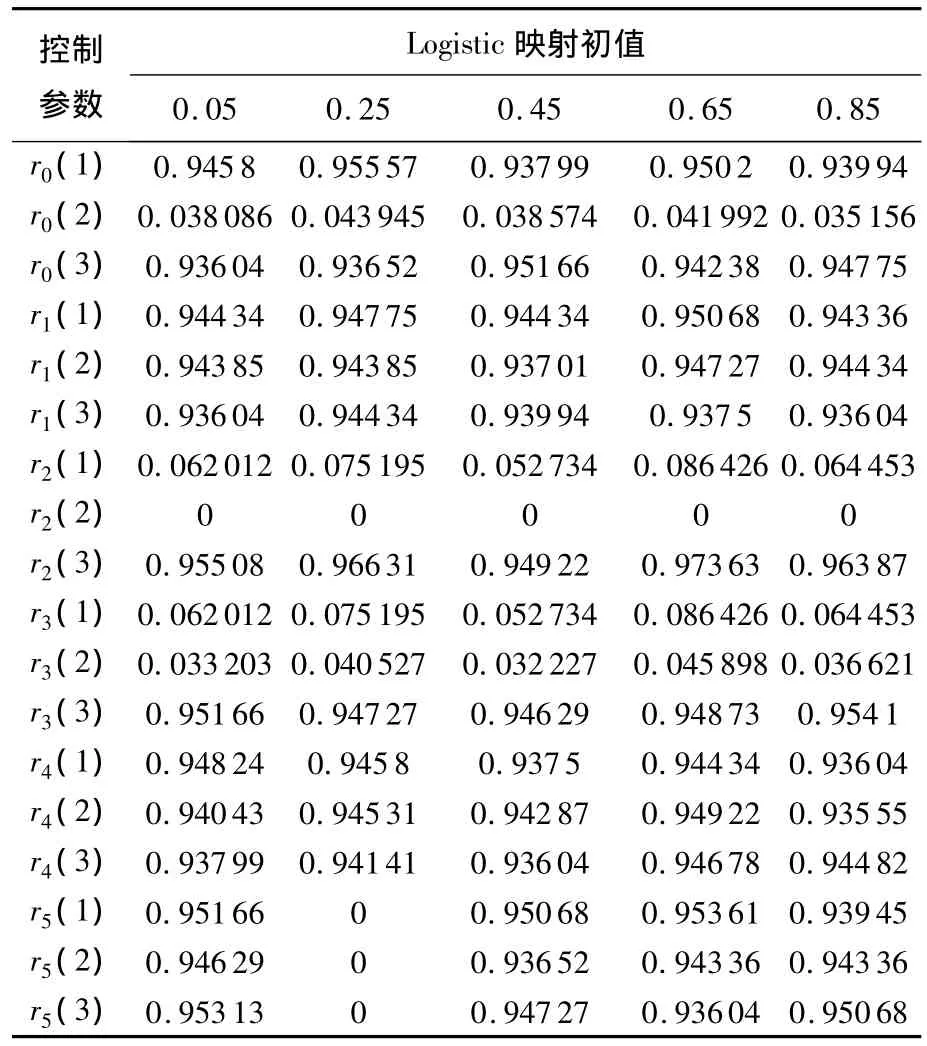
表2 等间隔混沌序列置乱算法置乱强度

从实验结果可见:

1)总体而言，在抽样间隔确定的条件下，Logistic映射参数控制卡方测试通过率的幅度，但不排除个别奇异点(如参数为4.0情况);初值变化对卡方测试通过率幅度造成一定波动.其他m×n×8形状的数据矩阵，也给予实验，得到类似的结果.

2)奇数次间隔抽样产生的混沌序列对原始Ye算法置乱强度测试通过率达到90%的系统，效果不显著，对强度测试通过率低于90%的系统，效果显著提高.对于偶数次间隔抽样形成的置乱系统，强度测试通过率与使用混沌原始序列效果相当.

3)在基于抽样混沌序列排序的图像置乱算法中，影响系统置乱程度的因素从强到弱排序:抽样间隔大小＞系统控制参数＞系统初值.因此，本文建议置乱系统密钥组成为(抽样间隔大小，控制参数，系统初值).

3.2 混沌间隔抽样提高置乱强度的机理

下面采用近似熵方法对混沌序列间隔抽样提高图像置乱强度的原因进行分析.

3.2.1 近似熵理论

近似熵(ApEn)由Pincus于1991年提出，并在度量混沌时间序列复杂性方面得到广泛应用，其主要思想是基于一维序列进行多维相空间的重构，描述维数由m增加至m+1时产生新模式的概率，即表示前一数据对后一数据的可预测性，定量描述时间序列的可重复性、系统运动的复杂性和无序程度，是时间序列结构相似性的度量方法.ApEn值越大，表明时间序列越具有随机性或不规则性，其非周期性越强，复杂度越高;ApEn值越小，表明数据周期性越强，确定性越大，复杂度越小.基于此原理，本文采用近似熵测量混沌序列间隔抽样熵值走势，找出置乱强度增加的内在动力.

3.2.2 实验结果及分析

本文采用经典近似熵算法，分别对基于1次、2次、3次间隔抽样生成的混沌序列，进行近似熵值计算，计算结果见表3.

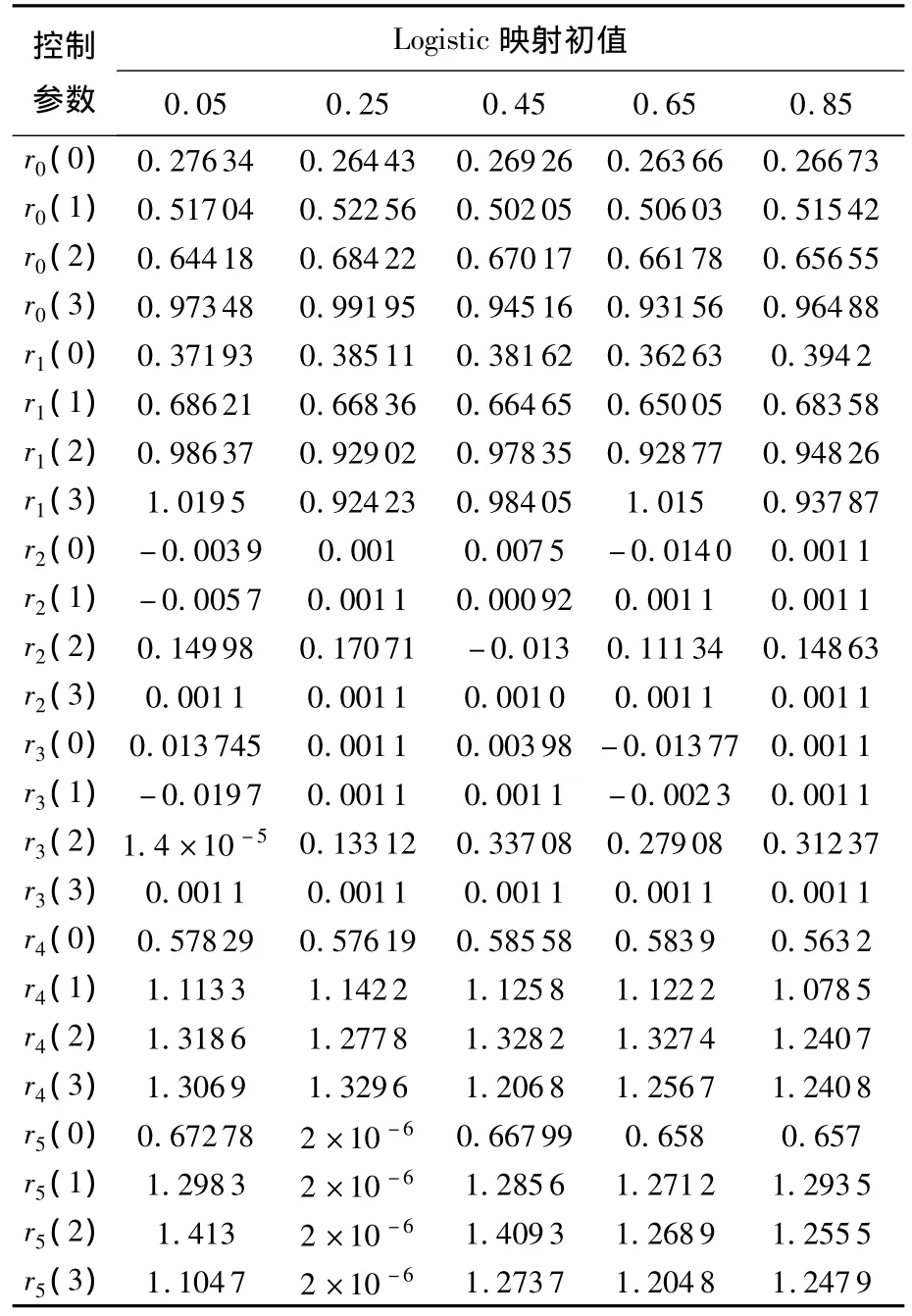
表3 单一间隔混沌序列近似熵分析

近似熵维数m=2，阈值等于0.2倍标准差，抽样得到序列长度1000.

从表3中的实验数据可见，混沌序列间隔抽样能够一定程度提高序列近似熵，在一定范围内，抽样间隔间距越大，近似熵越大.但值得一提的是，虽然偶数次抽样混沌序列能提高近似熵值，但由于混沌序列特有的伸展收缩特性使得形成的二次混沌序列具有明显的大数小数连接模式，这样引入排序后，偶数次间隔抽样混沌序列产生的模式与原始序列产生的模式效果相当.故在基于混沌排序置乱算法中，对图像置乱产生的效果，表现很一般，使用中偶数次抽样间隔产生序列给予忽略.

3.2.3 近似熵走势分析

为了研究近似熵与抽样间隔大小的关系，近似熵走势实验被设计.实验参数如下:图1中Logistic控制参数r=3.75，初值x0=0.85，抽样间隔由0间隔抽样到间隔100次取一次，每个种类间隔抽样1000次;图2中Logistic控制参数r=4，初值x0=0.55，抽样间隔由0间隔到间隔100次抽样一次，每个种类间隔抽样1000次.

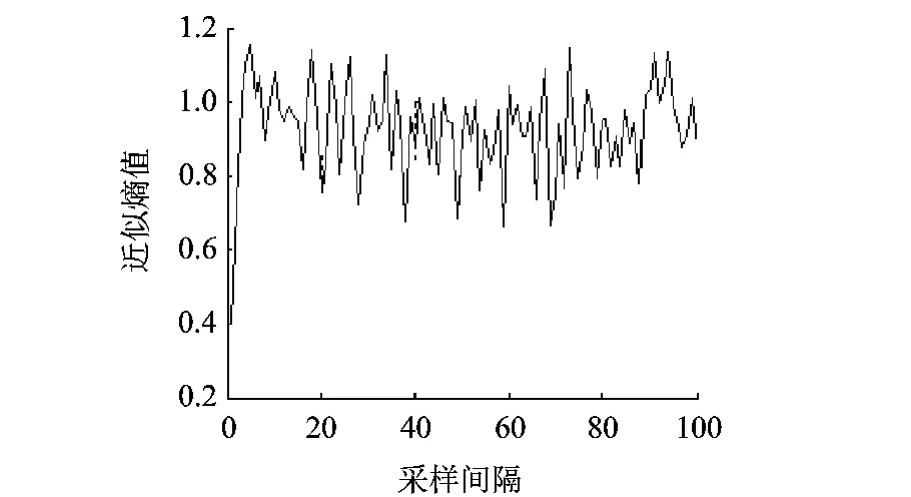
图1 r=3.75近似熵走势

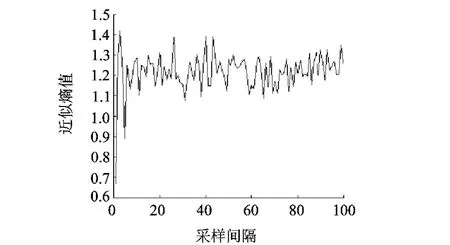
图2 r=4近似熵走势

由图1和图2可见，随着间隔抽样次数的增加，信息熵会在一定范围内波动，但不会一直增加下去.

3.2.4总结

上述实验说明，采用间隔抽样可以提高序列不规则模式出现的概率，进而能够提高置乱强度，同时，近似熵增加到一定值后，随抽样间隔的增加上下波动.这可以解释混沌序列间隔抽样可以提高基于混沌排序置乱算法的置乱强度.

采用单一抽样间隔尽管能够提高置乱算法的置乱强度，但不能提高算法的密钥空间，故本文进一步给出基于加权间隔抽样的图像置乱算法.

4 加权抽样混沌图像置乱

根据对Ye算法置乱强度的定量分析发现，由原始混沌序列抽样后形成新的混沌序列用于置乱数据可以提高置乱强度，故本文设计的置乱系统引入抽样间隔参数.考虑抽样间隔次数的多样性，引入抽样加权机制，由用户指定概率决定每个抽样间隔出现的次数，其中随机源由修正Logistic映射生成［3］.

4.1 加权系统思想

加权保密系统最早由Shannon［6］提出.假设2个保密系统T和R，常用不同的方式形成新的保密系统S.如果T和R具有相同的消息空间，可以形成一类加权和S=pT+qR，这里p+q=1.这个操作首先对概率p和q做出选择，用以决定T和R哪一个被使用.这个选择是系统S密钥的一部分.选择之后，T或R被用作原始的定义.系统S的整个密钥必须指定T和R哪一个系统被使用，以及T或R的哪个密钥被使用.这个加权系统的一般形式如下:

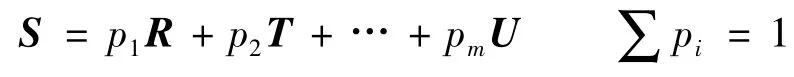
4.2 加权抽样混沌排序图像置乱算法

系统使用2个Logistic映射，一个用于确定混沌序列抽样间隔数，叫修正Logistic映射［3］，方程如下:

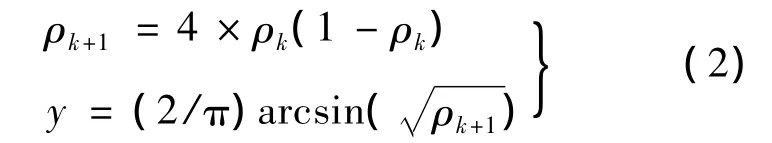
一个用于生成混沌间隔抽样序列，叫主Logistic映射，方程是式(1).

4.2.1 随机抽样间隔的选择

本文使用的加权置乱系统如下:

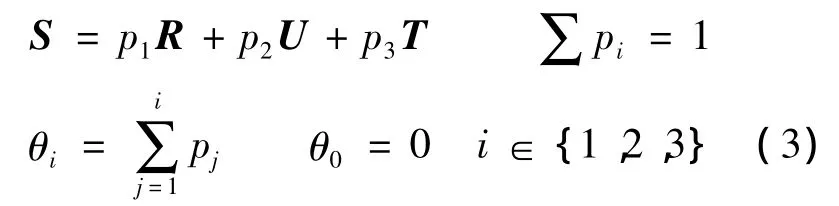
其中，pi由用户指定或系统设定;θi由公式(3)求出.

应用修正Logistic映射，生成随机数ρ，如果ρ∈［θi-1，θi)，则进行与概率 pi对应的间隔抽样.p1对应混沌序列1次间隔抽样，p2对应混沌序列3次间隔抽样，p3对应混沌序列5次间隔抽样.R，U，T使用同一主Logistic映射，区别在于生成不同抽样间隔的混沌序列.

4.2.2 加权抽样混沌序列置乱算法

步骤如下:

1)应用修正Logistic映射生成随机值ρ，根据该随机值，按照4.2.1节确定抽样间隔，使用主Logistic映射生成具有该抽样间隔的混沌随机序列;

2)依据基于混沌排序的数据集置乱算法，应用步骤1)生成的混沌序列对图像进行行置乱;

3)应用修正Logistic映射生成新的随机数，根据该随机数，按照4.2.1节选择抽样间隔，使用主Logistic映射生成具有该抽样间隔的混沌随机序列;

4)依据基于混沌排序的数据集置乱算法，应用步骤3)生成的混沌序列对图像每一行的所有像素比特进行列置乱;

5)重复步骤3)和步骤4)直到图像的最后一行完成为止.

算法框图如图3所示.

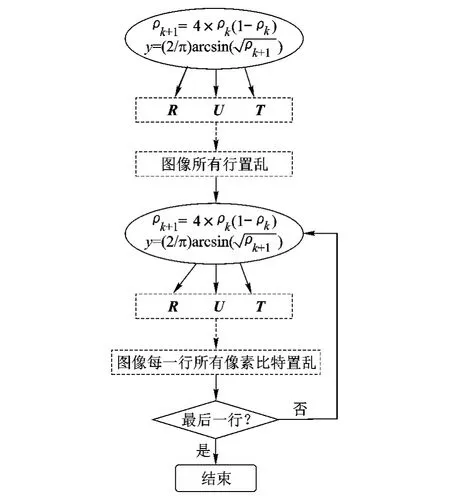
图3 建议算法框图

5 实验结果

为验证本文的算法，对大量各类图像进行了实验，取得了很好的结果.图4给出粗纹理图像的实验结果.

从图像的置乱结果可见，本文设计的加权抽样置乱算法能够很好地打乱原始图像的八连通结构;从置乱图像空间直方图可见，原始图像的相关性被很好地去除，空间分布显示出置乱像素分布的均匀性.这些实验结果表明本文设计的算法达到了打乱原始图像八连通结构，去除相关性的目的，为进一步图像加密和数字水印奠定了很好的基础.

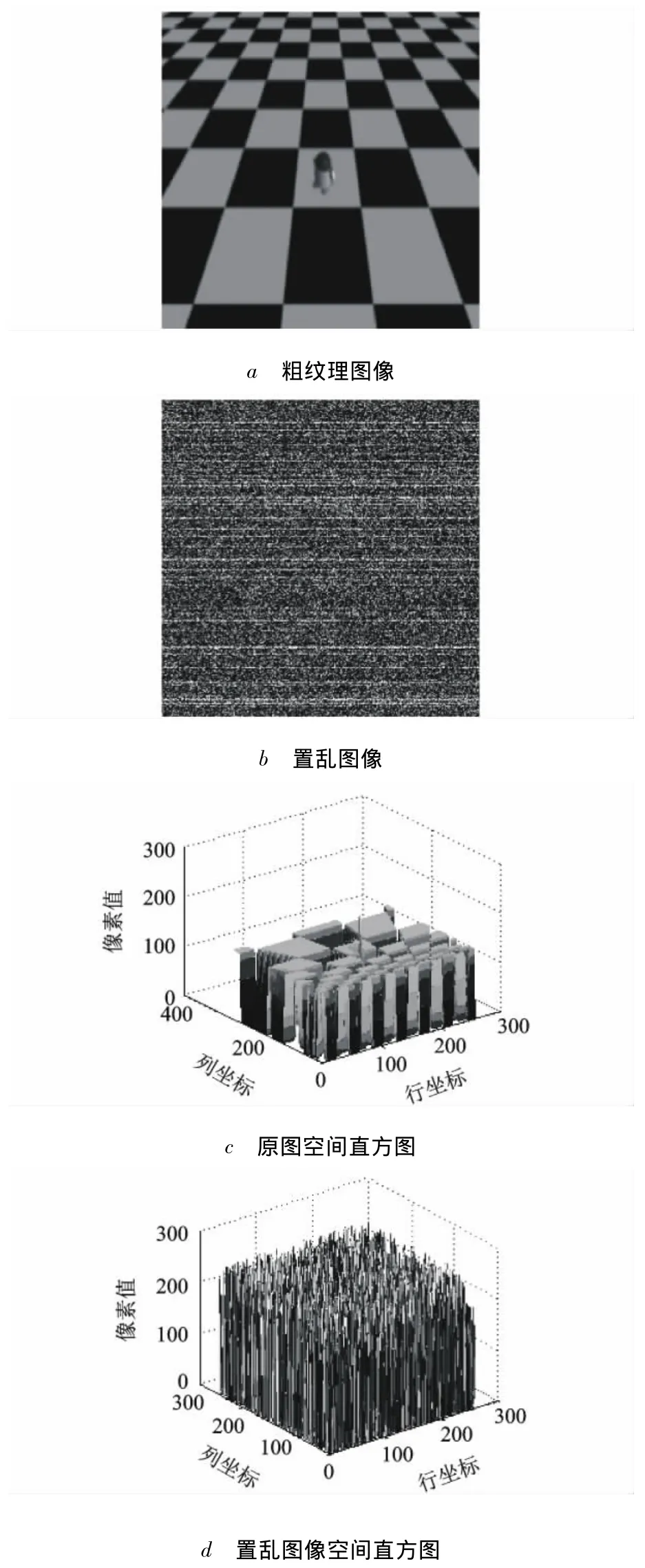
图4 粗纹理图像置乱效果

6 加权抽样置乱算法安全性分析

6.1 密钥空间

本文建议的图像置乱系统应用2个Logistic映射方程，一个是产生混沌均匀分布序列的修正Logistic映射，用于按用户指定的概率选择混沌抽样间隔的大小，一个是依据选择的抽样间隔生成混沌序列用于置乱图像.因此，密钥空间为2个Logistic方程的初值，2个控制参数，以及概率pi的选择.与Ye算法比较，密钥空间是原来的2倍多.

6.2 抗重构攻击

利用混沌进行图像置乱存在重构攻击的可能.相空间重构的基本思想是一个结构复杂的系统可以用相空间中的吸引子来描述.Takens从理论上给予证明，并提出了著名的嵌入定理.

从该定理可知，已知的观测序列是等间隔采样，如果是不等间隔采样，定理不成立.结合本文用于置乱图像的混沌序列，可分为2种情况讨论:

1)当攻击者获得的观测序列是非等间隔采样序列时，依照嵌入定理恢复出的动力系统是错误的，无法进行相空间重构.

2)当攻击者获得的观测序列是等间隔采样序列时，合理选择嵌入维数m和延迟时间τd，应用文献［7］理论上可以恢复原非线性动力系统，但依照等间隔生成的混沌序列破解置乱图像是失败的，因为本文设计的是混沌非等间隔抽样序列置乱图像，混沌抽样序列间隔依靠另一个系统产生的概率决定，并不是使用闭合混沌迭代序列驱动图像置乱.另外，由于本文使用间隔抽样混沌序列，当间隔长度使抽样序列成为欠采样序列时，依据文献［8］可知，混沌序列预测能力大大降低，是否能够进行相空间重构目前还没有相关研究.

综上所述，本文设计的图像置乱系统具有抗重构攻击的能力.

6.3 加权间隔抽样置乱算法置乱强度分析

表4给出应用本文设计的置乱强度测试算法对加权抽样混沌置乱图像算法进行置乱强度测试的实验结果.

比较表1和表4的实验结果可见，本文建议的图像置乱算法的置乱强度远远优于Ye算法的置乱强度，进一步证实了加权抽样混沌序列能够提高图像置乱效果.

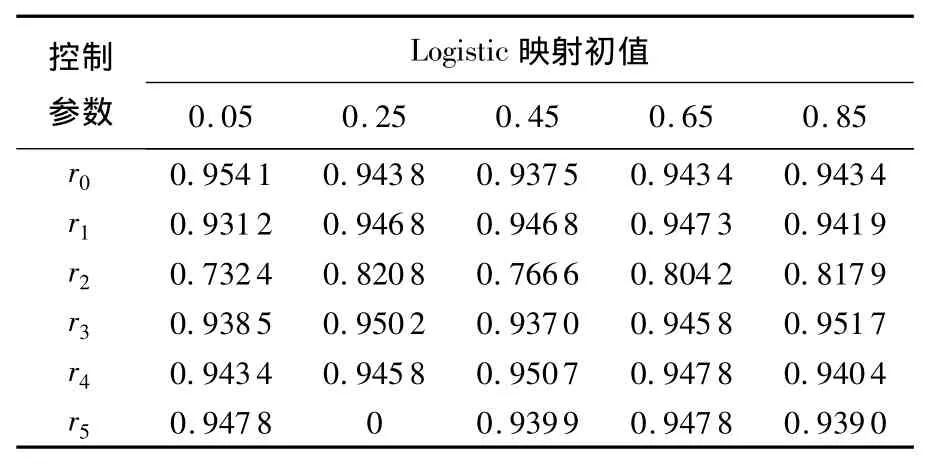
表4 建议算法置乱强度测试

7 结论

基于混沌的图像置乱是当前信息安全领域的一类热点话题.本文研究了一类典型的基于混沌排序图像置乱算法——Ye算法.首先给出Ye算法的简单描述，然后针对该算法，给出与置乱对象无关的置乱强度测试算法.探索发现间隔抽样混沌序列可以提高Ye算法置乱度，并用近似熵给出其理论依据.为增加密钥空间，设计了基于加权采样混沌排序的图像置乱算法，该方法密钥空间大，置乱强度高，抗重构攻击.本文仅针对基于混沌排序置乱算法给出基于位置的置乱强度测试方法，如何设计与置乱对象无关的适合任何图像置乱算法的强度测试算法是作者努力的方向.

致谢感谢Michigan State University的佟维博士与作者的密切交流与合作.

References)

［1］ Fridrich J.Symmetric ciphers based on two-dimensional chaotic maps［J］.International Journal of Bifurcation and Chaos，1998，8(6):1259-1284

［2］ Sun Fuyan，Liu Shutang，Lü Zongwang.Image encryption using high-dimension chaotic system［J］.Chinese Physics，2007，16(12):3616-3623

［3］曹光辉，胡凯，佟维.基于Logistic均匀分布图像置乱方法［J］.物理学报，2011，60(11):110508-8 Cao Guanghui，Hu Kai，Tong Wei.Logistic uniform distribution based image scrambling ［J］.Acta Physica Sinica，2011，60(11):110508-8(in Chinese)

［4］ Ye Gongdong.Scrambling encryption algorithm of pixel bit based on chaos map［J］.Pattern Recognition Letters，2010，31(5):347-354

［5］陈燕梅，张胜元.基于交叉熵的数字图像置乱程度评价方法［J］.中国图象图形学报，2007，12(6):997-1001 Chen Yanmei，Zhang Shengyuan.Digital image scrambling degree evaluation method based on cross entropy［J］.Journal of Image and Graphics，2007，12(6):997-1001(in Chinese)

［6］ Shannon C E.Communication theory of secrecy systems［J］.Bell System Technical Journal，1949，28:656-715

［7］李鹤，杨周，张一民，等.基于径向基神经网络预测的混沌时间序列嵌入维数估计方法［J］.物理学报，2011，60(7):070502-6 Li He，Yang Zhou，Zhang Yimin，et al.Methodology of estimating the embedding dimension in chaos time series based on the prediction performance of radial basis function neural networks［J］.Acta Physica Sinica，2011，60(7):070502-6(in Chinese)

［8］ Barahona M，Poon G S.Detection of nonlinear dynamics in short noisy time series［J］.Nature，1996，381:215-217