浅谈大学物理教学中的相位概念

周 林， 张 亮

(南京晓庄学院 物理与电子工程学院， 江苏 南京 211171)

浅谈大学物理教学中的相位概念

周 林， 张 亮

(南京晓庄学院 物理与电子工程学院， 江苏 南京 211171)

相位是物理学中非常重要的概念之一，理工科大学生在《大学物理》课程中多次接触到这一重要的物理概念，其首次引入是在振动和波动部分。由于相位的概念比较抽象，加上和一些复杂的微积分运算混合在一起，因此构成了大学物理教学中的一个重点和难点。结合多年大学物理教学经验，作者以振动和波中的相位为出发点，系统阐述相位的物理概念，揭示相位的物理图像，以方便学生更好地掌握物理学领域这一重要概念。

振动；波动；相位；旋转矢量

0 引言

相位是物理学中非常重要的概念之一。1918年，赫尔曼·外尔引进了相位因子的概念，试图把电磁学和引力场联系起来，这一理论被称为“规范理论”。1972年，量子力学的奠基人之一狄拉克到他70多岁的时候说：“如果有人问我量子力学的主要特点，今天我会说，不是不可译，而是相位。”著名物理学家杨振宁先生在一次演讲中也提到，21世纪物理学的主题旋律是量子化、对称和相位因子，认为这三个观念的改变、演进、纠缠在一起，造成了20世纪理论物理的主体发展。

事实上，任何有波动观念的理论都有相位的概念。理工科大学生在《大学物理》课程中也要多次接触到这一重要的物理概念，其首次引入是在振动和波动部分[1]。然而由于相位的概念本身比较抽象，加上和一些复杂的微积分运算混合在一起，因此构成了大学物理教学中的一个重点和难点。本文以振动和波中的相位为出发点，系统阐述相位的物理概念，揭示相位的物理图像，以方便学生能更好地掌握这一物理学领域的重要概念。

1 什么是相位

相位，在英语中用phase表示。在物理学中，phase通常有两种翻译：相或相位。前者(相)是表征物质形态的物理量，如人们熟知的物质存在形态的固、液、气态，亦即固相、液相和气相；后者(相位)则是表征波的一个重要物理量。相位，又称位相，是某一物理量随着时间(或位置)作余弦(或正弦)变化时，决定该量在任一时间(或位置)状态的一个数值。对于一个波而言，相位反映了在特定时刻波在其周期循环中的位置，是一种它是否在波峰、波谷或它们之间的某点的标度，也是描述讯号波形变化的度量，通常以度(角度)作为单位，也称作相角。当波形以周期的方式变化时，波形循环一周即为360°。常应用在科学领域，如数学、物理学等领域。

2 振动和波动问题中的相位概念

在大学物理课程的教学中，涉及相位概念的章节有多处，而首次出现是在振动和波动部分。下面，我们从振动的运动学描述、振动和波动的关系、平面简谐波波动方程三个方面对相位的概念进行深入的剖析，以期寻找相位在波动问题中的物理图像和意义。

2.1 从振动的运动学描述看

大学物理课程中涉及机械运动的三种基本的运动形式：平动、转动和振动。其中，站在长时间的角度进行观察，转动和振动都具有典型的周期性、不断重复的特征，而在一个时间周期内观察每一个运动状态又都是独一无二、不可重复的。

以地球公转为例，其周期一般为365天。每一天都可视为一个不同的运动状态，于是有春夏秋冬，二十四节气，年复一年，四季循环。从物理学的观点来看，这就是一个典型的相位概念。缩短到一个月来看，也是如此。所以，月亮的阴晴圆缺实际上是月亮的相位(月相)。

从振动和转动运动形式的相似性可以推测振动也应该有相位特征。实际也是如此。更为有趣的是，在最简单最基本的振动形式——简谐振动的运动学描述中，还能给出相位的定量表述。大学物理教程系统介绍了两种最简单的简谐运动：弹簧振子和单摆。无论哪一种，其运动学方程都可以写成如下形式的通解：

x(t)=Acos(ωt+φ)

(1)

公式(1)是简谐运动的运动学描述法之一——数学解析描述法[2]。式中，x(t)表示简谐振子的位移(角位移)，ω表示振动圆频率，由振动系统自身的特征所决定。A和φ是求解动力学微分方程所产生的两个积分常数，其中A表示振动的振幅，反映初始注入系统的能量的大小；φ的引入能够把计时零点(t=0)时刻不同的初始状态所导致的不同简谐运动区分开，被称为初始相位[3][4]。故φ(t)=ωt+φ表示t时刻简谐振子的相位。

然而，在教学过程中我们发现，仅仅从数学公式上强调φ(t)=ωt+φ是谐振子的相位，大多数同学并不能很好的理解和掌握。这得在简谐运动的特征上找原因。前面讲到转动和振动都是周期性运动，然而在相位概念的理解上后者却要难得多。其原因是地球公转时，总是以同一运动方向通过路径上的某一点，一个周期内的不同的相位点在空间上完全分开；而(简谐)振动必须有(线性)回复力，这就决定了振子通过某一点的方向总是交替的变化，两个不同的相位点在空间上是重叠的。为了进一步建立相位的物理图像，我们看一下简谐运动的运动学描述方法二——旋转矢量法。

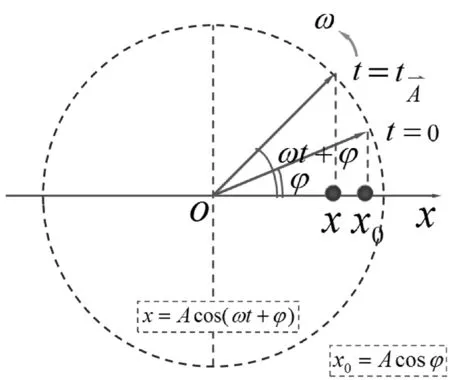
图1 旋转矢量法示意图

图1是旋转矢量法描述简谐运动的示意图。本质上而言，旋转矢量方法是巧妙地利用了转动描述相位的便利性来描述简谐振动[5]。当把一维方向上的简谐振动看成是二维平面内的圆周运动在某一方向上的运动分量(如矢量端点在x轴上的投影点的运动)时，不同的振动状态则可以在空间上完全分开，而在运动学方程中原本很抽象的相位表达式φ(t)=ωt+φ也同时找到了清晰的图像上的对应：任意时刻的相位φ(t)是代表该时刻运动状态的旋转矢量与x轴方向的夹角。换句话说，每一个简谐运动状态对应一个[0,2π)内的一个角度，对应一个确定的相位。

2.2 从振动和波动的关系看

在大学物理学机械振动和机械波部分，振动和波动的关系是：振动是激发波动的波源，而波动是振动形式在弹性介质中的传播过程。以弹性绳上的横波为例，波的传播可以理解为振动状态的传播，我们可以从以下四个方面理解：1)媒质中各质元并未“随波逐流”；2)沿着波的传播方向看，“上游”的质元依次带动“下游”的质元振动；3)某时刻某质元的振动状态将在较晚时刻于“下游”某处出现；4)有些质元的振动状态相同，它们称作同相点。而最近邻的同相点在波传播方向的空间间隔正好是一个波长。

事实上，由简谐振动的运动学描述可知，质点的振动状态可以用相位唯一描述，沿着波传播路径上弹性介质内的任意一个质点的任意一个振动状态必然能在[0,2π)内找到唯一的一个角度(相位角)与之对应。因此，波的传播又可以理解为相位的传播：1)某时刻某点的相位将在较晚时刻重现于“下游”某处；2)沿波的传播方向，各质元的相位依次落后；3)最近邻的同相点的空间间隔是一个波长，而它们的相位间隔正好是2π。

2.3 从平面简谐波波动方程看

在均匀无吸收的各向同性介质中传播的平面简谐波的波动方程[6]可以写为：

Acos(ωt-kx+φ)

(2)

式中，圆频率ω表征平面简谐波传播的时间周期性，波数k和波长λ表示平面简谐波传播的空间周期性。从数学形式上，公式(2)给出的是在任意时刻t、位于平面简谐波传播路径上任意位置x处的质点作简谐振动的运动学方程。因此，对于一个确定的位置x0，yp(x0,t)代表平衡位置为x0的这个质点在时间轴上的简谐振动的“微电影”；而对于一个特定的时刻t0，yp(x0,t)则表示(空间上)所有质点的振动状态(相位)的一个“合影”。

值得一提的是，这种振动状态的相位本质还体现在平面简谐波传播的时间和空间特性的关联上。在公式(2)中，我们令平面简谐波传播的相位为常数φ0，即：

φP(x,t)=(ωt-kx+φ)=φ0

(3)

其物理意义是：相位φ0在不同时刻出现在不同位置，我们只观察相同相位(φ0)对应的振动状态的传播情况。对公式(3)两边取全微分，得：

d(ωt)=d(kx)

(4)

由于介质均匀无色散，公式(4)即可化简为：

(5)

式中，u表示平面简谐波的传播速度(波速)。这说明，平面简谐波在均匀弹性介质中的传播本质上就是等相位面的传播，因此，波是振动状态的传播和波是相位的传播二者是等价的，而波速u自然也被称为相速度。事实上，相速度u正好是时间周期和空间周期联系的纽带：

(6)

3 总结和讨论

基于以上的讨论我们得出结论，从经典物理的观念来看，相位往往与周期运动联系在一起，如果没有周期运动，也就没有相位。相位正是用来描述一个做周期性运动的物体在一个周期内所处的不同运动状态的物理量，它可以量化为[0,2π)内一个唯一的相位角。这种量化使得周期性运动的描述更为简洁方便。这里需要特别强调的是，相位的取值是具有随意性的。换句话说，选取一个2π长度的区间来描述一个周期内的所有运动状态并不是唯一的，所以读者在一些教材或参考书目中可能看到取[-π,π)的情况，也是合理的。

最后，值得一提的是，前面我们主要讨论的是某一个周期运动的绝对相位，但实际中往往当涉及两个(多个)周期运动叠加时更有意义，此时周期运动之间相位差(或步调差)对叠加之后的合运动起着至关重要的作用。这也是波动光学中波场干涉的物理基础。所以说，相位(特别是相位差)也是干涉现象最重要的物理参量。正确理解相位的概念，对于大学物理课程诸多章节的学习都具有重要的指导意义。

[1] 文蔚.物理学教程[M].北京:高等教育出版社,2002：23-25.

[2] 赖莉飞.浅谈简谐振动中初相位与三角函数的统一[J].浙江万里学院学报，2008(2).

[3] 梁莎莎，刘劲.合振动的初相位确定方法[J].陕西建筑,2010(1).

[4] 刘国跃.简谐运动的相位[J].中学物理，2008(2).

[5] 王慧娟，管永精，刘奕新.旋转矢量法在简谐振动教学中的应用[J].渤海大学学报：自然科学版，2009(2).

[6] 杨百愚，冯大毅，张崇辉，冯明德，马华.如何“写”出平面简谐波的波函数[J].物理与工程，2008(5).

2013-05-20

江苏省高校2012年度青蓝工程优秀青年骨干教师培养项目(2012.12-2015.12)

周林(1981-)，女，湖北随州人，讲师，理学博士，主要从事表面等离激元光子学研究。

O4

A

1671-6876(2013)03-0269-03

[责任编辑王荣江]