具有负系数一致凸函数类子集的卷积性质

陈建兰

(南通航运职业技术学院 基础教学部, 江苏 南通 226010)

具有负系数一致凸函数类子集的卷积性质

陈建兰

(南通航运职业技术学院 基础教学部, 江苏 南通 226010)

解析函数; 一致凸; 分式算子; 卷积; 积分变换

0 引言

利用Hadamard积可以定义分式算子,再利用分式算子可以得到单位开圆内解析函数类的新子集,研究了各类分式算子定义的解析函数类的新子集[1-4],并研究了它们的包含关系,卷积性质,系数估计等.本文利用Hadamard积定义了分式算子Iλ,μ,并由此定义了具有负系数的一致凸函数类的新子集,主要研究了该子集的卷积性质,并讨论了在积分变换Vλ(f)的作用下新子集的特征性质.

若函数f(z),且满足TS(λ,μ,α),其中

则称f(z)属于α阶一致凸函数类[6],记为UCV(α).

若f(z)满足

则称f(z)属于α阶一致星像函数类记为Sp(α).显然,Sp(α)是UCV(α)子集,且有f(z)∈UCV(α)⟺zf′(z)∈Sp(α).

对于f∈A,定义算子Dλ:A→A,满足

这就是著名的Ruscheweyh导数,很多学者对其进行了深入的研究[7-8].

受Ruschewey导数的启发,我们定义算子

Iλ,μ:A→A:Iλ,μf(z)=fλ,μ(z)*f(z),

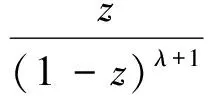
其中(λ)n是Pochhammer符号,定义如下:

显然,当λ=0,μ=1时,Iλ,μf(z)=f(z);当λ=0,μ=2时,Iλ,μf(z)=zf′(z).

利用分式积分算子Iλ,μ我们定义A的一个新子类Sλ,μ(α).

定义1 对于-1≤α<1,若f(z)∈A且满足

其中λ>-1,μ>0,则称f(z)∈Sλ,μ(α).

现在我们定义函数类TS(λ,μ,α)=Sλ,μ(α)∩T.本文主要研究了函数类TS(λ,μ,α)的卷积性质.

定义函数fj(z)(j=1,2,…,m)形如

(1)

引理1[9]若f(z)∈T,则f(z)∈TS(λ,μ,α)的充要条件是

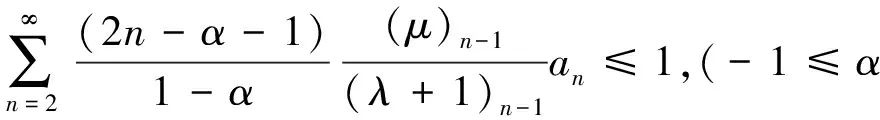
1 主要结论

定理1 设函数fj(z)(j=1,2)由式(1)给出,且f1(z)∈TS(λ,μ,α),f2(z)∈TS(λ,μ,β).μ<1+λ,则f1*f2∈TS(λ,μ,ξ),其中

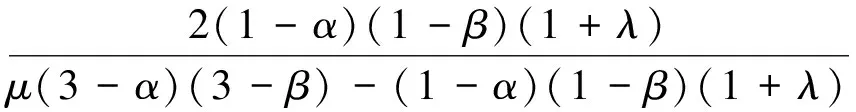
(2)

证明由引理1可知,要说明f1*f2∈TS(λ,μ,ξ),只需说明

其中ξ由式(2)给出.因为f1(z)∈TS(λ,μ,α),f2(z)∈TS(λ,μ,β),则由引理有

则由Cauchy-Schwarz不等式有

(3)

从而我们只需找到ξ满足

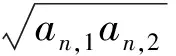
而由式(3)不难看出,可选择适当的n满足

由此可计算出

因为μ<1+λ,从而可取n=2,

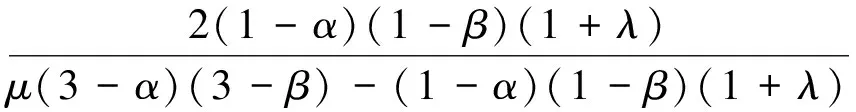
从而定理得证.

推论1 设函数fj(z)(j=1,2)由式(1)给出且fj(z)∈TS(λ,μ,α),μ<1+λ,则f1*f2∈TS(λ,μ,ζ),其中

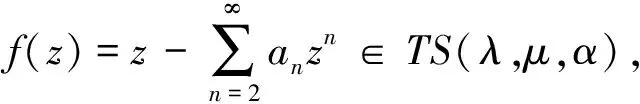
(f*g)(z)∈TS(λ,μ,α).

证明因为|bn|≤1,则由引理1可知

则(f*g)(z)∈TS(λ,μ,α),定理得证.

证明由引理1可知,要证明结论成立,只需要说明

(4)

因为fj(z)∈TS(λ,μ,α),则由引理1有

从而可得

则由上式可知,要想式(4)成立只需满足

即如果δ满足

即式(4)成立.因此,我们取最大的δ,即令n=2,可得

从而定理得证.

定义积分变换

定理4 设f(z)∈TS(λ,μ,α),则Vλ(f)∈TS(λ,μ,α).

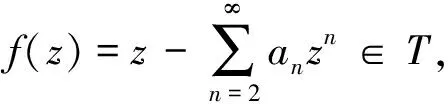
计算可得

由引理1可知,我们仅需证明

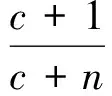
从而定理得证.

[1] Yang D G, Liu J L.On Sakaguchi Functions[J].International Journal of Mathematics and Mathematical Sciences,2003,26,1923-1931.

[2] Liu J L. Some Applications of Certain Integral Operator[J].Kyungpook Mathematics Journal,2003,43,211-219.

[3] Liu J L. A linear operator and strongly starlike functions[J].Journal of Computational and Applied Matematics,2002,54,975-981.

[4] 陈建兰,韦叶,刘金林. 由算子定义的解析函数的卷积性质[J].扬州大学学报:自然科学版,2006,9(4):4-6.

[5] Silverman H. Univalent functions with negative coefficients[J]. Procject of Amercian Mathematics Socity.1975, 51: 1091-116.

[6] Ning F R. Integral representations for bounded starlike functions[J]. Computers and mathematics with applications, 1995, 60: 289-297.

[7] Liu J L. Certain integral operator and strongly starlike functions[J]. International Journal of Mathematics and Mathematical Sciences, 2002, 30: 569-574.

[8] 程艳莉, 刘金林. 一个线性算子及其相关的亚纯多叶函数类[J].扬州大学学报:自然科学版,2004,7(2):10-12.

[9] 陈建兰. 由分式积分算子定义的一致凸函数类的子集[J].盐城工学院:自然科学版,2013,26(1):18-20.

ConvolutionPropertyofaSubclassofUniformlyConvexFunctionswithNegativeCoefficients

CHEN Jian-lan

(Basic Teaching Department, Nantong Shipping College, Nantong Jiangsu 226010, China)

Making use of a linear operatorIλ,μ,which is defined here by means of a Hadamard product,we introduce a new classTS(λ,μ,α) of uniformly convex functions with negative coefficients defined by using a certain fractional calculus operatorIλ,μ. In this paper, we discuss the convolution property of the classTS(λ,μ,α) and integrals transform is discussed

analytic functions; uniformly convex; hadamard product; integrals transform

2013-04-25

陈建兰(1981-), 女, 江苏如皋人, 讲师, 硕士, 研究方向为基础数学.

O174.51

A

1671-6876(2013)03-0199-05

[责任编辑李春红]