“中国 美国 新加坡”小学数学教材中的“分数定义”

蒲淑萍

（1.重庆师范大学 初等教育学院，重庆 401331；2.华东师范大学，上海 200241）

1 研究背景

大量研究表明，分数教学有诸多的障碍与困惑[1～2].原因在于分数是儿童第一次学习数学中有关两个量的相对比较关系，且分数具有多重意义（如部分/全体、集合、数线意义、商、比例等）、多重子概念（如单位概念、等分概念等），而这些子概念又牵涉“连续量”与“离散量”的不同情境，并具有一些特殊的性质，如：等值、稠密性等[3]，因此学生在学习分数概念时需要经历漫长且艰苦的发展过程[4].Kieren提出：教师有必要掌握分数的各种意义，并以各种意义为基础设计分数问题，将有助于发展并考量学生对分数概念的认知[5].

当前在各种国际数学成绩测试中，如TIMSS，PISA，IEA等，中国、新加坡的学生成绩位居前列，而美国的数学学业成绩则一直处于后面几位.然而进一步的调查也发现，位居前列的新加坡、中国的学生对于数学学习的自信心、兴趣等的调查结果却大相径庭，而美国学生成绩虽不尽如人意，但学生对数学的信心、兴趣以及创造力等方面却明显优于中国[6].通过与别国对比，分析比对各自的优势与不足，相互借鉴，寻找东西方数学教育优势互补的中间地带已成为主流趋势.探究、分析新加坡、美国的数学教育，可为中国的数学教育提供参照、借鉴.

教材是影响学生学业成就的关键要素之一.那么对于“分数”这一被各国视为难点的教学内容，中、美、新加坡三国教材是怎样处理的呢？怎样的呈现方式与教学顺序更符合学生的认知？对此，以3个国家教材中的“分数定义”为突破口进行对比研究，他山之石可以攻玉，希望能为中国小学数学教材编写与课堂教学提供借鉴.

2 教材选取与研究问题

学生对分数内容的学习困难，在很大程度上可归结为对分数意义或定义的不明所造成的.研究拟从教科书层面出发，以中国、新加坡、美国的小学数学主流教材：中国的人教版[7～9]，新加坡的Discover Maths[10～14]，以及美国加州小学数学教材California Mathematics[15]三套教材，选取各自教材中“分数定义”内容进行详细的案例研究.中国、新加坡、美国3国的小学均为6年制，中国和新加坡的教材都是每个年级两册，共12册；美国加州则是每个学年一册，共6册教科书.3个国家小学数学教材中都有分数内容，且都是采取螺旋上升的方式设置.因此就分数定义而言，3个国家的教材具有可比性.

对于教材中的分数定义主要关注两个方面：

（1）各国教材中出现了哪几种分数定义？它们的呈现顺序是怎样的？

（2）几种定义采用了怎样的表征形式？定义之间的联系是怎样的？

3 研究方法

研究主要采用“内容比较、分析法（Content analysis）”，这种方法是研究教科书常见的方法之一.因三地教材所用纸张大小、使用文字的差异等，仅从内容所占页码的多少等表层“量”的比对并不能反映三地教材的本质差异.故而，本研究主要采用定性分析的方法，对内容进行深入地、多维度地比对、分析，以此为基础进行解释与推论.比较分析的内容主要包括：（1）各国教材中出现的定义种类及呈现顺序；（2）各类定义的表征形式及各种定义之间的联系.

4 结果及分析

4.1 各类定义及呈现顺序对比

4.1.1 分数定义

关于分数定义，张奠宙、吕玉琴、Kieran等都进行过研究，通常认为分数定义建立在以下4种意义的基础之上，各种意义最后均连接至分数最核心的“除的意义”.①平分的意义：从平分入手学习分数，是一条比较容易的途径，也比较容易化解分数学习中常见的认知冲突；②测量的意义：为解决测量时不足一个单位度量长度时的问题，通常就会引出分数或小数；因为强调单位，故而，测量是调和“部分/全体”的意义与带分数认知冲突中的重要工具；③比例的意义：比的原理，是一种微妙的平分方式，因此学生比较容易接受.比值的引入，让分数具有解决比例问题的意义；④部分/全体的意义：是分数的重要意义之一，但是由于概念较为抽象，而且真分数的暗示过深（整体为1），可能造成假分数或带分数学习上的困扰，必须透过单位的强调来解决其认知冲突.

尽管学者们对分数所下定义不同，但大致可归纳出，出现在小学教材中的分数定义大致有如下4种，分别为：份数定义—部分/整体（包含子集/集合）关系、数线定义（数线上一点）、商的定义（整数相除）、比/比值（部分/部分）.而且在设置顺序上，他们均认为分数的定义在不同的学龄阶段有着不同的内涵，也就是，随着人们对分数认识的不断深入，分数定义的内涵不断拓展，逐渐抽象化.

3个国家小学数学教材中分数定义是怎样呈现的呢？

4.1.2 三个国家小学教材中的分数定义

3个国家教材均对分数的多重意义有所体现，但各种定义呈现时间及顺序有所不同，各类定义之间联系亦不相同，具体见表1.

表1 “中国 美国 新加坡”小学数学教材分数定义的比较

4.1.3 对结果的分析

相同之处：

（1）4种“定义”都在三国教材中出现；

（2）都以“份数定义”为主；

（3）都是呈螺旋上升的方式；

（4）在份数定义中，都是按照从平分开始，介绍单位分数，再到一般分数，真分数、假分数的顺序；

（5）三国教材对除“份数定义”以外的各类定义均采取了“模糊”处理，没有明确说法，只有一些描述性语言，如分数“商的定义”，在3个国家教材中，都没有出现“分数是整数q除以整数p（p≠0）所得的商”这样明确的说法，而只有“比较分数与除法”发现两者之间关系或“作为商的分数”的提法.

不同之处：

（1）“份数定义”不同的处理方式：分数的“份数定义”在三国教材中，都是分数定义的主要呈现方式，但是相比而言，也有着明显的不同：

①出现时间的不同：美国加州教材的“份数定义”出现最早，在二年级前半段（相当于中国、新加坡分册处理的上册）；新加坡教材次之，出现在二年级下册；中国最晚，在三年级上册出现；

②螺旋的次数不尽相同：从表1中可以看到，完整地介绍“份数定义”，中国只用两次（三上与五下），而新加坡和美国教材则经历3次螺旋上升，才完整呈现；

③在“份数定义”中，最大的不同就是新加坡、美国教材中均是按照“parts of a whole”→“parts of a group”→“parts of a set”的顺序，从3个不同层次逐步给出各类情境下的“部分/整体”的分数定义，而中国教材只有一种提法，就是“整体中的部分”，在相应练习中出现如图1所示问题，使学生通过解决此类问题或多或少感受并理解“集合”意义上的“份数定义”.

图1 中国教材中的处理方式

（2）“除法定义”不同的处理方式：3个国家教材最大的不同体现在对除法与分数关系以及化假分数为带分数的问题处理上.

①中国与美国的教材从平均分配的另外一种方法——除法，引出“作为商的分数”，而新加坡教材则仍从分数的“份数定义”出发引出除法算式与之对应的意义解释；

②在处理利用除法化假分数为带分数的问题上，三国教材虽都是通过具体例题展示：商的整数部分作为带分数的整数部分，余数对应分子，所不同的是，新加坡与美国以明确的方式，采用竖式给出做法及除法竖式与分数各个构成成分之间的对应关系；而中国教材先通过问题“一个半”该如何表示，引出带分数定义，后出示例子展示化假分数为整数（整除的情形）或带分数的做法，通过先将分数化为横式除法，再给出带分数表示的做法.

（3）集中程度不同.

相比而言，中国的分数内容主要集中在三年级上册和五年级下册，而新加坡和美国教材则分散在从二年级开始，跨越二、三、四、五，甚至六年级（新加坡），相比中国的设置，显得分散了许多.

（4）对“数线定义”处理方式不同.

张奠宙先生认为：“在过渡到分数的商定义时，在数直线上对分数作几何解释是非常重要的.”[16]事实上，中国教材却是先出现了“商的定义”后才出现“数线上的表示”.诚如张先生所言：“我国的分数教学，擅长分数的计算，不大注意在数轴上直观地加以表示.”相比而言，对数线定义最为重视的当属加州教材，教材中先后多次用“数线”表示分数，内容涉及“例题”、“练习”、“活动”等栏目，并在五年级上学期教学内容中专门有一节“数线上的分数（Fractions on a Number Line）”作为数学实验内容，引导学生进行探究.

图2展示了新加坡教材中数线出现之前的几何模型，图3展示美国加州教材中“数线上的分数”的探究实验内容.

图2 新加坡教材二（下）中数线出现之前的几何模型

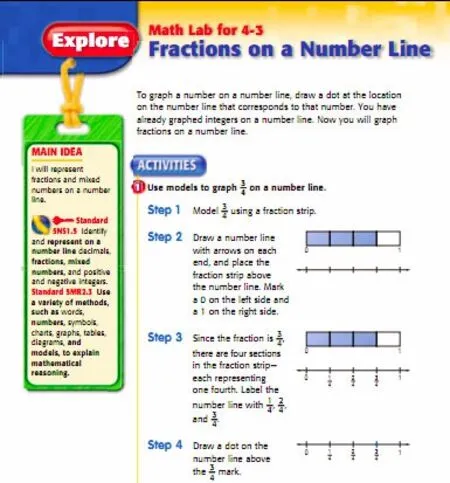
图3 美国加州教材中“数线上的分数”的探究实验内容

4.2 分数定义不同表征形式及其作用

“表征”是学习的重要媒介，也是个体思考与沟通的重要工具，与数学学习有密不可分的关系.表征的功能有：①使数学概念具体化；②可成为沟通的工具；③可成为思考的材料；④可成为解题的工具.Lesh，Post和Behr[17]提到数学学习与数学问题有5种不同的表征，包括现实情境（real-world situation）、操作模型（manipulative models）、图（picture）、口语符号（spoken symbols）及书写符号（written symbols）.在数学学习的过程中，不同的表征对儿童的概念理解产生重要影响，而且也直接影响着问题解决的难易.Behr，Wachsmuth，Post和Lesh[18]强调表征间的转换能力是影响学生数学学习、问题解决及产生、有意义学习的重要因素.通常认为，多种表征形式有助于学生对抽象概念的理解.那么分数定义中的表征形式有哪些？各国在表征形式的选取上是否相同？值得探究.

分数的概念较整数更抽象，而实物和图画式等表征形式更易使学生掌握分数的符号规则.三国教材中，都采用了多种表征形式.这里以分数的“份数定义”这一主要定义形式为例进行比较，希望对中国教材处理抽象概念的表征形式提供一点参考.

可以看到，3个国家“份数定义”中大体都采用了如下4种表征形式：现实情境、具体操作物、图形、符号（教材中主要是书写符号）.因3个国家教材对“份数定义”处理的不同，单从数量并不能说明各自的差异，这里主要对“份数定义”中各类表征形式之间的联系进行比对，发现3个国家教材对定义中表征形式的处理并不相同.

在表征顺序上，中国教材多从具体情境出发，引出问题，借助具体操作物，进而过渡到“图形”表征，在做了这些准备后，给出定义及符号表达.这种处理方式体现了“数学化”的过程及思想；加州教材多是从定义出发，介绍定义及符号表示，后借助具体操作物、图形解决问题，多在后面练习及问题解决中出现与该内容相联系的现实情境，似乎是为寻找知识在生活中的“作用”；新加坡教材则从“折纸”等具体操作入手，给出对应“符号”，再给出相应文字定义.种种做法孰优孰劣，很难直接下结论，在教学中可尝试多种教学设计，探寻更加符合学生认知的表征形式的呈现过程.

5 启 示

5.1 对分数定义处理的启示

5.1.1 份数定义宜分层次处理

相比新加坡、美国教材对“份数定义”的处理，中国教材有较为明显的不足.新加坡、美国教材利用不同情境给出“份数定义”：“整体中的部分”、“组合里面的部分”再到“集合中的部分”，分成3个不同层次，逐步增加概念的抽象程度.这样做可使学生清晰感知分数“单位”的多种适当选择，有利于学生完整地、深入地理解“份数定义”.而中国教材“整体中的部分”的单一提法，易造成学生认识上的不足或错误理解[19].因此建议：份数定义的处理宜借鉴新加坡、美国教材的做法，对中国教材做出改进.

5.1.2 改进分数“商的定义”教材处理

分数的真正来源，在于自然数除法的推广.按照张奠宙先生的说法，分数“商的定义”体现了分数的本质，符合数系扩张的数学思想，理应成为分数引入、分数定义的首选的、核心的内容.三国教材尽管对“除法与分数”之间关系都用不少篇幅展开，但对其作用与意义突出不够.试想，若从“商的定义”入手引入分数，再到分割形成的“份数定义”，再到数轴上任意大小的分数，会否有助于去除当今教学中存在的对分数的种种认识不足（比如认为分数比1小，分数基本性质中对相等分数的错误认识），这样的顺序是否更有利于学生对分数概念的理解与建构？这值得思考.

5.1.3 加强分数“数线定义”的内容及教学

将分数在数线上直观表达出来，是促进学生正确理解分数定义的有力工具.它起到了将现实情境与具体操作物进一步转化为“数学符号”的作用，是沟通各种表征形式的良好介质，教材及教学理应重视其作用，增加分数“数线定义”的内容.在此，新加坡教材给了我们良好的启发：从“细长条形块”这一几何模型逐渐过渡到数学的语言与符号——数线，逐步抽象，更加符合学生的认知发展.

5.2 对教学实践的启示

长期以来中国教材及教学多采用“情境创设——提出问题——实物操作——‘图形’表征——定义、符号”的基本顺序，这种做法体现了数学与实际生活的联系.然而，数学本身的学科特征使其某种程度上具有脱离情境的特征，比如其几何解释、符号表达等.同时“现实情境”、“具体操作物”、“图形”等表征形式无一不为分数的“符号”表征及其认知服务.倘若一味强调上述顺序则易使教学陷入某种僵化模式，不利于学生对数学抽象本质的把握.需要处理好“数学与日常生活的联系”与“数学的形式特性”之间关系的辩证统一，既要突出知识的内在联系，又不过分强调情境学习[20].因此，结合内容特点，适度采用多元化的表征顺序，这方面新加坡教材、加州教材给予研究者重要启示.如，对分数定义，就不妨就从数学化的“商的定义”入手，以此为核心，联系分配、测量、比例等意义，逐步给出“份数定义”、“数线定义”及“比的定义”，则更有益于去除现今教学中学生易产生错误理解之处.为增强知识与实际生活的联系，可在学生真正掌握分数本质后，给出与实际生活联系密切的例子.再如，化假分数为带分数内容的处理，可适当简化，在分数除法定义的基础上，直接给出具体做法，而无需做多余的铺垫.总之，教学中宜视具体内容的不同而采取不同的表征顺序和处理方式.同时，多种不同的教学处理方式对学生思维发展的多维度、多向性亦是有益的.这是三国教材分数定义比较给予研究者的重要启示.

从教材比较的角度来看，文章仅对中、美、新三国教材对分数定义的处理进行了比对，对于分数内容，学生的学习困难不仅在定义，对分数的运算也存在很多问题，如对分数除法“颠倒相乘”的算理缺乏足够认识等，美、新两国是如何处理分数四则运算的？以及3套教材除却分数外的其它内容是否有可资借鉴的地方？另外，对于教材比较应采用的方法、针对不同内容应选择的合适切入点等都值得研究者深入、细致地分析、思考，以期通过合理、有效的方式比较、借鉴别国教材的成功做法，逐步改进中国的教材与教学.

[1]Paik J H.Fraction concepts: A Complex System of Mapping [D].Indiana University, ProQuest Information and Learning Company, 2005.

[2]巩子坤，杨玉东.错误仅仅是因为粗心吗[J].上海教育科研，2007，（9）：90-93.

[3]Kieren T E.On the Mathematical, Cognitive and Instructional Foundations of Rational Numbers [A].In: Lesh R A.Number and Measurement: Papers from a Research Workshop [C].Columbus, OH: ERIC/SMEAC, 1976.

[4]吕玉琴.分数概念文献探讨[J].台北师院学报，1991，（4）：573-605.

[5]Kieren T E.Rational and Fractional Numbers: From Quotient Fields to Recursive Understanding [A].In: Carpenter T P,Fennema E, Romberg T A.Rational Numbers: An Integration of Research [C].Hillsdale, NJ: Lawrence Erlbaum, 1993.

[6]Ministry of Education, Singapore.Singapore Tops the Trends in International Mthematics and Science Study (Timss)2003 [EB/OL].http://www.moe.gov.sg/media/press/2004/pr20041214.htm.

[7]卢江，杨刚.义务教育课程标准实验教科书小学数学三年级（上）[M].北京：人民教育出版社，2003.

[8]卢江，杨刚.义务教育课程标准实验教科书小学数学五年级（下）[M].北京：人民教育出版社，2005.

[9]卢江，杨刚.义务教育课程标准实验教科书小学数学六年级（下）[M].北京：人民教育出版社，2006.

[10]Teo S, Tiang K M.Discover Maths Textbook 2B [M].Singapore: Panpac Education Private Limited, 2007.

[11]Teo S, Tiang K M.Discover Maths Textbook 3B [M].Singapore: Panpac Education Private Limited, 2007.

[12]Shing L H.Discover Maths Textbook 4A [M].Singapore: Panpac Education Private Limited, 2007.

[13]Lai C C, Tan K L.Discover Maths Textbook 5A [M].Singapore: Panpac Education Private Limited, 2007.

[14]Lai C C, Tan K L.Discover Maths Textbook 6A [M].Singapore: Panpac Education Private Limited, 2009.

[15]Altieri M B.California Maths (Grade 2, 3, 4, 5) [M].Macmillan: McGraw-Hill, 2007.

[16]张奠宙.分数的定义[J].小学教学（数学版），2010，（01）：48-49.

[17]Lesh R, Post T, Behr M.Representations and Translations among Representations in Mathematics Learning and Problem Solving [A].In: Janiver C.Problems of Representations in the Teaching and Learning of Mathematics [M].Hilladale,NJ: Lawrence Erlbaum, 1987.

[18]Behr M J, Wachsmuth I, Post T R, et al.Order and Equivalence of Rational Numbers: A Clinical Teaching Experiment[J].Journal for Research in Mathematics Education, 1984, (15): 323-341.

[19]张奠宙.“分数”教学中需要澄清的几个数学问题[J].小学教学（数学版），2010，（1）：4-6.

[20]郑毓信.数学教育哲学的理论与实践[M].南宁：广西教育出版社，2008.