儒歇定理的推论、推广及应用

张 庆

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

儒歇（Rouche）定理是复变函数论中的一个著名定理，在理论和应用上都有着极其重要的地位。利用儒歇定理可以考察函数零点的个数及其分布情况。本文主要探讨应用儒歇定理给出复变函数零点的个数及分布情况的方法以及儒歇定理的等价形式和推广形式。

1 预备知识

引理1（辐角原理）[1]设C是一条围线，若函数 f(z)满足以下条件：

（1）f(z)在C的内部是亚纯的（即除可能有极点外解析）；

（2）f(z)在C上解析且不为零；则有

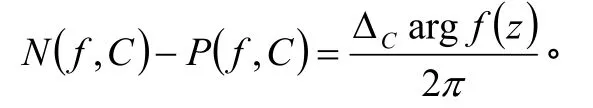
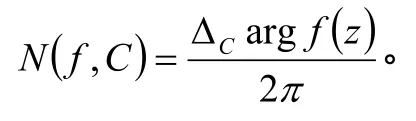
注：条件（2）减弱为“f(z)连续到边界C，且沿C有f(z)≠0”，则辐角原理的结论仍然成立。

引理 2（经典儒歇（Rouche）定理）[2]设C是一条围线，函数f(z)及φ(z)满足以下条件：

（1）f(z)及φ(z)在C内部均解析，且连续到C；

那么，

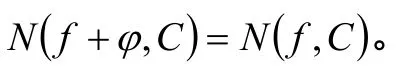
2 儒歇定理的推论与推广

定理1设C是一条围线，函数f(z)及g(z)满足：

（1）f(z)及g(z)在C的内部均解析，且连续到C；

则

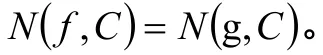
证明 因为f(z)及g(z)在C的内部均解析，所以

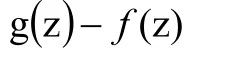
在C内解析，设

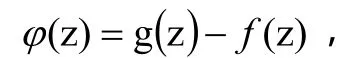
则由条件（2），在C上

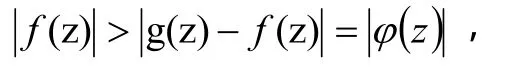
由引理2，

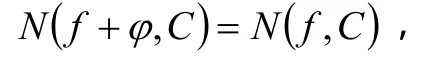
又

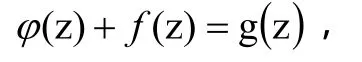
因此

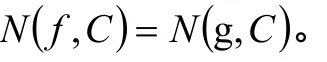
容易证明经典的儒歇定理与上述定理1是等价的。

由儒歇定理可以得到如下推论：

（1）f(z)、φ(z)和ψ(z)在C的内部均解析，且连续到C；

那么，

证明 由引理2有：

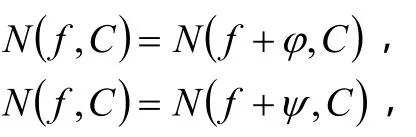
所以，

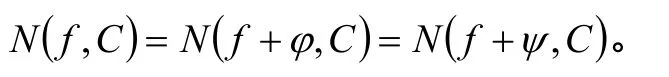
在这个推论中条件（2）可以换成：在C上

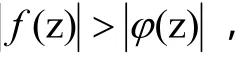
且

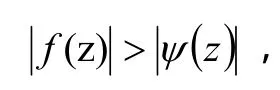
则结论仍然成立。

如果把经典的儒歇定理的条件适当放宽，即将条件（1）放宽为“函数f(z)及φ(z)在C的内部亚纯，且连续到C”其余条件不变，结论将相应得到改变，这将得到经典的儒歇定理的一个推广。

定理 2（儒歇定理的推广）设C是一条围线，函数f(z)及φ(z)满足以下条件：

（1）f(z)及φ(z)在C内部亚纯，且连续到C；

那么，

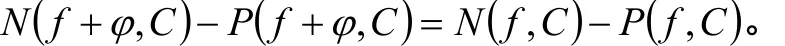
证明 由条件（2）知，在C上，

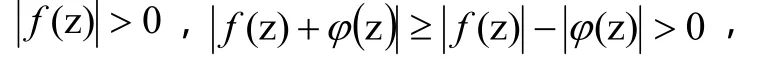
由引理1（辐角原理），有：

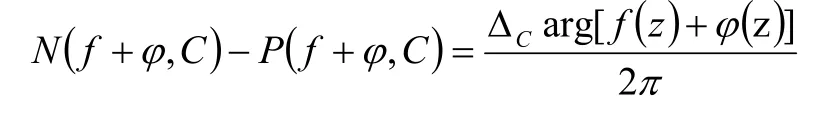
及

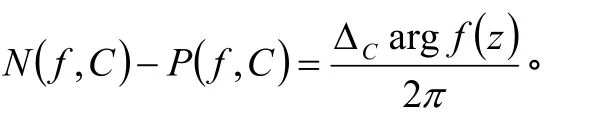
只需证明

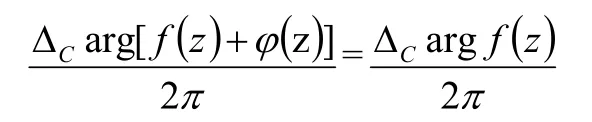
成立。因为

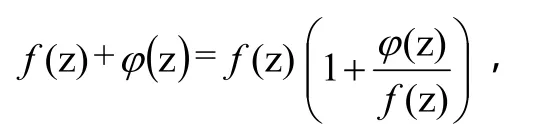
所以

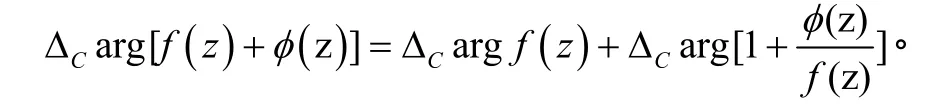
令

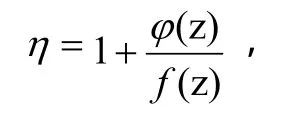
由条件（2），在C上

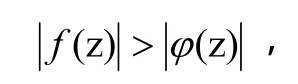
所以

所以

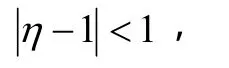
从而

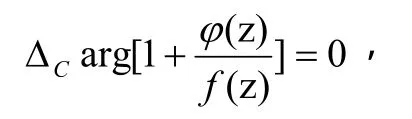
因此结论成立。

3 儒歇定理的应用

3.1 证明代数学基本定理

代数学基本定理：任何一个n次多项式

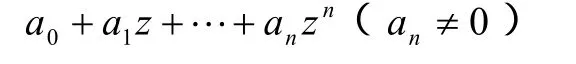
在复数域中有且只有n个根（重根按重数计）。

该定理是代数学的基石，但用纯粹的代数方法证明却十分困难且繁杂，因此在高等代数教材中一般未给出它的证明；然而，利用儒歇定理却可以给出简洁的证明。

证明 设

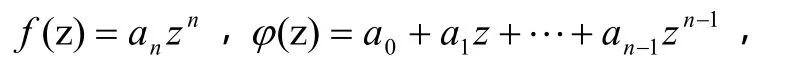
取

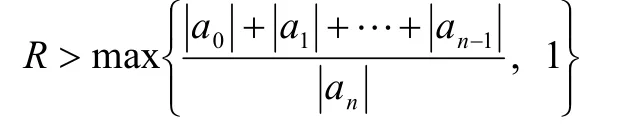
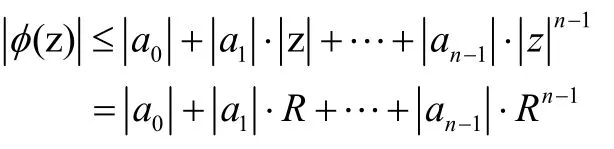
又

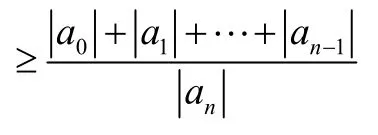
所以

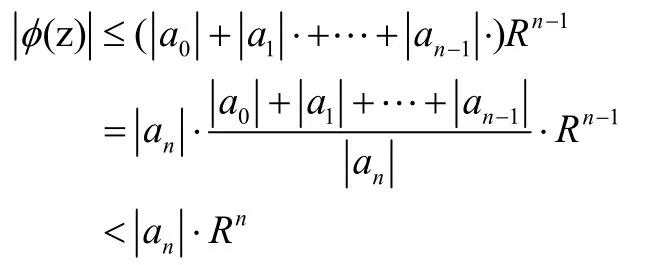
因此，在圆周C上，

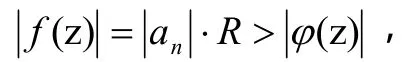
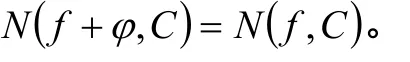
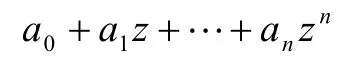
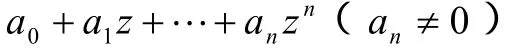
事实上，任取 z0在上或其外部，则

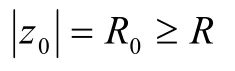
于是，

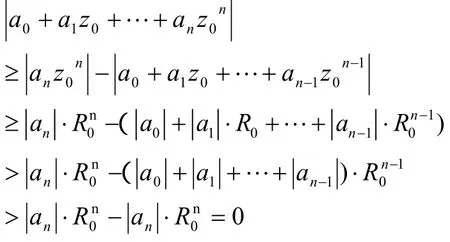
即z0不是n次多项式

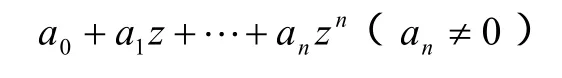
的根。

综上，n次多项式

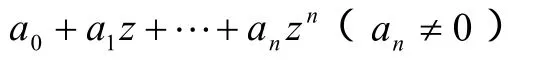
在复数域中有且只有n个根。

3.2 确定在一定范围内函数的零点个数

确定n次多项式函数满足一定条件的零点的个数以及零点出现在什么范围是复变函数论研究的重点理论问题，利用儒歇定理可以很容易解决此类问题。

例1 设n次多项式

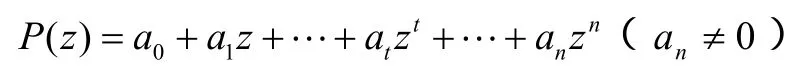
并且

则

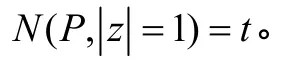
证明 设

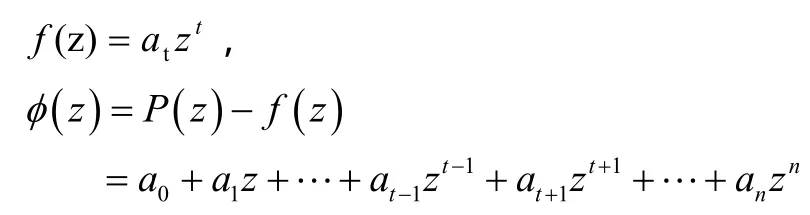
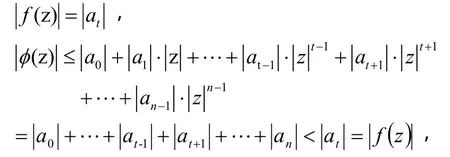
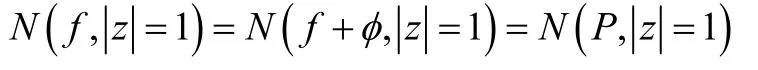
而

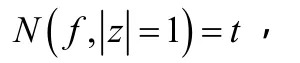
所以，

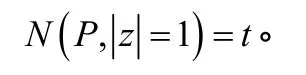
注：进一步利用例1的结论，可以确定多项式函数何处有零点，何处无零点。

除了关注多项式函数零点的研究，在此基础上我们还关注多项式函数与某些基本初等解析函数的和得到的解析函数的零点问题的讨论。

证明 设

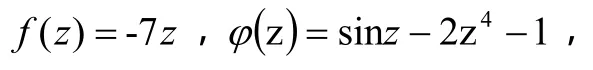
由儒歇定理，

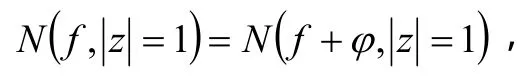
而

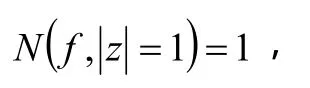
所以，

即

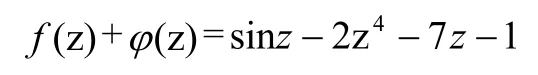
例3 证明：函数

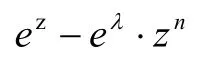
证明 设

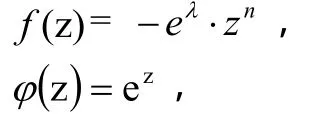
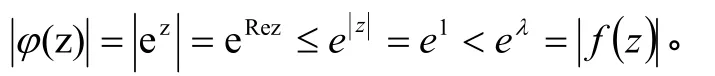
由儒歇定理，

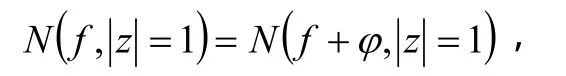
而

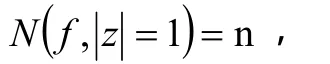
所以，

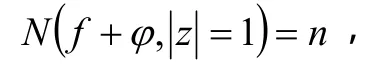
即

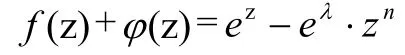
3.3 证明零点定理

证明 若f(0)=0，则f(z)至少有一个零点0。

由儒歇定理，

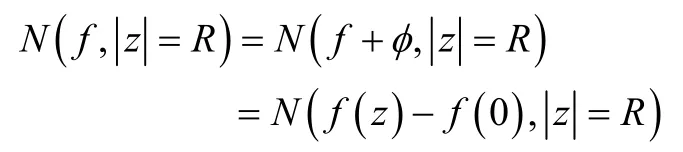
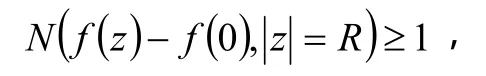
从而，

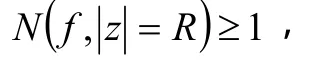
3.4 证明不动点存在问题

如果z(z)=f，则称z是 f(z)的一个不动点。

证明 取

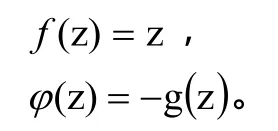
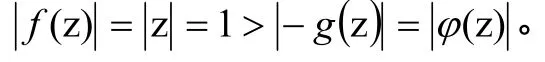
由儒歇定理

即存在z0，且，使

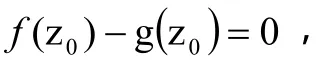
3.5 证明赫尔维茨（Hurwitz）定理

赫尔维茨定理[3]如果

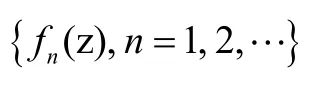
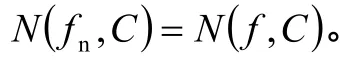
证明 由已知及魏尔斯特拉斯定理[5]易知，f(z)在D内解析，且设

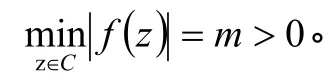
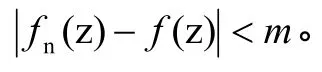
所以，在C上，当Nn＞时，

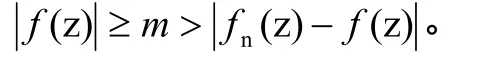
由定理1，得

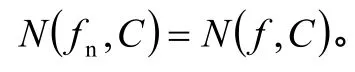
以上给出了儒歇定理在五个方面的应用，至于儒歇定理的推广的应用可参阅文献[4]。

[1] 钟玉泉.复变函数论(第三版)[M].北京:高等教育出版社,2003:262.

[2] 余家荣复变函数[M].北京:人民教育出版社,1980:128.

[3] 钟玉泉.复变函数学习指导书[M].北京:高等教育出版社,1996:326.

[4] 钟玉泉.一个解析函数定理的推广[J].四川大学学报(自然科学版),1990(1):86-87.

[5] 钟玉泉.复变函数论(第三版)[M].北京:高等教育出版社,2003:153.