电特大目标散射特性研究中的快速多极子技术

胡明春

(南京电子技术研究所， 南京210039)

0 引言

电特大目标散射特性的求解是从雷达探测、目标特性及射频隐身设计等实际工程中提炼出的一个颇具挑战性的科学问题。所谓电特大目标，是指目标的电尺寸(几何尺寸折算为入射波波长个数)达到数百甚至上千。这类问题的求解的传统方法是高频近似方法［1-4］。高频近似法具有计算资源消耗小、算法简单、求解速度快甚至可以实现“实时”求解等优势，其中最为典型的是美国DEMACO公司基于高频近似法开发的XPATCH软件［5］，该软件在美国军工行业发挥了重大的作用。然而高频近似法本质上是标量波方程典型解的应用，难以准确地描述三维电磁散射中复杂的电磁矢量关系，精度缺乏保证，只适于目标散射特性的粗略估计。在实际的雷达工程应用中，大多数目标在雷达工作波段既表现出宏观的电大尺寸，又不可避免地具有细节上的复杂结构，要精确获得此类目标的散射特性，就必须采用全波数值方法而非高频近似法。

全波数值法可分为时域有限差分法、有限元法和矩量法三种基本类型［6］，其中时域有限差分法及有限元法均需要对三维目标体进行单元划分，且需设置边界条件以缩小求解区域范围，因而未知量比较多;而矩量法只需要对三维目标的表面进行离散，且无须像微分方程法那样必须设置边界条件，具有求解区域小和未知量少的优点，因此全波数值方法中最适合散射问题求解的是矩量法。矩量法是由Harrington R.F.等人于20世纪60年代提出的一种离散电磁场积分方程的数值方法［7］，Rao等人提出RWG基函数来拟合任意物体表面的电流［8］，促进了该算法在电磁特性精确计算中的应用。此后，矩量法在理论上和实际应用中都取得了巨大的进步，广泛应用于各种天线辐射、复杂散射体散射以及静态或准静态等问题的求解。矩量法的显著特点是精度高，其本质在于矩量法所离散的是积分方程，矩阵元素之间的相互作用通过格林函数准确描述，正因为如此，由于矩量法产生的矩阵是满阵，对应的存储量为O(N2)。若用矩阵求逆的方法求解，其算法复杂度达到O(N3)，即使用迭代法求解，每次迭代的算法复杂度O(N2)。因此，对于未知量较多的问题，计算资源很难满足要求，这也是传统矩量法发展数十年后所能求解问题的规模仅限于几个波长，无法实现电特大目标散射特性的精确求解的根本原因。

矩量法精确但无法求解电大目标散射特性的尴尬局面直到快速多极子技术的出现才得以结束。快速多极子技术是一项基于矩量法的算法加速技术，可以大大降低内存及算法复杂度——快速多极子技术使得传统矩量法的O(N2)降低到O(N1.5)，多层快速多极子技术可以进一步将内存及算法复杂度降至O(NlgN)甚至O(N)，并行技术的出现进一步提升了快速多极子技术的加速性能。快速多极子技术的关于该算法的原理将在第1节继续阐释。

本文围绕快速多极子技术这一电特大目标散射计算的关键技术展开，后续的安排如下:第1节介绍了快速多极子技术的加速原理及发展历程，第2节通过电特大目标散射特性计算的典型案例展示算法的求解能力，第3节展望了多极子技术的发展趋势，第4节给出总结。

1 快速多极子技术的原理及发展历程

快速多极子算法的基本数学原理在20世纪90年代初由Rokhlin V.在文献中提出［9］，其核心是通过加法定理将格林函数展开成球谐函数的级数表达式。基于此数学原理，Rokhlin、Engheta及 Lu C.C.和 Chew W.C.等人很快将此算法应用于目标的电磁散射特性计算［9-12］。下面简要地给出快速多极子技术与电磁散射特性求解相结合的数学推导。

三维导体目标的电磁散射问题可用电场积分表示为

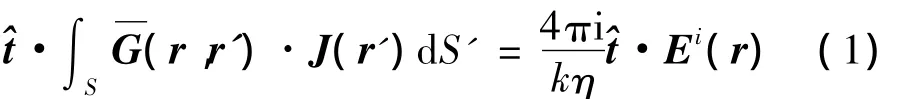
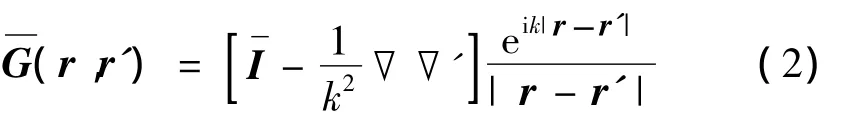
式中:r为目标表面S上场点对应的矢径;^t为S上场点对应的单位切向矢量;Ei为入射激励场;R=|r-r'|。式(2)利用加法定理展开并表示为角谱空间积分为

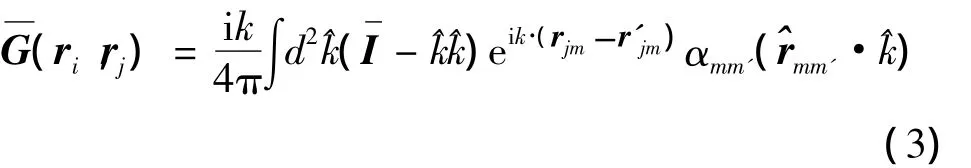
其中

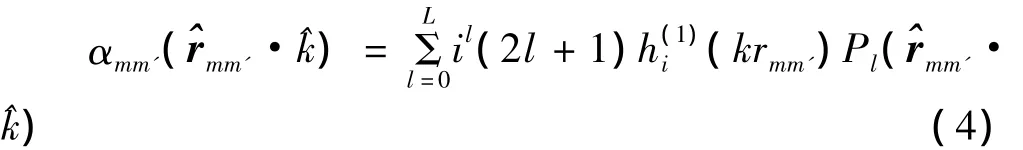
式中:h(1)i和Pi分别表示第一类球汉克尔函数和勒让德函数;∫d2^k表示角谱空间单位球面上的积分。式(3)中可以通过合理选取高斯积分点进行精确计算，这样就得到了离散式(1)的两种方法。在快速多极子算法中，将所有的基函数(每个未知量对应一个基函数)根据几何位置分若干组。对于相邻组(极少数)，用式(1)直接计算矩阵元素;对于其余的非相邻组(绝大多数)，则将式(3)代入式(1)表示基函数之间为远场相互作用。该算法原理也可从物理角度解释，即快速多极子方法的将目标表面离散得到的各个电流作用看成是一个一个的子散射体，通过分组将子散射体之间的作用分为近场组作用和远场组作用。通常最细层组的电尺寸不低于0.2。当两个非空组之间至少有一个公共点时，两个组之间的关系属于近场组，使用矩量法直接计算两个组内基函数之间的互作用。当两个非空组之间至少相隔一个组时，它们之间的关系属于远场组，采用快速多极子方法聚集-转移-发散来计算。对于源点组来说，该组中心代表了组内所有子散射体对其相邻组之间的作用;对场点组来说该组中心代表了来自该组的所有非相邻组对它的作用。通过这种分组的方式，减少了基函数之间作用的次数来降低计算复杂度和内存需求。电流之间互耦作用的次数由原来矩量法的O(N2)降低到O(N1.5)。

单纯的快速多极子技术在未知量较大时仍然需要较多的计算资源，为了进一步提高算法的加速性能，美国依利诺依大学Chew W.C.教授在快速多极子方法的基础上提出了多层快速多极子方法(多层快速多极子方法是快速多极子方法的推广)［13-15］。多层快速多极子方法是基于树形结构的计算，其特点是逐层聚集、逐层转移、逐层发散、嵌套递推。对于二维情况，它将求解区域用一正方形包围，然后再细分为4个子正方形，该层记为第一层。将每个子正方形再细分为4个更小的子正方形，则得到第二层，此时共有42个正方形。依次类推得到更高层。对于三维情况，则用一正方体包围记为0层，经过一次细分后得到8个子正方体记为第1层。依次类推细分下去，直到子正方体的边长为0.2左右，由此可以确定多层快速多极子方法在求解一个给定电尺寸的目标散射时所需的层数。该方法的出现使得矩量法求解的算法复杂度由O(N1.5)向O(NlgN)迈进，散射问题的求解规模由数十个电波长拓展至数百个电波长。

在快速多极子算法不断演进的同时，Chew W.C.教授课题组进一步将算法与超级计算机的并行处理结合起来，率先开展了多层快速多极子并行算法的研究［16-19］，国内相关课题组也迅速跟进并取得了突出的成果［20-23］。需要注意的是，多层快速多极子并行算法与串行算法有根本不同，其开发并非只是在原有串行算法上的简单调整，而要从算法原理到数据结构等方面做出根本改变，才能实现高效的并行算法，其中负载均衡和转移矩阵是并行化的难点。目前，利用并行多层快速多极子技术已实现数百个核并行运算，散射问题的求解规模达到上千个电波长。

2 快速多极子技术在电特大目标散射特性求解中的应用

近几年，国内外多个团队在快速多极子技术(尤其是并行多层快速多极子技术)方面取得了重大进展［24-33］，完成了一系列典型电特大目标散射特性求解算例。下面将这些算例中的电特大目标分为标准体、民用目标及军用目标三类，结合典型算例来介绍快速多极子技术在电特大目标散射特研究中的求解能力。

2.1 标准体的散射特性求解

下面展示的是理想导体球散射特性研究算例。之所以选择球体算例，是因为导体球的RCS有解析解，便于验证算法的精度。图1是土耳其Levent Gurel课题组利用并行多层快速多极子技术完成的半径为340个电波长的金属球雷达散射截面(RCS)算例［32］。该算例对应的未知量个数为540 659 712，采用了64个Intel Xeon Nehalem-Ex L755处理器并行处理。由图1c)可见，基于快速多极子技术的矩量法所得RCS与解析解吻合，验证了算法的精度。

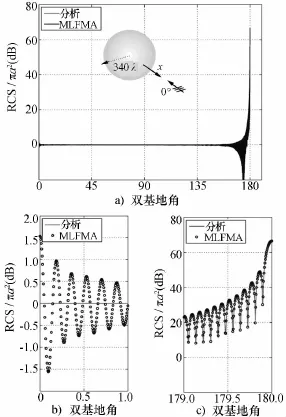
图1 金属球的散射(半径340个电波长)

北京理工大学盛新庆教授课题组于2011年报道了一个直径为1 000个波长的金属球，采用512 778 700个未知数，计算结果如图2所示。显然，采用并行多层快速多极子技术的计算结果与解析解吻合，再次验证了算法的精度，也展示了国内在快速多极子技术研究方面的实力。

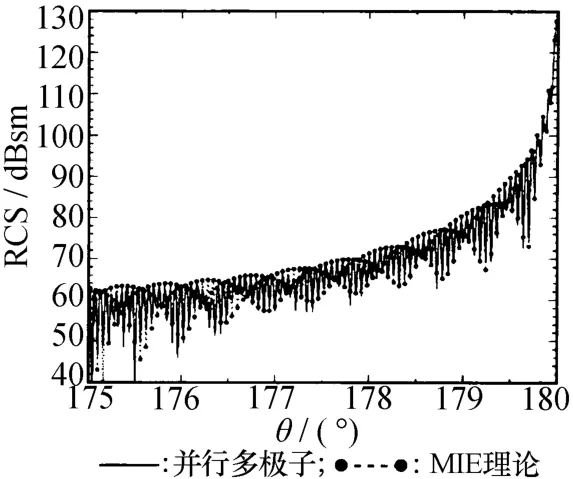
图2 金属球的散射(半径500个电波长)

近期，国际上较为轰动的一个算例是西班牙的Jose Manuel Taboada团队近期完成的一个最新Almond的散射特性求解算例［33］，Almond是美国 NASA发布的用于校验散射特性求解算法的标准体。该算例中入射波的频率设定为3 THz，对应的最大几何尺度的电尺寸为2 524个电波长，对应1 042 977 546个未知量。该算例在“Finis Terrae”超级计算机上完成，用了64个节点(每个节点含16个核，共计1 024个处理器)，消耗了5 TB内存，这是国际上公开报道突破10亿未知量的算例，展示了快速多极子技术的强大求解能力，是一个新的里程碑。

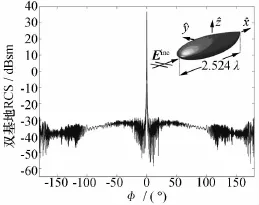
图3 金属Almond算例

2.2 介质体目标散射特性求解

在电磁计算中，求解介质体散射特性的方程与理想导体不一样，方程的迭代收敛速度不一样，对应的求解技术也不一样。目前，多层快速多极子技术已开始在导体目标的散射特性求解中应用［32］。图4所示的是均匀介质体半球的散射特性仿真结果(介质半球的半径为25 mm，相对介电常数为4.8)，平面入射波频率为960 GHz，求解中用了39 389 184个未知量。

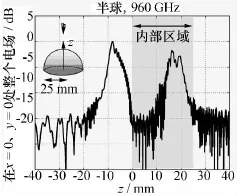
图4 均匀介质半球算例

图5给出的是多层介质体板算例(介质板边长为2 cm、高 0.41 cm、相对介电常数为 1.6)，平面入射波频率为960 GHz，该算例用了39 628 800个未知量。

2.3 民用目标的散射特性求解

除了在在标准体散射研究中的应用，快速多极子技术还用在汽车散射特性这类复杂民用目标的散射特性研究中。图6展示了基于快速多极子技术加速的散射求解技术用于汽车散射特性研究的结果。在该算例中，车厂为3.49 m，入射波频率为79 GHz，采用了620 739 632个未知数个基函数来表示车身的等效电流。

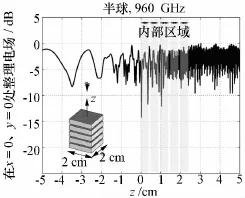
图5 多层介质体板的散射

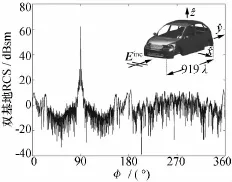
图6 汽车的散射

2.4 军事目标的散射特性求解

目前，基于快速多极子技术的散射特性精确求解技术广泛应用于军事目标的散射特性求解。图7为北京理工大学盛新庆教授课题组于2008年完成的飞机RCS算例［20］，对应最大几何尺度的电尺寸超过2 000个电波长，采用289 344 192个未知数来模拟飞机模型。此算例采用并行多层快速多多极子技术，将计算区域分为14层，在中科院“深腾”高性能计算平台上采用64个处理器并行处理，总计消耗814 GB内存。图8为该团队2011年完成的舰船模型散射特性研究算例，该算例中军舰长度为2 144个电波长，采用3亿多个未知数完成舰体的模拟。

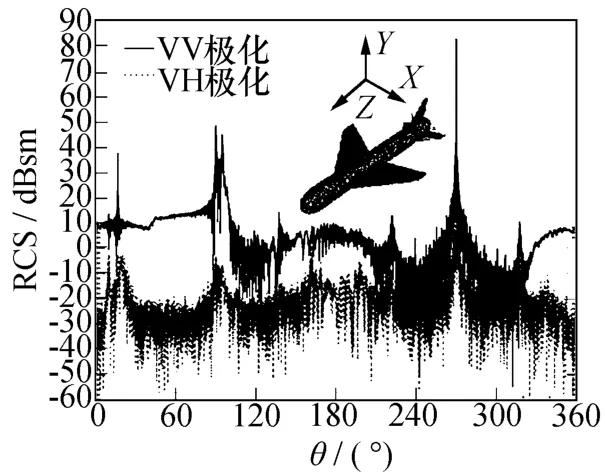
图7 A-2000飞机模型RCS仿真算法

图9为西班牙的Jose Manuel Taboada团队完成的一个隐身飞机模型的散射特性求解算例。频率为820 GHz的平面波从机头前方斜30°入射，该算例中用到的未知数高达538 967 040。

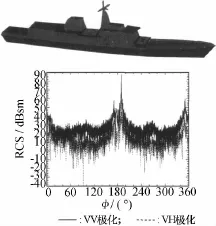
图8 舰船的散射

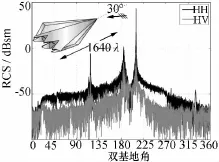
图9 隐身飞机模型的散射

3 快速多极子技术发展展望

快速多极子的数学原理提出来已有二十多年，在快速多极子加速技术的推动下，可精确求解目标电磁散射特性的全波数值法求解规模和求解能力实现了质的飞跃。目前，快速多极子技术已从最初的单层发展为多层，并结合超级计算机发展为并行多层快速多极子技术，快速多极子技术的理论和算法框架日臻完善。当前，快速多极子技术的发展更多地体现为并行算法与超级计算机上的深度优化与快速多极子技术的应用范畴的拓展。

在与超级计算机结合方面，快速多极子技术的发展的趋势是结合超级计算机的体系构架、硬件结构进一步提升算法的并行能力(如考虑OpenMP及MPI的算法特性，对超级计算机节点之间及各个节点内部采用不同的并行化策略;考虑各个节点之间通信开销及负载均衡等)，实现更大规模的并行求解。

目前，快速多极子技术的应用范畴方面越来越广泛，一个典型的例子是快速多极子技术用于“合元极”技术［15］，在该技术特别适合于带涂覆层的合理想导体目标的电磁散射特性研究。此外，多个课题组对快速多极子技术在均匀介质体等不同类型目标的散射特性开展研究等。

4 结束语

电特大目标散射特性的精确求解既是重要的科学问题，又在雷达工程应用等领域有着迫切的应用需求，全波数值法是较好的求解途径。在全波数值法中，又以矩量法最为适合。在早期，传统矩量法的求解规模严重受限于算法复杂度及内存需求，无法实现电大目标散射特性求解;在20世纪末，快速多极子技术的出现结束了矩量法不能求解大规模电磁散射问题的尴尬局面，这项革命性的加速技术极大地降低了矩量法精确求解的算法复杂度和内存需求，使得全波数值法实现电特大目标的散射特性成为可能;目前，随着快速多极子技术(尤其是并行多层快速多极子技术)的日臻成熟，精确算法求解电磁散射问题的规模可达到电尺寸为数千个电波长，未知量为10亿以上，达到了空前的求解能力。

［1］Youssef N N.Radar cross section of complex targets［J］.Proceedings of the IEEE，1989，77(5):722-734.

［2］Rius J M，Ferrando M，Jofre L.High-frequency RCS of complex radar targets in real-time［J］.IEEE Transactions on Antennas and Propagation，1993，41(9):1308-1319.

［3］Andersh D J，Hazlett M，Lee S W，et al.XPATCH:A high-frequency electromagnetic scattering prediction code and environment for complex three dimensional objects［J］.IEEE Antennas and Propagation Magazine，1994，36(1):65-69.

［4］Rius J M，Ferrando M，Jofre L.GRECO:graphical electromagnetic computing for RCS predietion in real time［J］.IEEE Antennas and Propagation Magazine，1993，35(2):7-17.

［5］Lee S W，Reeves D D，Sullivan D P，et al.XPATCH:a high-frequency electromagnetic scattering code and environment for complex three-dimensional objects［J］.IEEE Antennas and Propagation Magazine，1994，36(1):65-69.

［6］盛新庆.计算电磁学要论［M］.北京:科学出版社，2004.Sheng Xinqing.A brief treatise on computational electromagnetics［M］.Beijing:Science Press，2004.

［7］Harrington R F.Field computation by moment methods［M］.Malabar，Florida:Krieger Publishing Company，1983.

［8］Rao S M，Wilton D，Glisson A W.Electromagnetic scattering by surfaces of arbitrary shape［J］.IEEE Transactions on Antennas and Propagation，1982，30(3):409-418.

［9］Rokhlin V.Rapid solution of integral equation of scattering theory of two dimensions［J］.Journal of Computational Physics，1990，36(2):414-439.

［10］Coifman R，Rokhlin V，Wanzura S.The fast multipole method for the wave equation:A pedestrian prescription.IEEE Antennas and Propagation Magazine，1993，35(3):7-12.

［11］Engheta N，Murphy W D.The fast multipole method for electromagnetic scattering problems［J］.IEEE Transactions on Antennas and Propagation，1992，40(6):634-641.

［12］Lu C C，Chew W C.A multilevel algorithm for solving boundary-value scattering［J］.Microwave Optical Technology Letters，1994，7(10):466-470.

［13］Song J M，Chew W C.Multilevel fast multipole algorithm for solving combined field integral equations of electromagnetic scattering［J］.Microwave Optical Technology Letters，1995(10):14–19.

［14］Song J M，Lu C C，Chew W C.MLFMA for electromagnetic scattering by large complex objects［J］.IEEE Transactions on Antennas and Propagation，1997，45(10):1488-1493.

［15］Sheng X Q，Jin J M，Song J M，et al.Solution of combined-field integral equation using multilevel fast multipole algorithm for scattering by homogeneous bodies［J］.IEEE Transactions on Antennas and Propagation，1998，46(11):1718-1726.

［16］聂在平，胡 俊，姚海英，等.用于复杂目标三维矢量散射分析的快速多极子方法［J］.电子学报，1999，27(6):104-109.Nie Zaiping，Hu Jun，Yao Haiying，et al.The fast multipole methods for vetor analysis of scattering from 3-dimensional objects with complex structure［J］.Acta Electronica Sinica，1999，27(6):104-109.

［17］Velamparambil S，Song J M，Chew W C，et al.ScaleME:a portable scaleable multipole engine for electromagnetic and acoustic integral equation solvers［C］//Internationl Symposium on IEEE Antennas and Propagation.［S.l.］:IEEE Press，1998(3):1774-1777.

［18］Velamparambil S，Chew W C，Song J M.10 million unknowns:is it that big［J］.IEEE Transactions on Antennas and Propagation，2003，45(3):43-58.

［19］Velamparambil S，Chew W C.Analysis and performance of a distributed memory multilevel fast multipole algorithm［J］.IEEE Transactions on Antennas and Propagation，2005，53(8):2719-2727.

［20］潘小敏，盛新庆.一种多层快速多极子的高效并行方案［J］.电子学报，2007，35(3):88-93.Pan Xiaomin，Sheng Xinqing.A highly efficient parallel approach of multi-level fast multipole algorithm［J］.Acta Electronica Sinica，2007，35(3):567-571.

［21］卢光辉，孙世新，聂在平，等.并行处理技术在电大尺寸复杂目标电磁散射中的应用［J］.电子学报，2003，31(6):882-885.Lu Guanghui，Sun Shixin，Nie Zaiping，et al.Applicaiton of the parallel processing techology to electromagnetic scattering from electrically large complex objects［J］.Acta Electronica Sinica，2003，31(6):882-885.

［22］Rui P L，Chen R S.A spectral multigrid method combined with MLFMA for solving electromagnetic wave scattering problems［J］.IEEE Transactions on Antennas and Propagation，2007，55(9):2571-2577.

［23］Pan X M，Sheng X X Q.A sophisticated parallel MLFMA for scattering by extremely large targets［J］.IEEE Transactions on Antennas Propagation，2008，50(3):129-138.

［24］Gurel L，Ergul O.Fast and accurate solutions of extremely large integral-equation problems discretised with tens of millions of unknowns［J］.Electronics Letters，2007，43(9):499-500.

［25］Ergul O，Gurel L.Parallel-MLFMA solution of CFIE discretized with tens of millions of unknowns［C］//The Second European Conference on Antennas and Propagation.Edinburgh:IEEE Press，2007.

［26］Ergul O，Gurel L.Efficient parallelization of the multilevel fast multipole algorithm for the solution of large-scale scattering problems［J］.IEEE Transactions on Antennas and Propagation，2008，56(8):2335-2345.

［27］Ergul O，Gurel L.A hierarchical partitioning strategy for an efficient parallelization of the multilevel fast multipole algorithm［J］.IEEE Transactions on Antennas and Propagation，2009，57(6):1740-1750.

［28］Taboada J M，Landesa L，Obelleiro F，et al.High scalability FMM-FFT electromagnetic solver for supercomputer systems.IEEE Transactions on Antennas and Propagation，2009，51(6):20-28.

［29］Taboada J M，Araujo M，Bertolo J M，et al.MLFMA-FFT parallel algorithm for the solution of large-scale problems in electromagnetic［J］.Progress in Electromagnetics Research，2010，105:15-30.

［30］Pan X M，Pi W C，Sheng X Q.On openmp parallelization of the multilevel fast multipole algorithm［J］.Progress in Electromagnetics Research，2011，112:199-213.

［31］Ergul O，Gurel L.Rigorous solutions of electromagnetic problems involving hundreds of millions of unknowns.IEEE Transactions on Antennas and Propagation，2011，53(1):18-27.

［32］Ergul O，Gurel L.Accurate solutions of extremely large integral-equation problems in computational electromagnetics［J］.Proceedings of the IEEE，2013，101(2):342-349.

［33］Taboada J M，Araujo M G，Basteiro F O，et al.MLFMAFFT parallel algorithm for the solution of extremely large problems in electromagnetics［J］.Proceedings of the IEEE，2013，101(2):350-363.