基于Tribon M3平台的电缆贯穿件快速定位方法研究

程凌云，廖洪泉，严晨刚，潘江鸿

（上海船厂船舶有限公司，上海 202146）

0 引 言

受国际金融危机的影响，航运贸易额缩减，持续的“接单难”、“交船难”使船舶市场的竞争更加激烈。由此，对船舶产品设计工作提出了更高的要求，产品的设计周期越来越短，设计精度越来越高，设计深度也越来越深。为适应当前复杂环境下的船舶市场要求，经过实践论证，国内多家骨干船厂在引进 AVEVA公司Tribon三维建模软件的基础上进行必要的二次开发，形成适合各自船舶制造特点的CAD/CAM系统。本文结合28000t多用途船的设计，论述了基于Tribon三维建模软件的贯穿件精准定位方法，为今后船舶设计以及船舶软件的开发提供参考。

1 电缆贯穿件常规定位方式

1.1 水平甲板下贯穿件定位

在Tribon M3中，对于每个电缆贯穿件都有一个如图1所示重心点 P( X,Y,Z)。

在模型新建完后，该点就自动生成。对于电气施工生产而言，1H的值是定位电缆贯穿件必不可少的，如果贯穿件所处位置的顶部甲板为水平甲板，则从图1中可以得出：

其中贯穿件的重心点 P( X,Y,Z)是已知的，对于水平甲板，其距离基线的高度是固定的，即图1中H值是已知的，因此很快就可以得出贯穿件距离顶部甲板的定位尺寸 H1。

1.2 倾斜甲板下贯穿件定位

1.1中叙述的方法仅对处于水平甲板下的贯穿件的定位有效，对处于倾斜甲板下的贯穿件，1.1中的计算方式就不适用了。从图2中可以得出倾斜甲板下贯穿件的定位尺寸为：由于甲板发生了倾斜，所以甲板距离基线的高度H不是固定不变的。

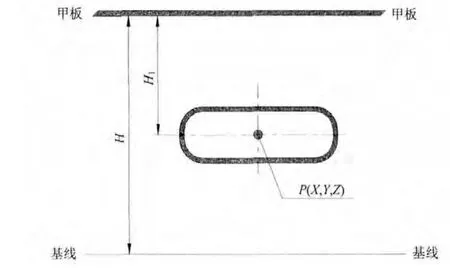
图1 水平甲板下贯穿件定位

图2 倾斜甲板下贯穿件定位

要得到 H1的值，就必须得到贯穿件的重心点正上方 P1点的Z轴坐标 Z1，且 Z1值是随甲板变化而连续变化的。为了得出 Z1的值，常用差值补偿方法计算，如图3中所示，已知倾斜甲板的最高点 A ( XH,YH,ZH)，和最低点 D ( XL,YL,ZL)坐标，从图3中可以得出：

图3 倾斜甲板下常规定位方式

若甲板向X方向倾斜，则可以推出B、C点坐标分别为： B( XH,YL,ZL),C(X,YL,ZL)，由此可以得出：

将以上算式合并后得出贯穿件的定位高度为：

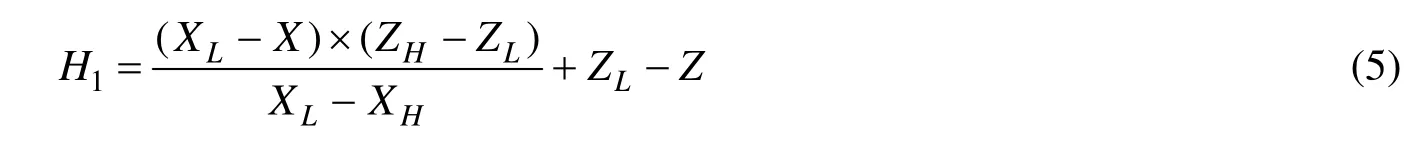
利用差值补偿方法计算出的贯穿件定位尺寸虽然较为准确，但有很大的局限性；首先这种方法对甲板倾斜方向的依赖性很大，遇到倾斜方向不明确或者不规则的甲板时，这种方法将面临大量的空间距离转换运算；其次该方法具有很强的针对性，不利于同类型船舶引用。

2 基于数学模型的贯穿件定位方法

2.1 平面甲板数学模型

在Tribon M3中，每个船舶模型都有一个三维坐标系，坐标系原点位于基线上 0FR= 、 0CL= 的位置，以船艏方向为X轴正向，以左舷方向为Y轴正向，以基线往上且垂直于X、Y轴的方向为Z轴正向。船体模型是由坐标系中多个平面、曲面甲板或舱壁等构件组成的组合体，因此将这些甲板或舱壁作为坐标系中的平面或曲面，运用平面方程和曲面方程将整个船体模型抽象成一组由多个方程式组成的数学模型。以图4中的倾斜甲板为例：令倾斜甲板为平面A，设经过点 ( x0,y0,z0)平面A的方程为[1]：

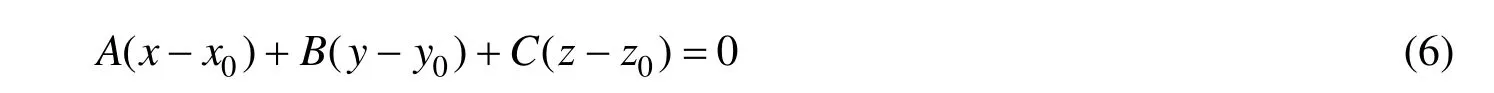
在平面A上任取不在同一直线上的三个点 PH(XH,YH,ZH)、PC(XC,YC,ZC)、PL(XL,YL,ZL)，利用三点坐标求出平面A的法向量[2]：

解式（7）可得：

将上述 A , B, C及 PH(XH,YH,ZH)、PC(XC,YC,ZC)、PL(XL,YL,ZL)中任意一点，代入平面A的方程式中即可得出平面的一般方程[1]：

求出倾斜甲板在船体坐标系中的平面方程式后，对处于该倾斜甲板下任意位置的贯穿件，已知其重心点P(X,Y,Z)，则其定位尺寸为：

因为1P点位于平面A上，所以：

因此贯穿件距离顶部的尺寸为：

图4 倾斜甲板下数学模型定位方式

式中A、B、C、D的值上面方程已经求出，从图4中可知 P1(X1,Y1,Z1)点和 P(X,Y,Z)点具有相同的X、Y坐标，而 P(X,Y,Z)点为贯穿件的重心点，是已知点。故贯穿件的定位高度为：

2.2 不规则倾斜甲板数学模型

在船体模型中，有些甲板并非连续倾斜甲板，例如船舶的主甲板面，其成拱形状，且甲板中间为水平甲板，只有两侧为倾斜甲板，如图5所示。

对于这种倾斜不连续的甲板面，可将其划分为多个平面，并对每个平面设定边界以区分。如可将图5划分为3个区域：45P P（倾斜）、56P P（水平）、67P P（倾斜），为每个区域划定边界：

按照2.1中所述的方法对每个区域的平面求其方程式，即得到主甲板面的数学模型：

图5 不规则倾斜甲板下数学模型定位方式

根据边界条件判断后，就能计算出贯穿件的定位尺寸：

同样对于其他处于任意位置向任意方向倾斜的平面，只要得到该平面的边界条件，就能将该平面转换成对应的数学模型。这样就能将全船的甲板面都转换成数学模型，组成了一个由数学模型构成的甲板层高定义系统，对处于船体结构上任意位置的贯穿件，都能准确给出其与顶部甲板的距离。

2.3 计算机辅助实现数学模型

2.3.1 计算机辅助模型的结构分析

在2.1和2.2中确定了船舶甲板的数学模型后，为了快速计算贯穿件定位尺寸，需要借助计算机程序建立一个标准的船舶甲板数学模型库。该模型库包含三个部分：标准方程、边界定义以及甲板模型初始化数据（如图6所示）。“标准方程”包含各种平面和曲面的通用标准方程以及这些方程的索引，“边界定义”用于定义各个甲板模型的边界以确定模型的有效区域，“甲板模型初始化数据”用于储存指定甲板的特征信息，用于甲板模型所对应的方程式的初始化。通过将指定船舶的甲板特征信息输入到标准模型库，我们将得到指定船舶的甲板数学模型库（图6所示）。

指定船舶的甲板数学模型库包含甲板数学模型集、边界条件、甲板模型索引，其中边界条件指所有甲板的边界条件集合，这样有利于集中比较挑选甲板模型；甲板模型索引用于在完成边界条件对比后，按照索引查找相应的甲板模型。甲板模型库以文件形式存储在计算机上，其包含3个部分：一个接收贯穿件重心点用于计算定位高度的可执行模块；一个接收贯穿件重心点用于边界条件比较，选择甲板模型的可执行模块；以及一个定义甲板模型与边界条件对应关系的索引文件。

2.3.2 计算机程序辅助计算流程

在船舶的甲板模型库建立后，使用Tribon自带的Vitesse类库中的kcs_draft、kcs_dex类函数，在Tribon交互界面下通过点选贯穿件模型获取模型的重心点，将该重心坐标发送到甲板数学模型库的边界条件判断模块，边界条件模块根据该船各甲板模型的边界定义条件选择出符合要求的甲板模型，并依据甲板模型索引找到对应的甲板数学模型方程，最终计算出指定贯穿件的定位尺寸。其处理流程如图7所示。

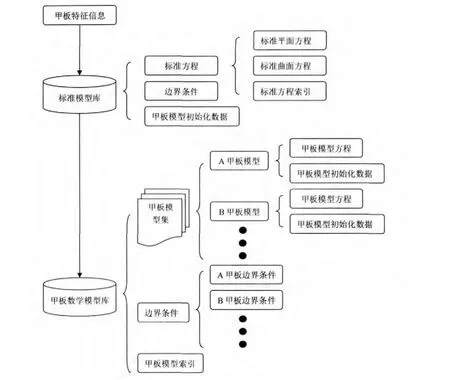
图6 甲板数学模型库结构

指定船舶的甲板数学模型库包含甲板数学模型集、边界条件、甲板模型索引，其中边界条件指所有甲板的边界条件集合，这样有利于集中比较挑选甲板模型；甲板模型索引用于在完成边界条件对比后，按照索引查找相应的甲板模型。甲板模型库以文件形式存储在计算机上，其包含3个部分：一个接收贯穿件重心点用于计算定位高度的可执行模块；一个接收贯穿件重心点用于边界条件比较，选择甲板模型的可执行模块；以及一个定义甲板模型与边界条件对应关系的索引文件。

2.3.2 计算机程序辅助计算流程

在船舶的甲板模型库建立后，使用Tribon自带的Vitesse类库中的kcs_draft、kcs_dex类函数，在Tribon交互界面下通过点选贯穿件模型获取模型的重心点，将该重心坐标发送到甲板数学模型库的边界条件判断模块，边界条件模块根据该船各甲板模型的边界定义条件选择出符合要求的甲板模型，并依据甲板模型索引找到对应的甲板数学模型方程，最终计算出指定贯穿件的定位尺寸。其处理流程如图7所示。

图7 计算机处理流程

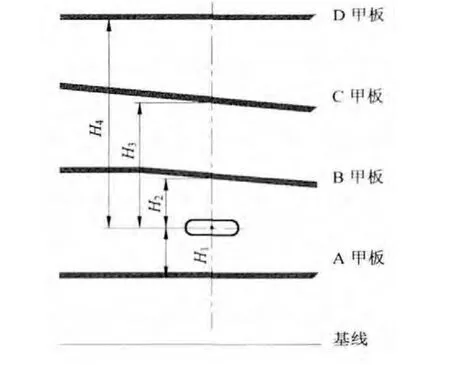
图8 贯穿件最终定位尺寸

在计算过程中由于船舶甲板是层叠式的，不同甲板在XY坐标平面上的边界定义常常相同，所以满足边界条件的甲板模型常常不止一个。图8所示贯穿件重心点满足4层甲板的边界条件，对于该贯穿件，经边界条件比较后将返回4个甲板模型：A甲板、B甲板、C甲板、D甲板的甲板数学模型。通过将贯穿件重心坐标代入这些甲板模型方程中计算，我们将得出1H、2H、3H、4H的值。通过比较能得出10H＜ 为负值，2H 为绝对值最小的正值，因此很快就能得出贯穿件距离顶部甲板尺寸为2H ，距离底部甲板的尺寸为1H- 。

3 实船使用效果

以本厂设计建造的 28000t多用途船为基础，将贯穿件普通定位方法与数学模型定位方法进行比较。依据该船的线性图可知，该船主甲板梁拱为200mm，罗经甲板梁拱为50mm，艏楼甲板脊弧为250mm，其他甲板均为水平甲板。利用普通定位方法时，由于该船甲板中有向X轴方向倾斜，也有向Y轴方向倾斜，所以除定义水平甲板高度以外，还要单独定义倾斜的甲板的补偿量。由于不同船舶的倾斜甲板的倾斜方向、倾斜角度都有可能不同，所以这种带有强烈单船特性的倾斜补偿定义文件，并不能在各船之间拷贝使用。并且对于不规则的倾斜甲板，该方法需要在倾斜补偿文件中定义大量的补偿项目，稍有不慎就会导致后期的贯穿件定位高度错误。而使用数学模型定位方法时，只需要将该船各甲板上任取的不在同一直线上的3个点的坐标以及甲板边界信息输入到标准模型库中，就建立了该船的甲板模型库，无需考虑甲板的倾斜方向。在铁舾件安装图出图时，对图面中处于任意位置的贯穿件都能准确给出其定位高度。

依据上述对比测试，发现普通定位方式需要定义繁杂的船体甲板信息，并且其他船模不能借鉴拷贝使用这些信息；对处于结构复杂位置的贯穿件的定位，其作用有限，仍然需要手工测量。运用数学模型定位新方法后，多个船模工程可以共享标准数学模型库，对任意甲板只要输入其甲板特征信息就能得到特定船的甲板模型库，而且对于船体的任何修改，只要输入修改后甲板的特征点坐标，就能马上更新该船的甲板模型库。所以无论是准确性还是易用性方面，基于数学模型的贯穿件定位方式都比之前的定位方式具有更大的优越性。

4 结 语

基于数学模型的贯穿件定位方法应用于结构复杂位置的贯穿件定位时，产生了较好的效果，并且该方法对管系、铁舾装等专业的三维模型的定位也具有参考意义。与此同时，发现该方法需要人工输入、更新甲板特征信息，使数据的准确性和实时性受到人为因素影响。所以如果能在船体结构建模时，令系统自动生成甲板、舱壁等结构的特征信息，那么船舶的数学模型就能在船体结构完成时自动建立，并且根据船体结构的更改自动更新，这样就降低了数学模型建立中的人为因素干扰，保证模型的准确性和实时性。

[1] 龙承业. 《解析几何》[M]. 北京：北京大学出版社，2004.

[2] 同济大学数学系. 《线性代数》[M]. 北京：高等教育出版社，2006.