行星齿轮传动中滚子轴承的寿命计算模型

谭 昕

（江汉大学 机电与建筑工程学院，湖北 武汉430056）

滚子轴承在风力发电机增速箱（以下简称增速箱）中大量使用，同时也是增速箱中故障率最高的零部件。据统计，风力发电系统故障70%来源于轴承失效，尤其是行星架前端、后端轴承的故障率约占轴承失效的90%［1］，其主要失效形式是点蚀和胶合。因此，有效、快速预测增速箱中轴承的使用寿命是一个重要的课题。

本文首先运用Lundberg－Palmgren方法建立滚子轴承的准动力学方程，计算滚动体的滑动率及内、外圈滚道的载荷分布；然后，建立增速箱系统的多体动力学模型，通过对动态行为的分析计算轴承的预期寿命及相关参数，并将两种计算结果进行了对比。

1 轴承准动力学方程的建模与计算

图1 增速箱的传动原理简图

图1是某型1.5兆瓦风力发电机增速箱传动链简图。本文的研究对象是该齿轮箱中行星架上风端（即前端）轴承的寿命。增速箱的主要传动参数如表1所示。

____________表1 增速箱主要传动参数

假设轴承受到叶轮的轴向力为Fa，轴承的径向载荷用Fr表示，围绕轴向的倾覆力矩用Mr表示，则轴承滚动体所承受的最大载荷为：

式（1）中：Qmax为所有滚动体中的最大载荷，Dpw为滚动体所在的节圆直径，α为轴承内、外圈之间的轴向偏转角；Z′为在某个方向上承受轴向力的滚动体数目。

根据 Lundberg－Palmgren理论［2］，轴承滚动体所受载荷的分布情况计算流程如下：

1）首先计算轴承滚动体在轴向外载荷和内、外圈倾覆力矩联合作用下所承受的复合载荷；

2）计算轴承滚动体在径向载荷单独作用下所承受的载荷；

3）将上述两个计算结果进行联立求解，获得其矢量和即为整个滚动体的载荷分布。

图2 轴承滚动体的接触载荷计算模型

如图2所示，根据弹性接触力学理论［3］，在倾覆力矩和轴向载荷复合作用下第j个滚动体的接触载荷为：

式中：Qαmax1、Qαmax2为滚动体在轴向承受的最大载荷；φj为滚动体位置角；θ 为轴承倾斜角；δαmax1、δαmax2为滚动体的最大轴向变形；j＝1，2，…，Z′；若轴向力作用方向为正，Qαmax1、Qαφj1和δαmax1为正；Qαmax2、Qαφj2和δαmax2为正。

当Fα＝0，Mr＝0时，Qrmax＝Qmax，则滚动体的径向载荷分布可由下式计算：

上式中：Qrmax为滚动体所承受的最大径向载荷；Qrφj为第j个滚动体所受到的径向载荷。

本文根据Lundberg－Palmgren理论及其计算步骤在Matlab环境下编程，以行星架前端轴承为例进行计算。行星架前端轴承采用SKF 230／530CA／W33双排调心圆柱滚子轴承，轴承材料为G20Cr2Ni4，弹性模量为206GPa，泊松比0.3，许用接触应力650MPa，受力计算结果如表2所示。

表2 行星架前端轴承受力计算结果

轴承的12个滚动体位载荷分布如图3所示。

图3 轴承滚动体载荷分布

从图3可以看出，轴承的第一和第十二滚动体位载荷最大，分别达到1.46GPa和1.17GPa，这只是名义载荷，而实际载荷谱的峰值可以达到名义载荷的3倍以上，并且反转的最大载荷值也可以达到名义载荷的2倍以上。在实际载荷远大于名义载荷的情况下，轴承内外圈滚道出现应力集中的概率会大幅提高，这种现象尤其容易出现在第一级行星架上。因为第一级行星架采用双壁式中空结构，其结构刚度较差，同时承受的扭矩载荷较大，因此本身容易出现偏心的情况，从而导致轴承产生位错，加剧应力集中的发生。图4是同一滚动体在不同滚动体位的载荷分布。

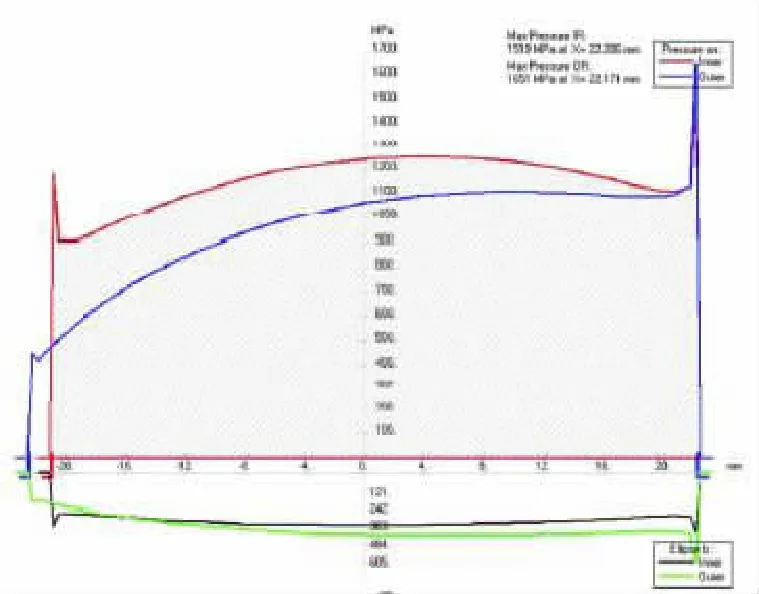
图4 滚动体在不同位置时的载荷分布

从图4可以看出，滚动体在第一和第十二滚动体的位置上存在较大的应力集中现象，其应力幅值较一般位置滚动体为大，且变化剧烈。

表3 轴承的计算寿命及当量动载荷

表3所示为轴承的计算寿命、当量动载荷及计算时间。从表3可以看出，轴承的参考寿命为14595小时，约为1.66年。通常风力发电机系统的设计寿命为15年，3年一次大修，因此该轴承没有达到设计要求。

2 增速箱的虚拟建模与轴承寿命动态仿真计算

为了验证准动力学方程的计算结果，本文在RomaxWind环境下建立整个增速箱系统的虚拟模型，通过动态仿真来计算轴承的预期寿命。RomaxWind是英国RomaxTech公司出品的一个基于多体动力学的大型数值仿真软件，其中带有大量轴承校核函数。

在RomaxWind环境中，可视为刚体的零部件，如轴、齿轮等，可以直接调用相应模块进行建模；而柔性体零部件，如齿圈、轴承、齿轮箱等，则需要在有限元软件（如Ansys）中建模并划分网格后，以IGES文件格式导入RomaxWind。增速箱的虚拟建模结果如图5所示［4］。

图5 增速箱的虚拟模型

在RomaxWind环境下对增速箱整机进行动态仿真，然后调用轴承分析函数对轴承滚动体载荷分布进行分析。虚拟模型中选用的轴承仍然是行星架前端轴承，其类型同样为SKF 230／530CA／W33双排调心圆柱滚子轴承，技术参数与上文相同。滚动体载荷分布如图6所示。

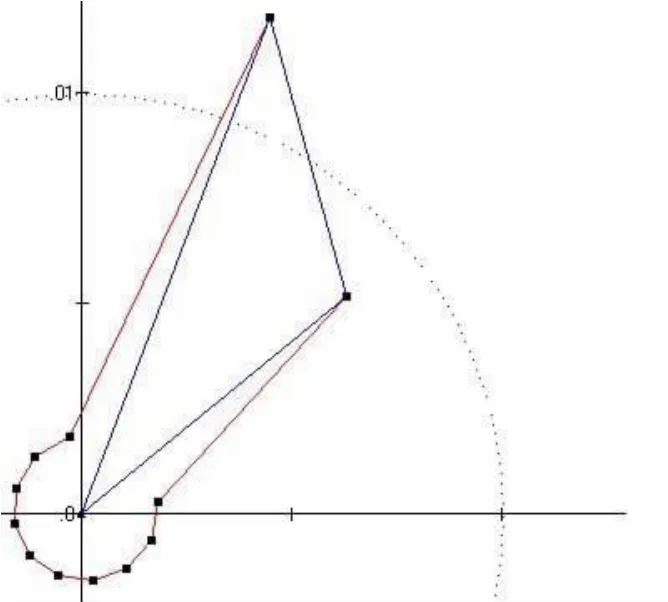
图6 轴承滚动体载荷分布

从图6中可以看出，第一和第十二滚动体位载荷仍然最大，分别为1.52GPa和1.13GPa。与图3相比，不同之处在于第一滚动体位的载荷大于第十二滚动体位。RomaxWind软件同时提供出轴承内外圈滚道的载荷分布，分别如图7和图8所示。

图7 内圈滚道载荷分布情况

图7所示为轴承内、外圈之间产生0.15°倾斜时，轴承内圈滚道上载荷分布情况。轴承内、外圈之间的倾斜会导致各滚动体与内、外滚道之间的接触力与切向拖曳力沿轴向非均匀分布，从而导致滚动体承受沿z轴的倾斜力矩，使滚动体两端与滚道挡边间产生接触力，这种接触力在外载荷的作用线上为最大，从图7中可以看出，第二十五滚动体位承受的接触力为4.3kN。产生这个载荷的主要原因就是风机叶轮在风力偏转载荷的作用下，轴承内外圈产生较大倾斜，导致接触力的变大［5］。

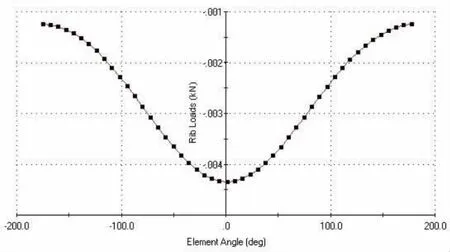
图8 外圈滚道载荷分布情况

图8为外圈滚道上载荷分布情况。由于外载荷的下降和主轴转速的上升，滚子保持架的打滑度会有所上升，产生这一现象的原因是因为轴承内圈对滚动体产生的拖曳力矩下降；另一方面，较大的滚动体产生的离心力又会使轴承外圈对滚动体产生的阻力矩增大；滚动体在刚刚脱离承载区时具有最小打滑度，而滚动体在进入承载区附件后会有最大打滑度。这是因为非承载滚动体只受到外滚道产生的阻力矩。由于滚动体和内、外圈滚道之间必然存在润滑油膜，所以所有滚子都有打滑现象，仍然需要通过提高轴承滚道及滚子的形状精度和表面精度来改善润滑效果。

表4 轴承的计算寿命及当量动载荷

对比表3和表4对应项的数值可知，对于两种计算模型而言，轴承计算寿命前者比后者小约4%，而轴承当量动载荷前者比后者大5.31%。这说明两种计算模型的计算结果是吻合的，但轴承准动力学方程所用的计算时间比RomaxWind软件的时间要少30.66%。

3 结论

本文分别运用轴承准动力学方程模型（集中质量模型）和多体动力学模型（有限元模型）对某型兆瓦级风机齿轮增速箱行星架前端轴承进行了寿命预测和当量动载荷计算，并分析了轴承上载荷分布规律及其对轴承寿命的影响，记录了计算时间。计算结果表明：

1）风力发电机叶轮的偏转对行星架前端轴承的寿命有较大影响，是导致轴承烧蚀、胶合失效的主要原因；

2）两种计算模型获得了相近的计算结果，偏差不超过6%，但轴承准动力学方程方法具有更快的计算速度，适合大计算量的场合。

［1］王素霞.国内外风力发电的情况及发展趋势［J］.电力技术经济，2007，19（1）：29－31.

［2］Kahraman A，Kharazi A A，Umrani M.A deformable body dynamic analysis of planetary gears with thin rims［J］.Journal of Sound and Vibration，2003，262：752－768.

［3］吴林丰，方宁.高速向心滚子轴承准动力学分析［J］.南京航空航天大学学报，1993，25（3）：330－340.

［4］徐亮，杨文涛.RomaxDesigner建模与分析实例［M］.北京：化学工业出版社，2008.

［5］杨威启.高速轻载圆柱滚子轴承分析［J］.轴承，1999（10）：3－6.