阶梯型圆盘的指向性及相关因素研究

贺西平，马奶连，赵凌波

（陕西师范大学 物理学与信息技术学院，陕西 西安710062）

20世纪70年代，Ggallon等人提出了弯曲振动辐射体［1］，因实际中有大量的应用［2－9］，有关这种类型辐射体的振动性能以及声学性能的研究一直没有间断．回顾这种振动体形式的演变过程，围绕的大多是其指向性、大功率、辐射效率、辐射阻抗等问题展开研究的［10－17］．弯曲振动辐射体的特点是辐射面积大，机械阻抗能与空气介质匹配较好，再加之在其中心驱动的振动体是一个高效大功率夹心换能器，因此能比较容易地向空气中辐射强超声．

起初提出的是弯曲振动平面辐射体，虽然它与空气介质匹配问题不大，但由于在盘面振动节线的两侧位相相反，将导致在声场振动干涉相消，经测试后的指向性不尖锐，另外声场相消的结果也造成声能量的浪费．为避免相位相消，在节线两侧沿着直径方向间隔上凸或下凹的阶梯盘，凸起或下凹的高度等于辐射介质中的半波长．这样改进的阶梯盘，理论上来看无论从指向性角度，还是效率角度都是最佳．经测试，阶梯盘的指向性犹如活塞辐射的盘面一样［1，15］．指向性是描述辐射体性能的一个很重要的参数［18－20］．仔细分析这种类型的辐射体，因其相邻的节线之间的各振动面元的振幅毕竟与活塞振动均匀时不同，是有一定起伏的，而且上凸或下凹的阶梯盘面又不在一个平面上．正因为辐射表面不在同一几何平面上，指向性计算显得很复杂，已有文献对其指向性作过一定的测试［15］，未见到过解析方法计算的文献，这不利于对辐射盘的优化设计和对其性能的综合评价．本文将阶梯盘分成两个部分，一部分为节线之外的圆环形盘，另一部分为节线以内的圆形盘，在阶梯圆盘的弯振频率上，从其实际模型出发，计算研究了声场的指向性．利用指向性解析表达式研究指向性与材料组成、基底厚度之间的关系，为计算和优化设计这种辐射体得出一些有用的结论．

1 指向性计算

为简化计算，考虑有一条节线的阶梯形薄圆盘，假设其一面置于无限大刚硬障板上，向另一面的介质中辐射声波，如图1所示．可认为节线把该阶梯盘分成了两个部分，一部分为节线之外的圆环形盘，其

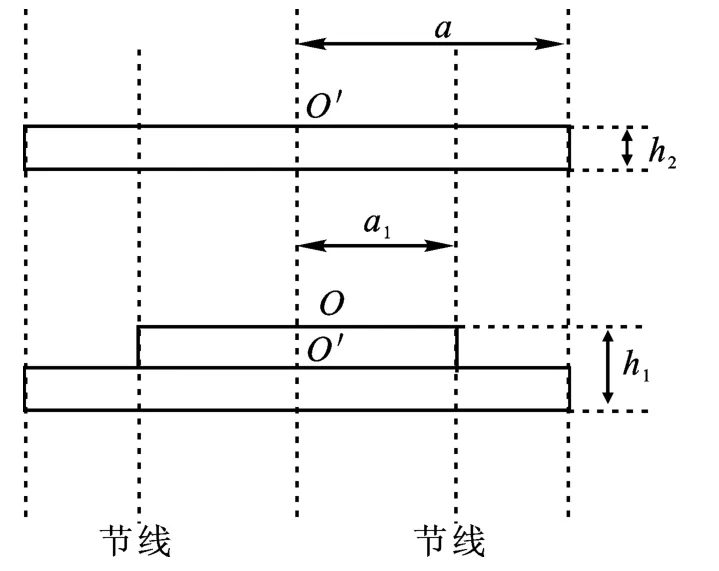
图1 一个节线的上凸阶梯圆盘Fig．1 The stepped circular plate with single raised step

1．1 节线以内的圆心盘产生的辐射声压场

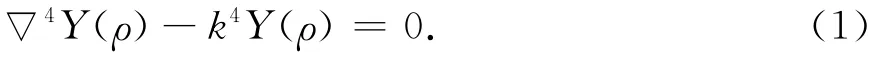
微分方程（1）式的一般解为［21］：

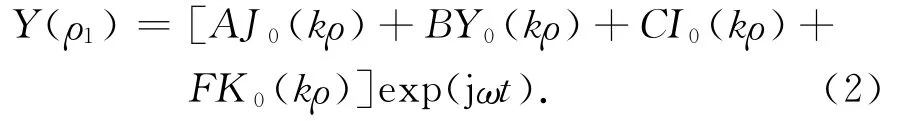
其中J0，Y0是一类和二类零阶贝塞尔函数，I0，K0是一类和二类零阶修正贝塞尔函数．对圆心盘，因为在中心处ρ1＝0的Y0和K0函数为无穷大，实际上是不可能的，故应取系数B和F为零．这样，圆心盘的表面位移和振动速度分别为

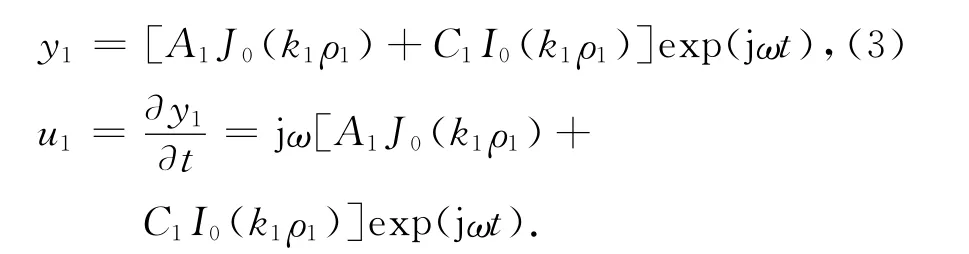
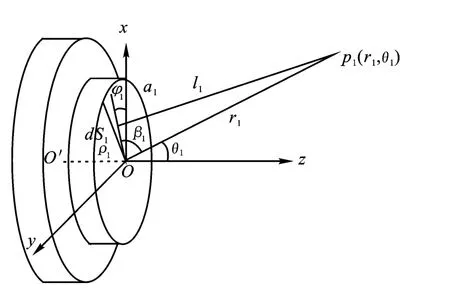
图2 阶梯盘的中心部分 －圆心盘的辐射声场示意图Fig．2 The schematic of radiated sound field at the central area of the stepped plate

速度振幅为

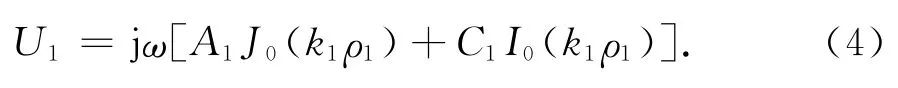
式中，k41＝ （ρvh1ω2）／D，D＝Eh31／12（1－σ2），ρ1∈［0，a1］．圆心盘产生的辐射声压为

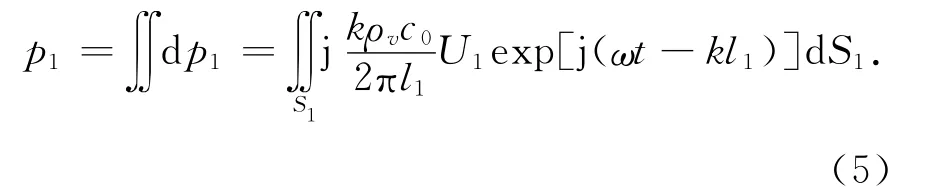
其中l1是圆心盘表面上的点源dS1到远场点的距离，ρvc0和k是传播介质中的特征阻抗和波数．因r1≫a1，（5）式中的分母中的l1可以用r1近似替代．由图2可看出，有以下的几何关系：

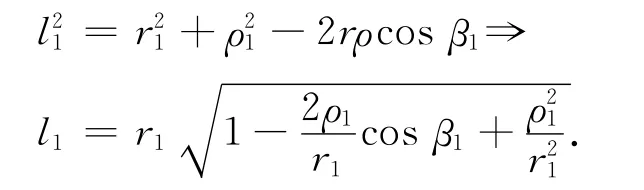
展开该式，因r1≫ρ1，l1可近似表示为l1＝r1－ρ1cosβ1．则（5）式变为

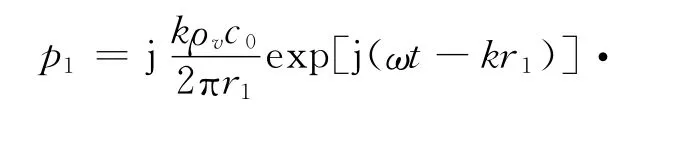
并由图2中可以发现如下的几何关系：

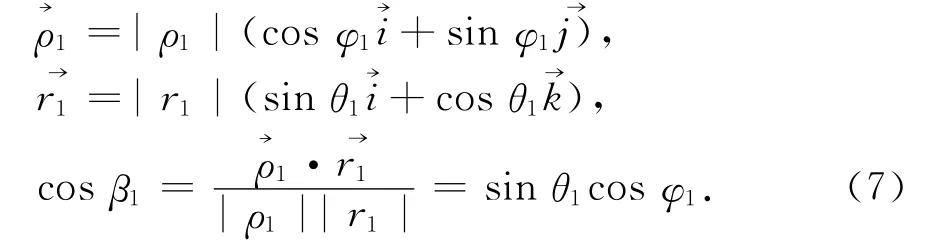
将（4）和（7）式代入（6）式中，得到

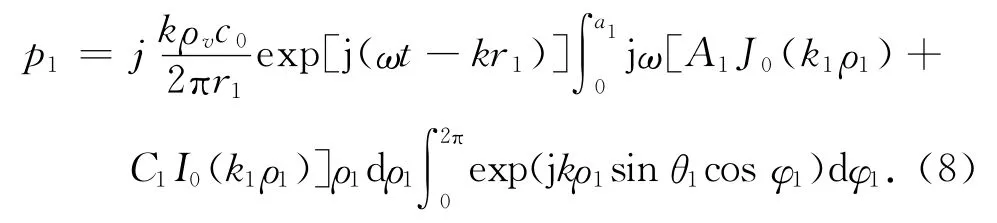
根据贝塞尔函数的性质

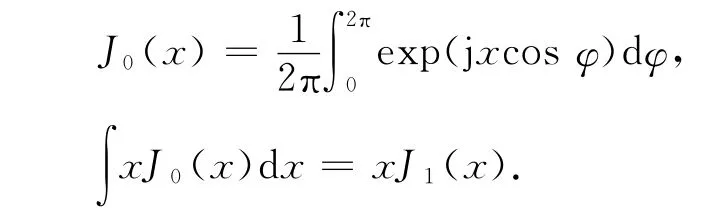
则（8）式可以写为

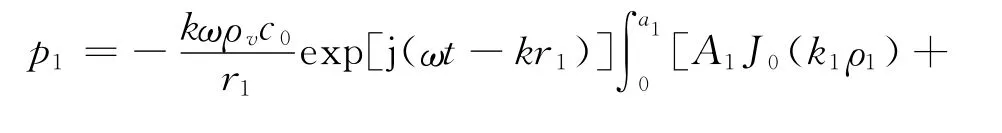
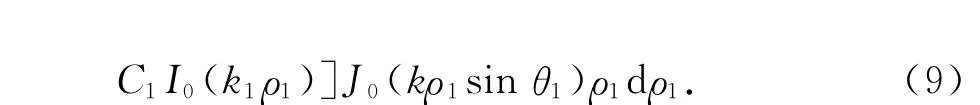
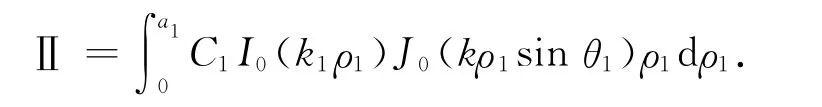
根据贝塞尔函数的积分性质

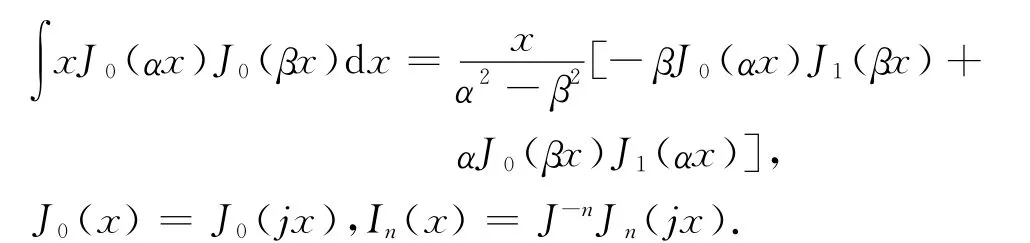
可以得到

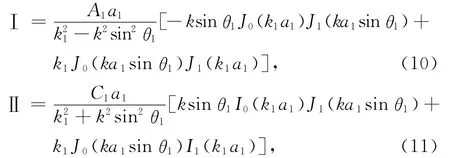
将（10）和（11）式代入（9）式中，则圆心盘的辐射声压为

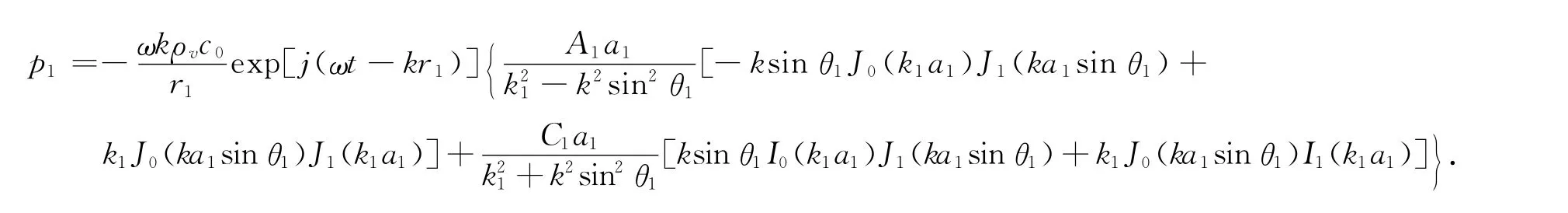
1．2 圆环形盘产生的辐射声压场

取圆环形盘上表面的中心为坐标原点O′，如图3所示．同理，由于其产生的辐射声场相对于穿过圆盘中心的z轴旋转对称，可以认为声场中的观察点p2（r2，θ2）位于xz平面上，该观察点离开原点距离为r2，位矢r2与z轴的夹角为θ2．

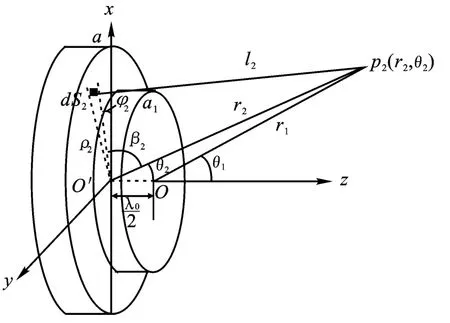
图3 阶梯盘圆环部分辐射声场示意图Fig．3 The schematic of radiated sound field in the circular ring of stepped plate

圆形盘面上的振动位移和振动速度分别为

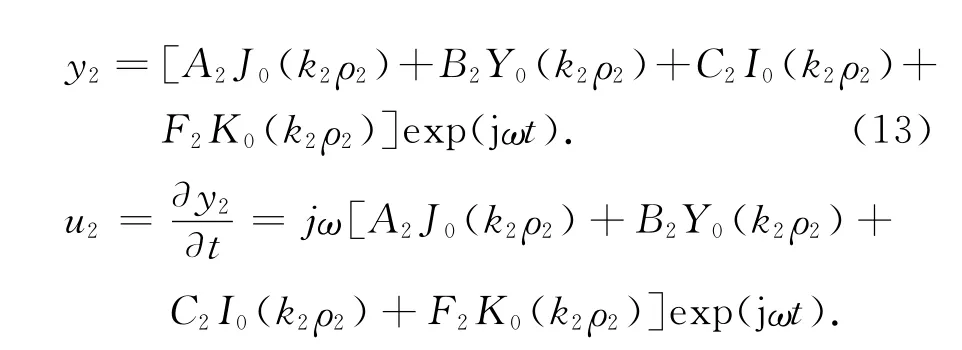
其中ρ2∈ ［a1，a］．

速度振幅为

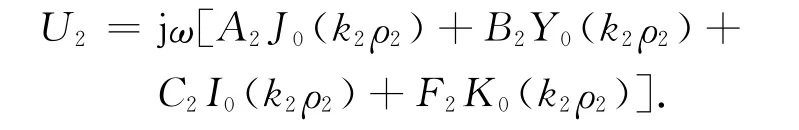
圆环形盘辐射产生的声压为

因r2≫a，上式中的分母r2可近似地被l2代替．由图3，有如下几何关系：

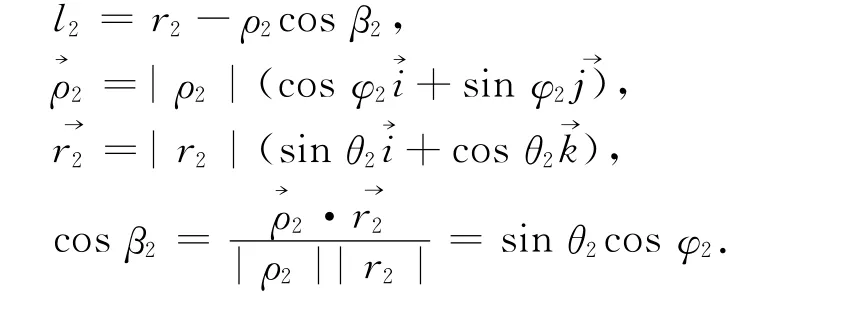
将上式代入（14）中，得

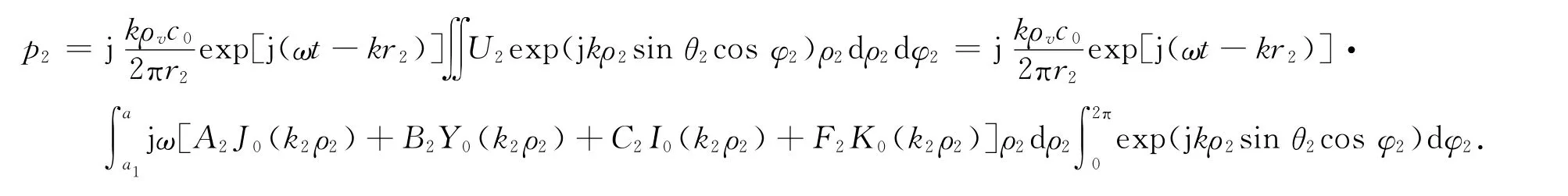
利用计算p1的相同方法，可以得到

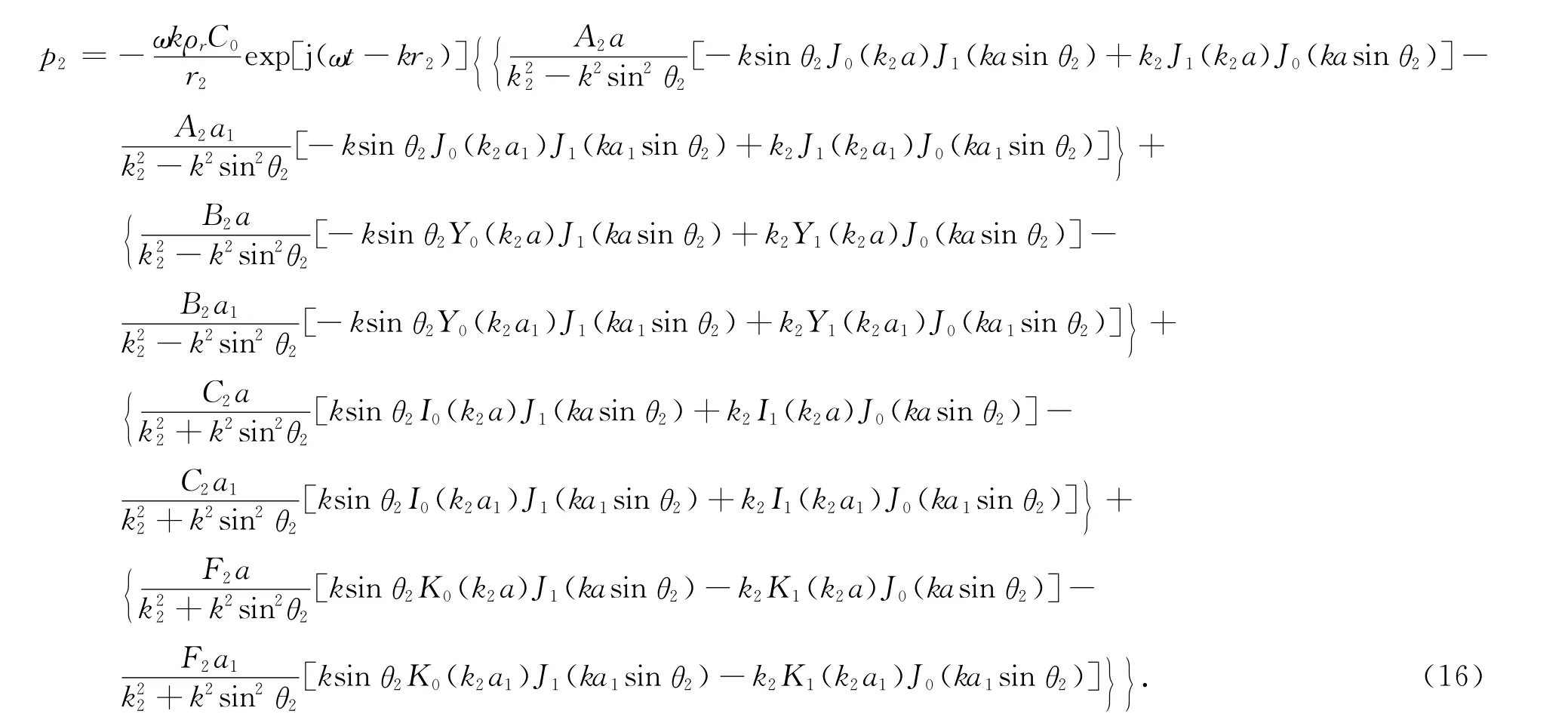
1．3 阶梯盘的辐射声场

远场点处，总的辐射声压即是由上面两部分的叠加：

令r2＝r，θ2＝θ，

因r1≫a1，r2≫a，

对上式中振幅部分可取θ1＝θ2，r1＝r2，相位部分，由图3可得到几何关系为

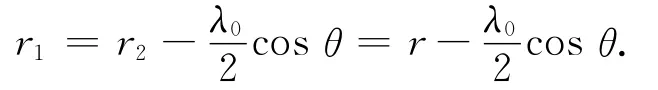
代入（1）式中，得到

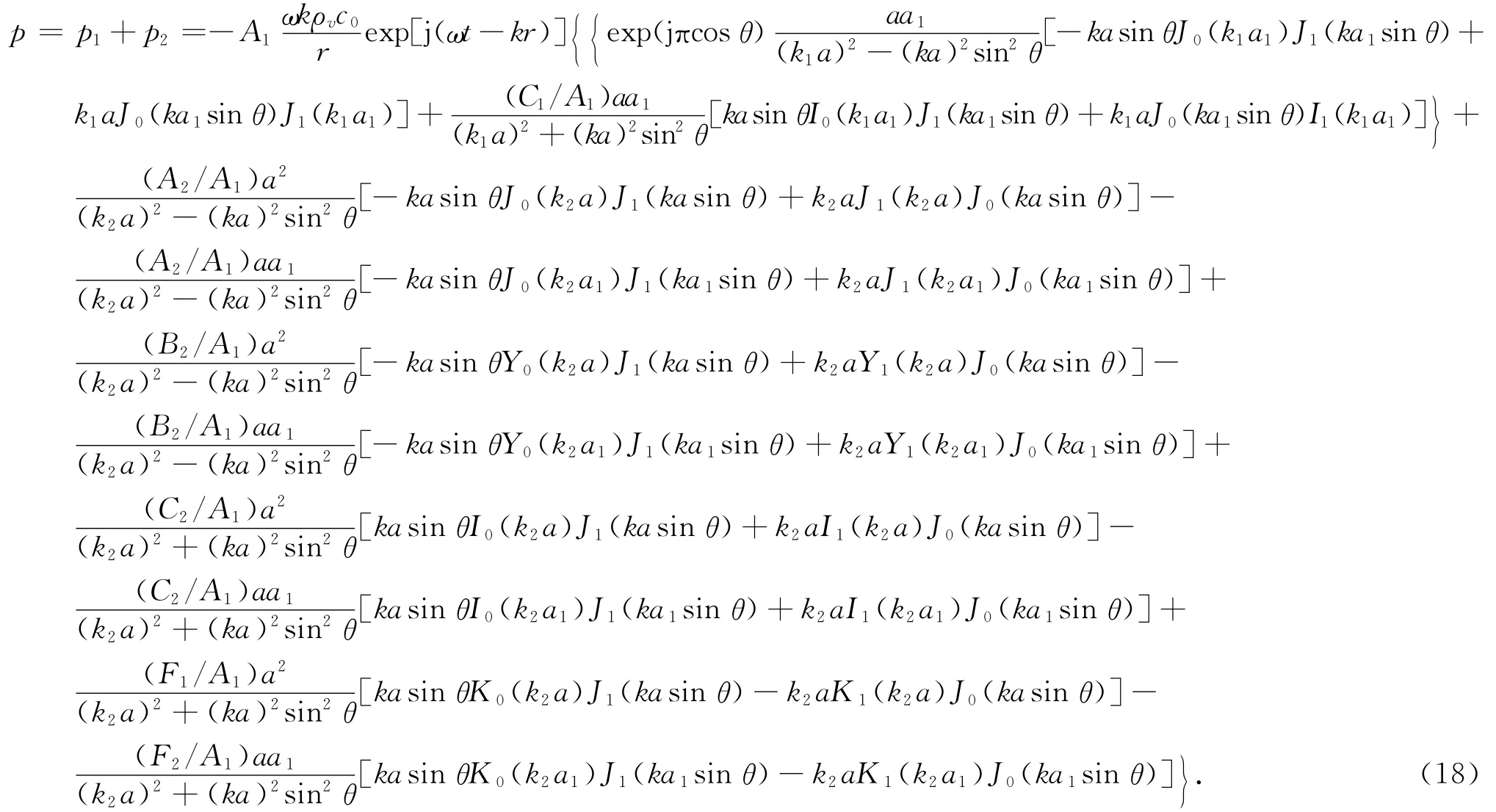
令θ＝0，可得

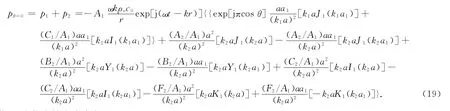
因此，圆盘指向性表达式为

这里，pa代表声压振幅．C1／A1，A2／A1，B2／A1，C2／A1，F2／A1为（18）和（19）式中的五个振型系数，可由节线处ρ1＝ρ2＝a1的四个连续条件和边界处ρ2＝a的两个自由条件得到［22］．

2 指向性与频率、材料及几何尺寸之间的关系

2．1 与频率的关系

计算的圆盘材料为铝合金，基底厚度为7 mm时，频率对应为10kHz、36．5kHz、45kHz、100kHz时一条节线盘的指向性．几何参数及计算得到的5个振型系数如表1所示，指向性如图4所示．取空气中声速c＝340m／s．

表1 不同频率下的振型系数＊Tab．1 The coefficients of vibration modal with different frequency

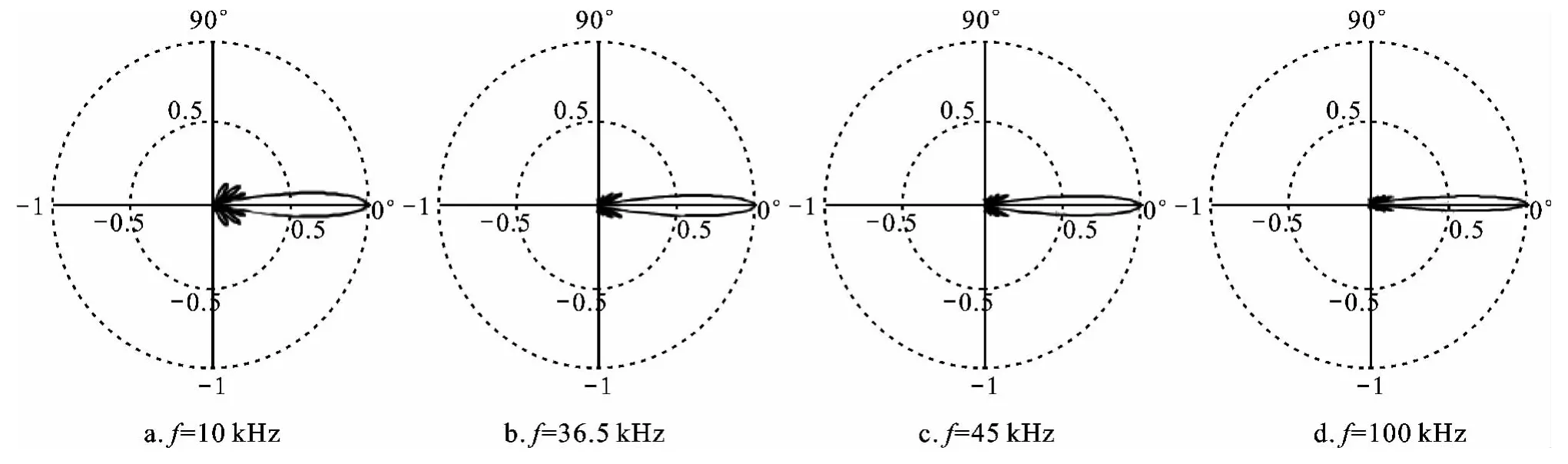
图4 表1中的四个阶梯盘的指向性图（阶梯盘材料为铝合金）Fig．4 The directivity of the four stepped plates in the table 1（material：Aluminum alloy）

2．2 与材料的关系

在同一弯曲振动谐振频率下（这里为36．5 kHz），计算了一条节线的钢、铜、镍材料阶梯盘的指向性，并与上面2．1中的铝合金材料进行比较．相应的几何参数及计算得到的振型系数见表2，指向性如图5所示．

表2 不同材料的振型系数＊Tab．2 The coefficients of vibration modal with different materials

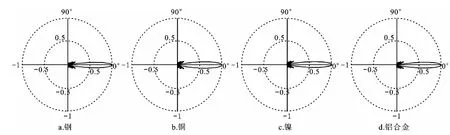
图5 表2中的四个阶梯盘的指向性图（谐振频率为36．5kHz）Fig．5 The directivity of the four stepped plates in the table 2（resonance frequency：36．5kHz）

2．3 与几何尺寸的关系

计算的圆盘材料为钢，频率为36．5kHz，基底厚度对应为1mm、2mm、7mm、11mm时盘的指向性，并对不同基底厚度阶梯盘的指向性作了比较，如图6所示．计算的有关参数见表3．

表3 不同几何尺寸下的振型系数＊Tab．3 The coefficients of vibration modal with different base thickness

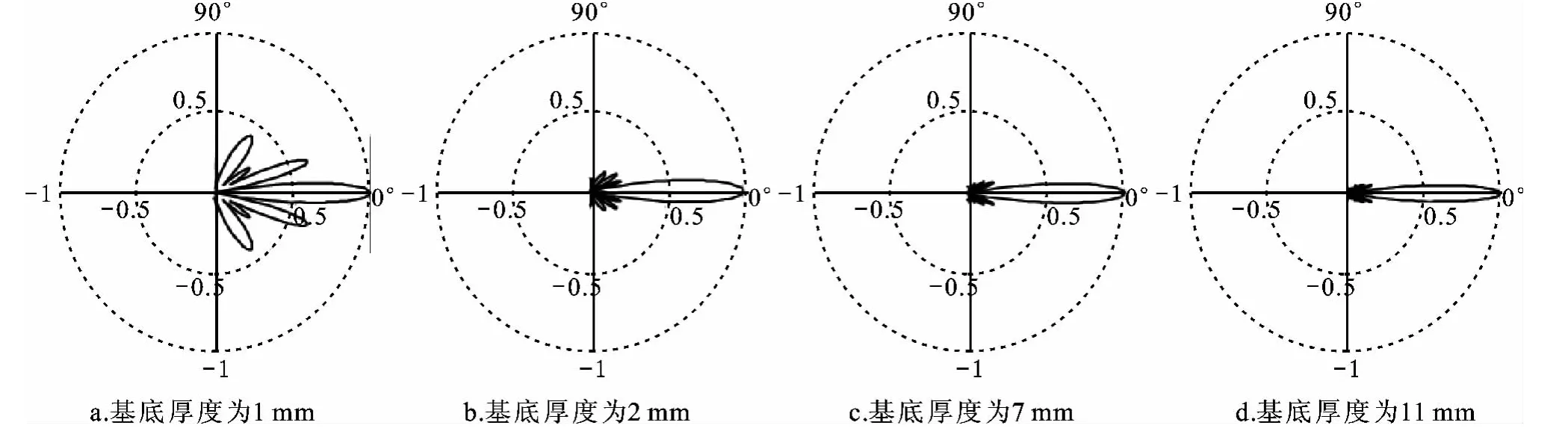
图6 表3中的四个阶梯盘的指向性图（谐振频率：36．5Hz，材料：钢）Fig．6 The directivity of the four stepped plates in the table 3（resonance frequency：36．5kHz，material：Steel）

3 结果与讨论

将上面解算得到的振型系数代入（20）式中，即可得到阶梯盘的指向性图案．

3．1 基底厚度为7mm、不同谐振频率铝合金材料的阶梯盘

图4a、b、c、d与文献［1］中图6在n＝1（一条节线）时，这4个对应频率上的测试结果几乎一致．从图4可看出，随着辐射频率的提高，阶梯盘的半径和节线半径将随之减小，主瓣则变得越来越尖锐．相比之下，弯曲振动平面辐射体的指向性较差，图7为文献［15］中测试的平面圆盘辐射体的一般指向性图．

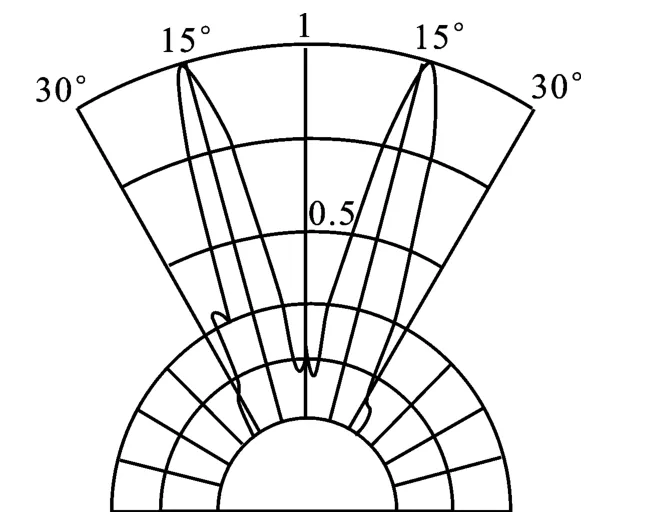
图7 平面圆盘辐射体的指向性图Fig．7 The directivity of the flat circular plate

3．2 谐振频率为f＝36．5kHz的不同材料阶梯盘

从图5，可以看出，对同一种谐振频率（为36．5kHz）、不同材料的指向性似乎无太大变化．这说明阶梯盘材料对指向性没有太大影响．

3．3 谐振频率为f＝36．5kHz的不同基底厚度的钢材料阶梯盘

从图6可以看出，对同一种谐振频率（这里为36．5kHz）、同一种材料的阶梯盘，基底厚度越厚，主瓣的指向性将越尖锐，副瓣似乎也变得窄细、尖锐起来．

4 结论

本文为阶梯圆盘的指向提供了一个计算方法．利用该方法，对弯曲振动阶梯盘的指向性进行了计算研究，计算结果与文献［10］的测试结果一致．文中进一步研究了阶梯盘指向性与材料、基底厚度等之间的关系．所得结论为：

（1）随着辐射频率的提高，阶梯盘的半径和节线半径将随之减小，主瓣则变得越来越尖锐，但副瓣也会随之增加．阶梯盘的指向性的确比平面盘的指向性要尖锐．

（2）同一种谐振频率、不同材料的阶梯盘，指向性变化不明显．指向性与阶梯盘材料关系似乎不大．

（3）同一种谐振频率、同一种材料的阶梯盘，基底厚度越厚，主瓣的指向性将越尖锐，副瓣也变得窄细、尖锐起来．

［1］Barone A，Gallego J A．Flexural vibrating free－edge plates with stepped thickness for generating high directional ultrasonic radiation［J］．The Journal of Acoustical society of America，1972，51（3）：953－959．

［2］Zheng Y，Zhang Q K．Simultaneous measurement of gas and solid holdups in multiphase systems using ultrasonic technique［J］．Chemical Engineering Science，2004，59（17）：3505－3514．

［3］Trinh E H．Compact acoustic levitation device for studies in fluid dynamics and material science in the laboratory and microgravity［J］．Review of Scientific Instruments，1985，56（11）：2059－2065．

［4］Collas P，Barmatz M，Shipley C．Acoustic levitation in the presence of gravity［J］．The Journal of Acoustical Society of America，1989，86（2）：777－787．

［5］Gallego J A，Rodr guez G，lvez J C G，et al．A new high－intensity ultrasonic technology for food dehydration［J］．Drying Technology，1999，17（3）：597－608．

［6］Pangu Gautam D，Feke Donald L．Acoustically aided separation of oil droplets from aqueous emulsions［J］．Chemical Engineering Science，2004，59（15）：3183－3193．

［7］Gonz lez I，Rodr guez J，Garmendia I，et al．Application of high intensity air－borne ultrasound for debubbling liquid coating layers［J］．Ultrasonics，2006，44（Sup．1）：529－532．

［8］Riera E，Gallego J A，Mason T J．Airborne ultrasound for the precipitation of smokes and powders and the destruction of foams［J］．Ultrasonics，2006，13（2）：107－116．

［9］Rodr guez G，Riera E，Gallego，et al．Experimental study of defoaming by air－borne power ultrasonic technology［J］．Proceedings of the Physical Society，2010，3（1）：135－139．

［10］Gallego J A．Axisymmtric vibrations of circular plates with stepped thickness［J］．Journal of Sound and Vibration，1973，26（3）：411－416．

［11］Gallego J A，Rodriguez G，Riera S E，et al．A macrosonic system for industrial processing［J］．Ultrasonics，2000，38（1／8）：331－336．

［12］Gallego－Juarez J A，Rodr guez－corral G，Gaete－Garreton L．An ultrasonic transducer for high power applications in gases［J］．Ultrasonics，1978，16（6）：267－271．

［13］Campos－Pozuelo C，Lavie A，Dubus B，et al．Numerical study of air－borne acoustic field of stepped－plate high－power ultrasonic transducers［J］．Acta Acustica united with Acustica，1998，84（6）：1042－1046．

［14］Gallego－Jurez J A，Rodriguez－Corral G，Riera－Franco de Sarabia E，et al．Recent developments in vibratingplate macrosonic transducers［J］．Ultrasonics，2002，40（1／8）：889－893．

［15］Gallego J A，Rodr guez G，Acosta V，et al．Power ultrasonic transducers with extensive radiators for industrial processing［J］．Ultrasonics Sonochemistry，2010，17（6）：953－964．

［16］Yub Je，Haksue Lee，Jongkyu Park，et al．A steppedplate bi－frequency source for generating a difference frequency sound with a parametric array［J］．The Journal of Acoustical society of America，2010，127（6）：3494－3502．

［17］贺西平．弯曲振动阶梯圆盘辐射阻抗的计算［J］．物理学报，2010，59（5）：3290－3293．

［18］张海澜．理论声学［M］．北京：高等教育出版社，2007：231．

［19］张成，陈克安，杨志兴．刚性圆柱体上圆阵波束形成性能分析［J］，声学学报，2010，35（1）：68－75．

［20］陈新华，蔡平，惠俊英，等．声矢量阵指向性［J］，声学学报，2003，28（2）：141－144．

［21］Gallego－Juárez J A．Axisymmtric vibrations of circular plates with stepped thickness［J］．Journal of Sound and Vibration，1973，26（3）：411－416．

［22］贺西平，宋旭霞，李伟．阶梯圆盘的设计及其声参数计算［J］．声学学报，2010，35（5）：502－507．