一类具有强Allee效应的捕食－食饵模型正平衡态解的存在性

臧 辉，聂 华

（陕西师范大学 数学与信息科学学院，陕西 西安710062）

群居有利于物种的生长和存活，但过分稀疏和过分拥挤都可阻碍其生长，从而对物种的生长繁殖产生副作用，每一物种都有自己最适宜的密度，这就是所谓的Allee效应［1］．近年来，具有Allee效应的物种捕食模型得到广泛研究．文献［2］研究了食饵具有强Allee效应的常微分方程模型，对该模型建立了全局双稳定分析；文献［3］利用上下解方法讨论了具有强Allee效应的反应扩散模型，得到了正平衡态解的存在性．本文研究下面具有强Allee效应的捕食－食饵模型：

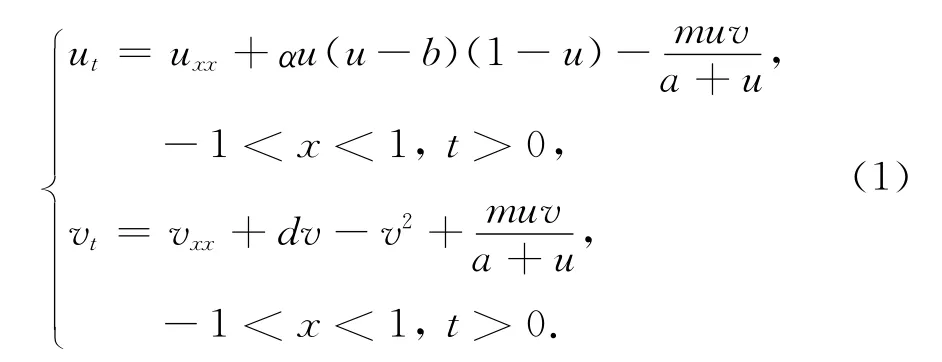
初边值条件为

其中，u、v分别表示食饵和捕食者的密度，参数a、m、α、b、d均为正常数且0＜2b＜1，α为u的内禀增长率，b为反映Allee效应强度的参数，d为v的增长率为HollingⅡ型的功能反应函数，m为相互作用系数，a为半饱和系数．由文献［4］知，对于模型（1），只有当食饵密度超过反映Allee效应强度的参数b时，食饵才能增长．文献［4］研究了齐次Neumann边界条件下模型（1）的动力学性质，证明了解的全局存在性，确定了解的全局渐近行为．研究结果表明，在齐次Neumann边界条件下，模型（1）的半平凡解为（b，0）、（1，0）、（0，d），其性质简单、明确．然而，在Dirichlet边界条件下，模型（1）形如（u，0）形式的半平凡解性质复杂，为研究模型（1）的平衡态解带来了困难，导致目前关于Dirichlet边界条件下，具有强Allee效应的捕食 －食饵模型的研究还比较少．本文研究Dirichlet边界条件下模型（1）的动力学性质．为此，研究如下平衡态系统

其中0＜b＜1／2．

1 局部分支解的存在性

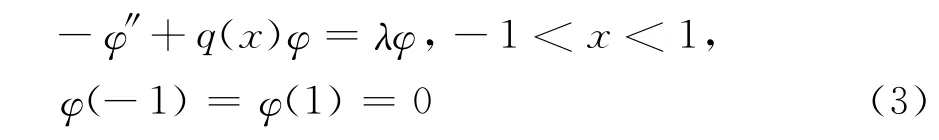
引理1［5］设q（x）∈C1［－1，1］，则特征值问题的所有特征值满足0＜λ1（q）≤λ2（q）≤λ3（q）≤ …→ ∞，相应的特征函数分别为φ1，φ2，φ3，…，其主特征值

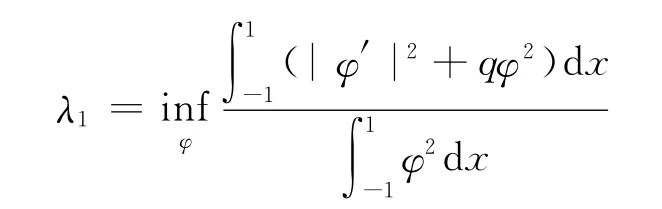
是单重的．而且有如下比较定理：若q1≥q2，则λj（q1）≥λj（q2）；若又有q1≢q2，则λj（q1）＞λj（q2）．记λ1＝λ1（0）．

考虑非线性边值问题

由文献［5］的定理3．3．28知，如果d≤λ1（q），那么0是方程（4）的唯一非负解；如果d＞λ1（q），方程（4）有唯一正解．特别地，当q（x）≡0时，如果d＞λ1，那么非线性边值问题

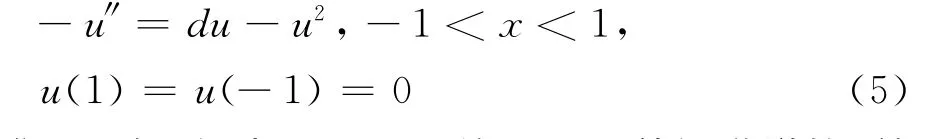
有唯一正解，记为θd，且θd关于d是单调递增的，并有θd＜d．显然，当d＞λ1时，系统（2）存在半平凡解（0，θd）．

考虑半线性边值问题

其中0＜b＜1／2是反映Allee效应强度的参数．文献［6－8］对方程（6）正解的存在性及个数进行了研究，所得结果如下：

引理2［6］设0＜b＜则存在α＊＞0，使得如下结论成立：

（ⅰ）当α＜α＊时，边值问题（6）只有0解；

（ⅱ）当α＝α＊时，边值问题（6）有1个非平凡解；

（ⅲ）当α＞α＊时，边值问题（6）有2个非平凡解，分别记为u＊1、u＊2，且u＊2关于α单调递增，u＊1关于α单调递减

（ⅰ）若α＞α＊，则系统（2）存在3个半平凡解（u＊1，0）、（u＊2，0）、（0，θd），且u＊1＜u＊2；

（ⅱ）若α＝α＊，则系统（2）仅存在2个半平凡解（u＊0，0）、（0，θd）．

引理3［7］设0＜b＜1）u＊2－b），则对于上述α＊＞0，当α＞α＊时，L10、L0均非奇异，且L0的所有特征值均小于0．

下面给出系统（2）正解的先验估计．

引理4 若（u，v）是系统（2）的正解，且u≢0，v≢0，0＜b＜1／2，则

（ⅱ）如果d＞λ1，那么v≥θd；

（ⅲ）存在M＞0，使得d＜M．

证明 （ⅰ）由极值原理知，u、v＞0（x∈（－1，1））．假 设 存 在x0∈ ［－1，1］使 得u（x0）＝，且u（x0）＞1，则x0∈ （－1，1），从而u″（x0）≤0．又 因 为u″（x0）＝au（x0）（u（x0）－b）（1－u（x0））＞0，矛盾．因此u≤1．下面证明v≤d＋．假设存在x1∈ ［－1，1］使得v（x0）＝，且v（x1）＞，则x1∈ （－1，1），从而v″（x1）≤0．另一方面－v″（x1）＝＜0，故v″（x1）＞0，矛盾，因此v≤d＋

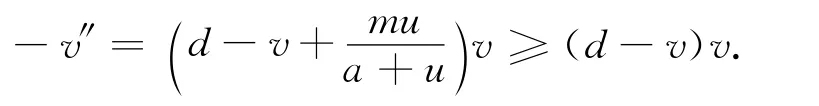
（ⅱ）当d＞λ1时，v和0为方程（5）的一对上下解，且v≥0，θd为（5）的唯一解，故由文献［5］的定理3．3．2知，v≥θd．

（ⅲ）假设存在di→ ∞ 及（ui，vi）为系统（2）在d＝di处的正解，则由（ⅱ）知，vi＞θdi．令K0⊂（－1，1），则由文献［9］的性质6．5知，θdi→ ∞，x∈K0，故vi→ ∞，x∈K0．

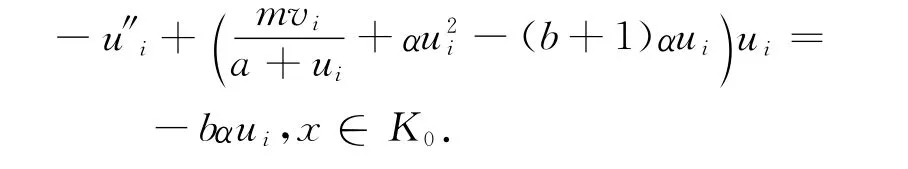
由于ui＞0从而－bα1）αu）i，但是矛盾，因此d有界．

令X＝C10［－1，1］×C10［－1，1］，固定α＞α＊，下面取d为分歧参数，从非负半平凡解分支｛（d；u＊2，0）：d＞0｝出发，构造系统（2）的正解．

定理1 设α＞α＊，0＜b＜1／2，则（λ；u＊2，0）为系统（2）的分歧点，且在（λ；u＊2，0）的邻域内，系统（2）存在正解，其中

证明 定义算子F（d；u，v）：R＋×X→X为

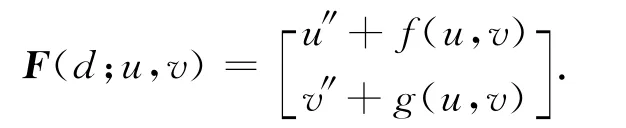
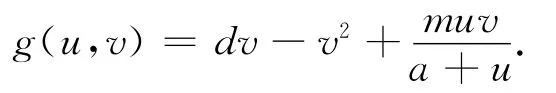
记F（λ；u，v）在（u＊2，0）处的Fréchet导数为L（λ；u＊2，0），则

其中fu（u＊2，0）＝α（－3u＊22＋2（b＋1）u＊2－b），

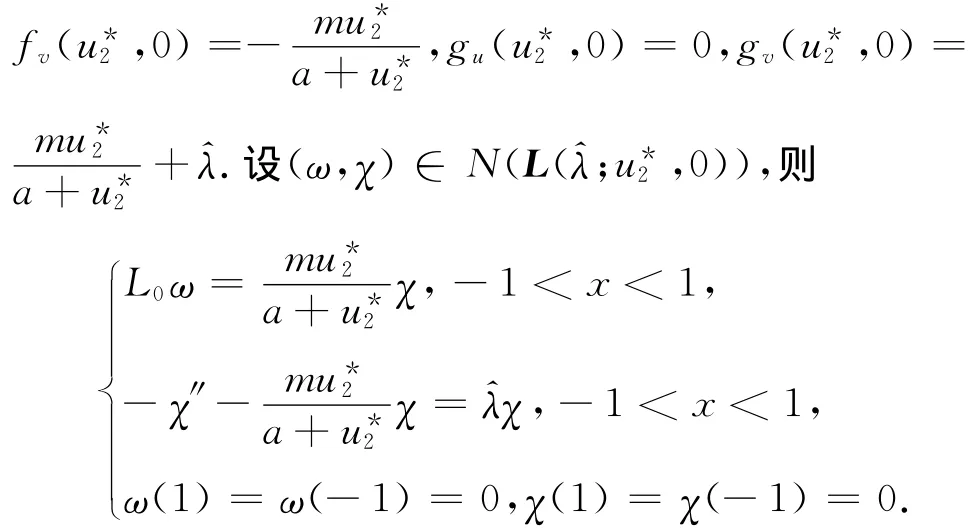
其中L0由引理3给出．若χ≡0，则由引理3知ω≡0，矛盾，故χ＞0．令λ相应的主特征函数为χ1，且假设χ1＞0，因此χ＝χ1，从而ω1＝且由广义极大值原理知ω1＞0，所以N（L（λ；u＊2，0））＝span｛（ω1，χ1）｝．另一方面，L（λ；u＊2，0）的伴随算子

L（λ；u＊2，0）（ω，χ）＝0等价于

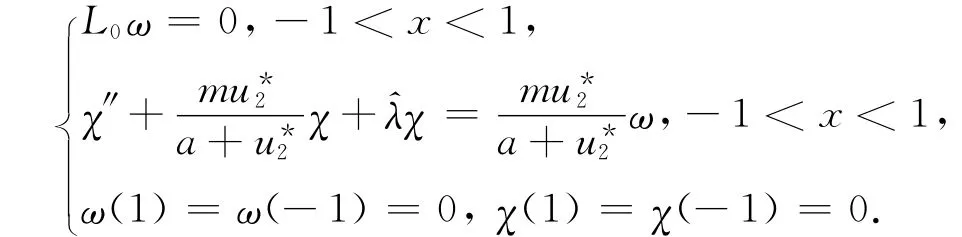
显然，ω≡0，χ＝χ1，从而N（L＊（λ；u＊2，0））＝span｛（0，χ1）｝．由Fredholm选择公理知

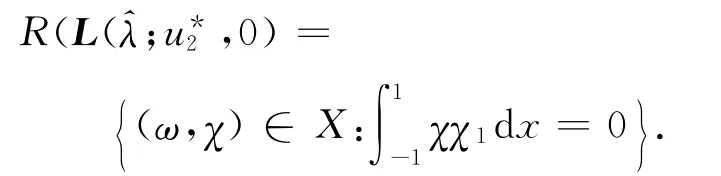
因此codimR（L（λ；u＊2，0））＝1．令L1（λ；u＊2，0）＝，则

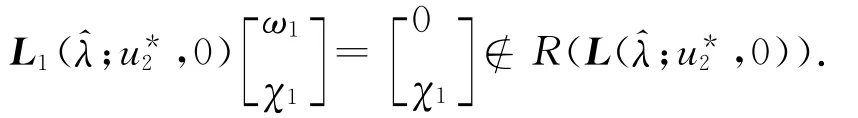
至此，简单特征值分歧定理的条件得到满足，故由文献［10］知，存在充分小δ＞0及C1连续曲线（d（s）；φ（s），ψ（s））：（－δ，δ）→R×X，使得d（0）＝λ，φ（0）＝0，ψ（0）＝0，且（d（s）；u（s），v（s））＝（d（s）；u＊2＋s（ω1＋φ（s）），s（χ1＋ψ（s）））满足F（d（s）；u（s），v（s））＝0，其中φ（s）、ψ（s）∈Z，X＝Z⊕N（L（λ；u＊2，0））．因此（d（s）；u（s），v（s））（｜s｜＜δ）是系统（2）的解分支，其中u（s）＝u＊2＋s（ω1＋φ（s）），v（s）＝s（χ1＋ψ（s））．若取0＜s＜δ，则它恰好是（2）的正解．而且，在分歧点（＾λ；u＊2，0）附近的非负解要么在分支｛（d；u＊2，0）：d＞0｝上，要么在分支｛（d（s）；u（s），v（s））：0＜s＜δ｝上．

2 局部分支解的延拓

本节借助于文献［11］中的全局分歧理论方法，将定理1给出的局部分支延拓为全局分支．为此令ω＝u－u＊2，χ＝v，若（u，v）为系统（2）的非负解当且仅当－u＊2≤ω≤1－u＊2，χ≥0，且满足

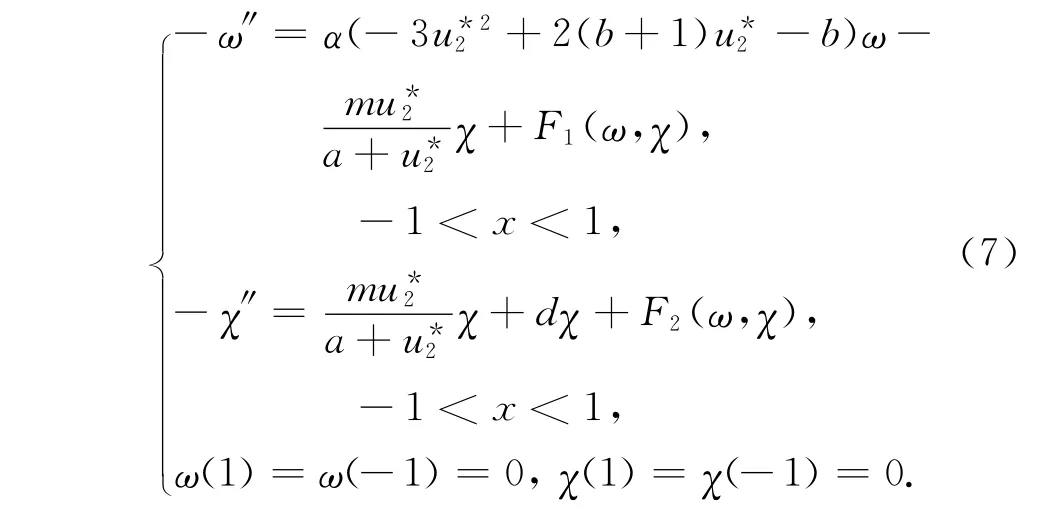
其中F1（ω，χ）＝αω2（3u＊2－b－1＋ω）＋F0＝ （F1，F2），F0（0，0）＝0，且F0关于（ω，χ）在（0，0）处的Fréchet导数D（ω，χ）F0｜（0，0）＝0．设K是－在Dirichlet边界条件下的逆算子，则（7）等价于

定义算子T：R＋×X→X为

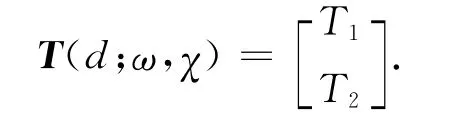
其中T1＝αK（－3u＊22＋2（b＋1）u＊2－b）ω－K·KF2（ω，χ），则T（d；ω，χ）为X上的紧可微算子．令G（d；ω，χ）＝ （ω，χ）T－T（d；ω，χ），则G是C1函数且G（d；0，0）＝0．易知，G（d；ω，χ）满足－u＊2≤ω≤1－u＊2，χ≥0的零点恰好是（2）的非负解．令

K（d）＝DT（ω，χ）（d；0，0）＝

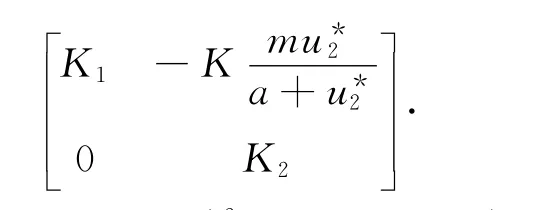
其中K1＝αK（－3u＊22＋2（b＋1）u＊2－b），

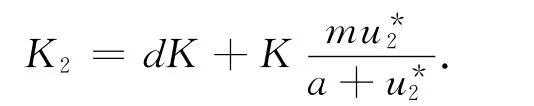
设η≥1是K（d）的特征值，相应的特征函数设为（ω，χ），则K（d）（ω，χ）T＝η（ω，χ）T，即

假设χ≡0，由于η≥1，则由文献［5］的定理3．3．11知即算的所有特征值全小于0，从而ω＝0，矛盾．因此χ≢0，于是存在某个i，使得d＝di（η），其中di（η）是问题的特征值，显然，di（η）关于η在［1，＋∞）上递增，且di（η）满足

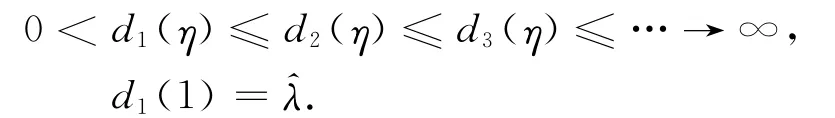
因此η≥1为K（d）的特征值当且仅当存在某个i，使得d＝di（η）．

假设d＜λ，则对任意的η≥1、i≥1，有d＜d1（1）≤di（η）．因此K（d）没有大于或等于1的特征值，从而当d＜λ时，index（T（d；·），0）＝1．

假设λ＜d＜d2（1），则对任意的η≥1、i≥2，有d＜di（η）．又d1（1）＝且d1（η）关于η严格递增，因此存在唯一的η1＞1，使得d＝d1（η1）．于是N（η1I－K（d））＝χ）｝，dim N（η1I－K（d））＝1，其中χ＞0是如下特征值问题的主特征函数：

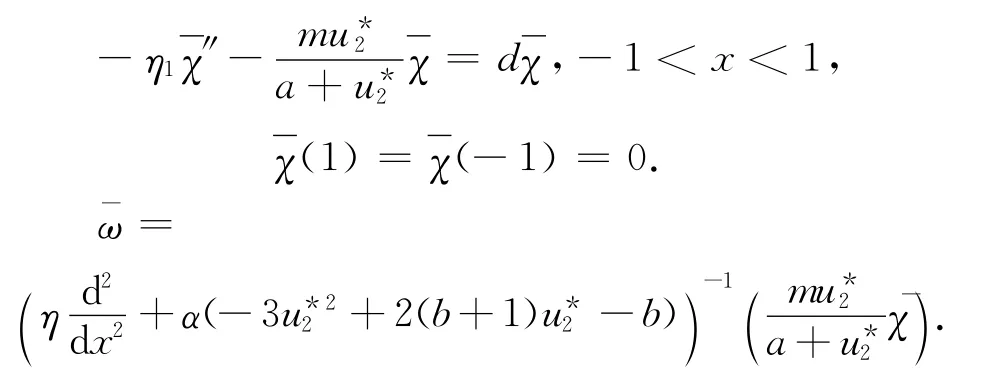
下面证明R（η1I－K（d））∩N（η1I－K（d））＝｛0｝．若不然，不失一般性，设（ˉω，ˉχ）∈R（η1IK（d）），则存在（ω，χ）∈X，使得（η1I－K（d））（ω，χ）＝（ˉω，ˉχ），即

在上述方程两端同时乘ˉχ，并在［－1，1］上积分得

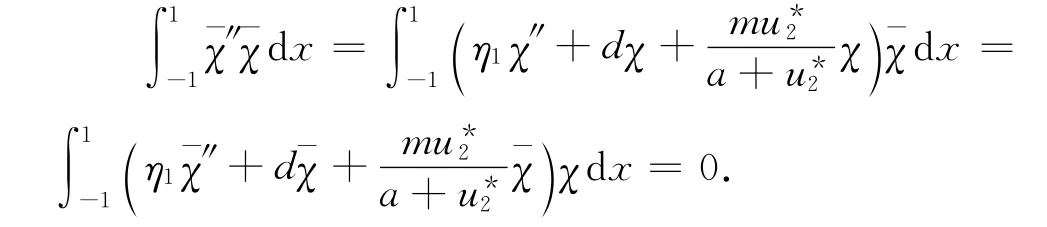
由全局分歧定理［10］知，在R＋×X内，存在从u＊2，0）出发的连通分支C0满足G（d；ω，χ）＝0，且在点（λ；u＊2，0）附近，G（d；ω，χ）的所有零点都在定理1给出的那条曲线上．令C1＝C0－ ｛（d（s）；s（ω1＋φ（s）），s（χ1＋ψ（s）））：－δ＜s＜0｝，C＝ ｛（d；u，v）：u＝ω＋u＊2，v＝χ，（d；ω，χ）∈C1｝，则C为系统（2）由（λ；u＊2，0）出发的解曲线．

令P1＝ ｛u∈C10［－1，1］：u（x）＞0，－1＜x＜x＝1，－1｝，P＝ ｛（d；u，v）∈R＋×X：u，v∈P1｝，则在（λ；u＊2，0）的邻域内有C⊂P，并且C－｛（λ；u＊2，0）｝满足下列条件之一：

（ⅰ）C连接了分歧点（＾λ；u＊2，0）和（d；u＊2，0），其中I－K（d）不可逆，且λ≠d；

（ⅱ）C在R＋×X内由（＾λ；u＊2，0）延伸到∞；

（ⅲ）C包含了形如（＾λ；u＊2＋u，v），（λ；u＊2－u，v）的点，其中（u，v）≢ （0，0）．

下面证明C－｛（λ；u＊2，0）｝⊄P．若C－｛（λ；u＊2，0）｝⊂P，则（ⅰ）和（ⅲ）不成立．另一方面由引理4知，存在常数M1＞0，满足‖u‖、‖v‖≤M1，即C在R＋×X中有界．因此（ⅱ）不成立．从而C－｛（λ；u＊2，0）｝⊄P，故存在（＾d；u，v）∈（C－｛（λ；u＊2，0）｝）∩∂P和序列｛（dn；un，vn）｝⊂C∩P，un、vn＞0，使得当n→ ∞ 时，（dn；un，vn）→ （d；u，v）．易知u∈∂P1或v∈∂P1．假设u∈∂P1，则u≥0，x∈ ［－1，1］，从而要么存在x0∈ （－1，1），使得u（x0）＝0，要么x0＝－1或1，使得0．由于u满足方程

其中M2＞0，满足0且有界．由极大值原理知u≡0．同理，假设v∈∂P1，则v≡0．因此（＾u，v）有以下4种可能：

假设（＾u，v）＝ （0，0），则当n→ ∞ 时，（dn；un，且满足

由Lp估计和Sobolev嵌入定理知，存在Un的收敛子列（不失一般性仍然记为Un）使得当n→∞ 时，Un→U在C10［－1，1］上成立，且U≥0，≢0，x∈（－1，1），因此对于上式令n→ ∞ 得

由强极值原理知U≡0，x∈ ［－1，1］，矛盾．

假设（u，v）＝ （0，θd），则当n→ ∞ 时，（dn；un，vn）→ （d；0，θd）．令Un＝且满足

由Lp估计和Sobolev嵌入定理知，存在Un的收敛子列（不失一般性仍然记为Un）使得当n→∞ 时，Un→U在C10［－1，1］上成立，且U≥0，≢0，x∈（－1，1）．因此对于上式令n→ ∞ 得

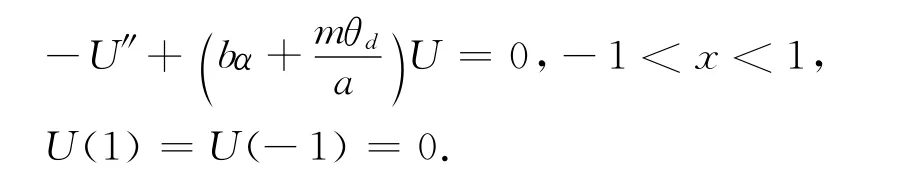
由强极值原理知U≡0，x∈ ［－1，1］，矛盾．

假设（u，v）＝（u＊2，0），则当n→∞时，（dn；un，vn）→（d；u＊2，0）．令Vn＝且满足

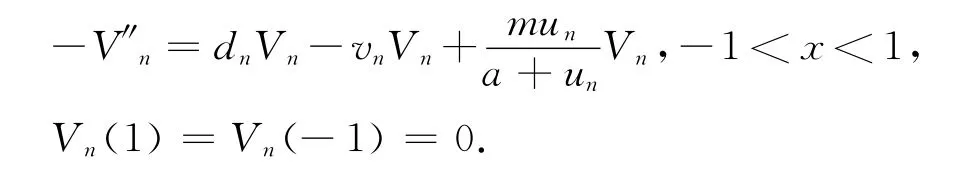
由Lp估计和Sobolev嵌入定理知，存在Vn的收敛子列（不失一般性仍然记为Vn）使得当n→ ∞时，Vn→V在C10［－1，1］上成立，且V≥0，≢0，x∈（－1，1）．因此对于上式令n→ ∞ 得

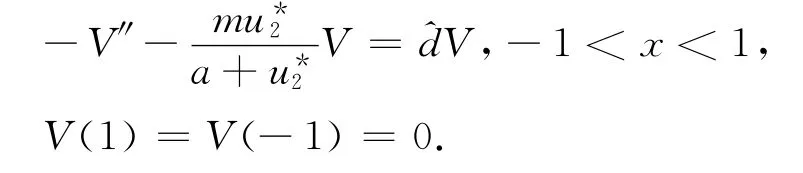
由极大值原理知V＞0，x∈（－1，1）．因此d＝λ，矛盾．

从而全局分支C必与半平凡解分支｛（d；u＊1，0）：d＞0｝交于（ d；u＊1，0），因此有如下定理：

定理2 设α＞α＊，0＜b＜，则由定理1给出的正解分支C必交半平凡解分支｛（d；u＊1，0）：d＞0｝于点

3 结语

利用分歧理论研究了具有强Allee效应的捕食－食饵模型正解的存在性．结果表明，系统（2）存在发自单重分歧点（λ；u＊2，0）的局部分支，且该分支可延拓为全局分支，最终交半平凡解分支｛（d；u，0）：d∈R＋｝于点（d；u＊1，0）．从生态学角度来看，如果捕食者的增长率控制在一定范围内，则食饵和捕食者可以共存；如果捕食者的增长率过大或太小，二者不能共存．

［1］Allee W C．Animal aggregations：A study in general sociology［M］．Chicago：University of Chicago Press，1931：35－86．

［2］Wang Jinfeng，Shi Junping，Wei Junjie．Predator－prey system with strong Allee effect in prey［J］．Journal of Mathematical Biology，2011，62：291－331．

［3］刘冠琦，史俊平，王玉文．具有强Allee影响的稳定态反应扩散方程正解的存在性［J］．哈尔滨师范大学学报：自然科学版，2006，22（3）：1－3．

［4］Wang Jinfeng，Shi Junping，Wei Junjie．Dynamics and pattern formation in a diffusive predator－prey system with strong Allee effect in prey［J］．Journal of Differential Equations，2011，251：1276－1304．

［5］叶其孝，李正元．反应扩散方程引论［M］．北京：科学出版社，1990：1－48．

［6］Ouyang Tiancheng，Shi Junping．Exact multiplicity of positive solutions for a class of semilinear problems［J］．Journal of Differential Equations，1998，146：121－156．

［7］Korman P，Li Yi，Ouyang Tiancheng．An exact multiplicity result for a class of semilinear equations［J］．Communications on Partial Differential Equations，1997，22：661－684．

［8］Smoller J，Wasserman A．Global bifurcation of steadystate solutions［J］．Journal of Differential Equations，1981，39：269－290．

［9］Gui Changfeng，Lou Yuan．Uniqueness and nonuniqueness of coexistence states in the Lotka－Volterra competition model［J］．Communications on Pure and Applied Mathematics，1994，47：1571－1594．

［10］Smoller J．Shock waves and reaction－diffusion equations［M］．New York：Spring－Verlag，1983：167－191．

［11］谢强军，李艳玲．一类捕食模型正平衡解的分支和稳定性［J］．陕西师范大学学报：自然科学版，2004，32（1）：18－20．