输水隧洞施工独立坐标系的计算方法
2013-10-29李丽华任炜辰
李丽华 任炜辰
(1、山西省水利水电勘测设计研究院 山西太原 0300242、河海大学水利水电学院 江苏南京210098)
0 引言
水利工程是经济社会发展不可替代的基础支撑,特别近年来,随着供水需求的不断增大,许多引水工程线路长、跨度大,长距离输水隧洞增多,其坐标改算与边长投影计算难度也随之增加。根据工程测量规范要求:平面控制网的坐标系统应满足测区内投影长度变形不大于2.5cm/km,对于特殊隧洞施工精度要求更高,因此必须建立能满足大型隧洞贯通要求的施工坐标系统,并进行长度变形改算。一直以来该系统的理论计算没有实现程序化,我们查阅相关资料,结合工程允许变形值,编制了输水隧洞施工坐标系的程序软件,实现了计算机程序平差计算模式,并经多个工程使用验证,精度和计算速度成倍提高。
1 独立坐标系的建立准则
为了减小高程归化与投影变形产生的影响,必须把它们控制在一个微小的范围内,使计算出来的长度在施工过程中实际利用时不需要做任何改算,从而达到精度要求,这就需要对抵偿高程面的最佳位置以及中央子午线的最佳位置进行分析。当采用抵偿高程面作投影面建立独立坐标系统时,不但要考虑测区距中央子午线的距离和水工建筑物的设计高程,还要考虑测区范围的大小以及其他实际情况。在满足精度要求的前提下,为了使测量结果一测多用,应采用国家统一带高斯平面直角坐标系,将观测结果归算至参考椭球面上。即工程测量控制网应同国家测量系统相联系;当边长的两次归算投影改正不能满足上述要求时,为保证测量结果的直接利用和计算的方便,可建立施工独立坐标系,归算测量结果的参考面根据工程设计方案选定,因此可用以下手段实现:①通过改变Hm(测区平均高程面)从而选择合适的高程参考面,将抵偿分带投影变形(称为抵偿投影面的高斯正形投影);②改变Ym从而对中央子午线作适当移动,以抵偿由高程面的边长归算到参考椭球面上的投影变形(称为任意带高斯正形投影);③通过既改变Hm(选择高程参考面),又改变Ym(移动中央子午线),来抵偿两项归算改正变形(称为具有高程抵偿面的任意带高斯正形投影)。
2 独立坐标系建立的数学模型
为了得到独立坐标系的坐标,经GPS网的约束平差后得到国家80坐标,然后将国家80坐标作椭球变换得到独立坐标系对应的椭球面坐标。
工程椭球为地方参考椭球,投影面在平均高程面上。构造地方参考椭球要满足的条件是:地方参考椭球的中心与国家参考椭球的中心重合,且使椭球的扁率e保持不变;地方椭球与国家参考椭球定向一致,没有旋转;满足上述两个条件,将国家参考椭球的长半轴膨胀使得参考椭球与当地投影面相切[1]。新椭球参数计算公式如下:

新大地坐标系的建立考虑到椭球的定向与定位不同、椭球参数的变化以及两坐标系统尺度的差异,常采用广义大地坐标微分公式[2]。
广义大地坐标微分方程可以简化为:

经过以上计算和变换,可以得到地方椭球的参数,然后由国家坐标计算得出在地方椭球上的大地坐标,最后进行高斯投影计算得到施工坐标。
3 软件编制
部分程序如下:


程序的界面见图1。

图1 程序的界面
4 工程案例
某工程线路全长约60km,其中输水隧洞长53km,针对该工程特点,选择建立独立坐标系的准则是:(1)在隧洞进口与出口之间边长每千米理论变形值不大于3mm;(2)国家坐标系统和施工坐标系统之间具有严密的转换关系;(3)对于平均边长不大于7.5km的三角形内角,施工坐标系统与国家坐标系统之间对应角度的角度变形值不大于1秒。(4)施工坐标系统方便于工程应用,采用有效的方法避免不同标段之间坐标值的误用。
用编制的软件对该项目进行了计算,部分计算结果见表1。
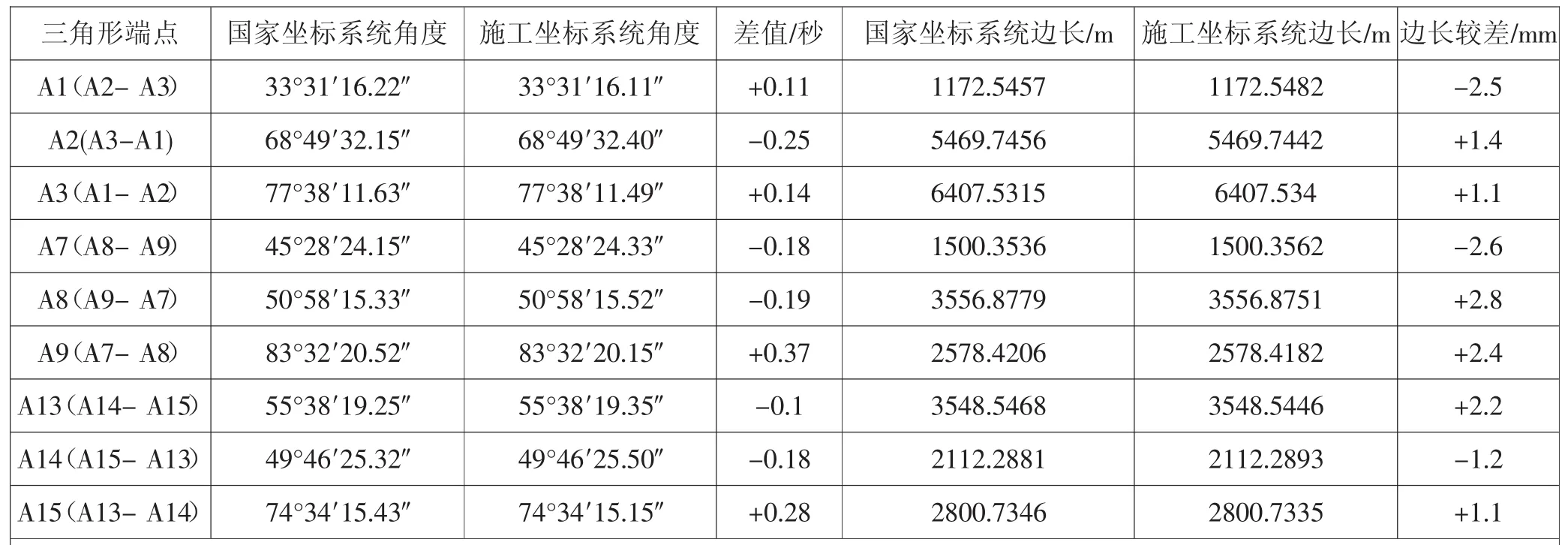
表1 计算结果
经检验计算隧道进口由高程和投影两项引起的边长每千米改正数为2.8mm,部分支洞的改正数为-2.8mm/km、-1.5mm/km、-0.3mm/km,隧洞出口改正数为2.4mm/km。对于施工坐标系统,在隧洞进口与出口之间边长每千米理论变形值不大于3mm。
5 结束语
本文通过介绍本工程输水隧洞施工控制网计算的电算化方法,讨论了工程椭球的建立方法,建立了相应的椭球模型,编制了相应的软件,结合实例计算,将国家坐标转化为施工坐标,减少或消除高差和高斯投影引起的边长变形对工程建设施工的影响,满足了施工的要求和相应的工程规范,从而保证了工程的顺利进行。
[1]李世安,刘经南,施闯.应用GPS建立区域独立坐标系中椭球变换的研究[J].武汉大学学报信息科学版,2005,30(10):889-891.
[2]徐天河,杨元喜.坐标转换模型尺度参数的假设检验[J].武汉大学学报(信息科学版),2001,26(1):70-73.
