基于中断概率的协作通信中继选择与功率分配算法

孙立悦，赵晓晖，虢明

（吉林大学 通信工程学院，吉林 长春 130012）

1 引言

随着无线通信技术及其在各个领域应用的飞速发展，现有的无线频谱资源变得空前紧张，如何提高频谱利用率和数据传输速率成为未来无线通信中亟待解决的问题。推动通信技术高速发展的MIMO（multiple-input multiple-output）技术通过空间复用和空间分集可以有效地提高数据传输速率和可靠性，但是由于其限制因素，在不同的实现过程中也有各种困难。鉴于此，协作通信技术应运而生，其基本思想是在多用户环境中，通过网络间节点资源协作的方式，有效地共享传输资源，形成虚拟天线阵列，从而获得分集增益。这项技术有诸多优点，与MIMO技术形成互补和竞争，很快成为目前国内外最新的研究热点。

最早，VAN DER MULEN和COVER等人在无线中继信道上进行了开创性的研究[1,2]，他们首次提出了由源节点、中继节点和目的节点构成的协作通信网络模型，并将系统划分为一个广播信道和一个多址信道，为协作通信的发展奠定了重要的基础。根据中继站对接收到的信息处理方式的不同，可以将协作协议分为放大转发（AF，中继将接收到的信息放大后转发）、解码转发（DF，中继将接收到的信息译码并重新编码后转发）和编码协作（CC，中继传输不再是与信源相同的信息，而是增加的冗余）等多种方式[3]。随后，LANEMAN等人研究了低复杂度的经典协作分集协议，它能够有效抵抗无线通信网络中多径效应带来的衰落损耗，并在高信噪比近似条件下分析了其中断概率的性能[3,4]。

协作通信技术涉及的研究范围很广，中继节点选择及其功率分配往往被作为重要的研究方向，在中继选择中，中断概率是其中一个重要的标准和评价方式，在此基础上再考虑实际协作通信运营环境中的一些限制条件[5~10]，而一个源节点、一个目的节点和多个中继节点的系统网络是研究热点之一[10~14]。GOMEZ-CUBA等人全面研究了无线网络的协作分集技术，提出了一个通用的理论框架[9]。WANG等人对协作MIMO信道模型现状进行深入研究，说明了尽管现有的标准化的点对点MIMO信道模型在一定程度上得到应用，但仍存在很多新的挑战[15]。ERKIP等人研究的中继选择算法需要知道链路每一跳的距离，用户协作区域的位置和大小与源节点和目的节点的位置有关，因此不适用于动态网络[5~7]。ZHAO等人在AF模式下，基于瞬时信道信息，提出一种最优中继选择方案，证明了选择一个最优中继与多中继参与协作获得的分集阶数相同[8]。随后，ANNAVAJIALA等人提出了高信噪比近似下系统中断概率表达式，比较分析了源节点与目的节点之间有无直接链路2种情况在AF/DF/DSTC 3种协议下的系统中断性能[16]。上述2种方案都是基于瞬时信道信息，需要时刻掌握系统的信道状态，并反馈给参与通信的全部节点，复杂度高，开销大。在ANNAVAJIALA等人的基础上，文献[10,11,13]研究了在AF协议下，基于中断概率的中继选择算法，给出了等功率分配条件下最优中继集合的选择算法，但实际中继节点的选择未必依据等功率条件，且由等功率条件下选择的中继节点推导出的中断概率可能会变大，不能保证系统达到最佳性能。BAI等人基于距离中继选择方案，深入研究了路径损耗，在机会中继算法的基础上提出了新的中继选择方案，但该方案不能实时精确地选择最佳中继[17]。尽管基于等功率分配 AF协作系统的中继选择的研究工作有很多，但是目前仍没有文献研究功率优化后的中继选择技术在 AF协作系统中的应用。

考虑上述问题，本文在 AF模式下，采用拉格朗日乘子法和最陡下降法，提出了一种基于信道统计特性的中继选择与功率分配算法。该算法在中继选择之前对源节点和各个中继节点进行了功率优化，然后根据当前信噪比自适应地选择最优中继集合，最后对源节点和最优中继集合进行功率再分配。该方法避免了等功率分配下选择中继节点对中断性能的影响，同时未被选择的中继节点处于空闲状态，降低了资源损耗并提升了系统寿命。仿真实验表明，在相同条件下，本算法性能是最优的。

2 系统模型

多节点协作中继网络模型如图1所示，该系统存在一个源节点S，一个目的接收节点D和n个采用放大转发方式的中继节点 Ri（ i = 1 ,… ,n ）。假设源节点和中继节点的发射功率分别为 Es和 Ei，参与转发数据的中继节点集合为 L = ｛1, 2 ,…, l ｝，分别采用均值为零的相互独立的复高斯分布随机变量 hsi，hsd和 hid表示源节点到中继节点和目的节点以及中继节点到目的节点的信道增益，它们的方差分别为各个节点之间信道是统计独立的，并且服从频率平坦衰落。在实际通信环境中，考虑到中继节点的射频设备限制，中继节点在同一频段上很难同时收发数据，因此本文采用半双工模式，即在同一频段节点不能同时收发信息。并且采用时分方式构成正交信道，即每个节点传输数据占用一个时隙，避免信道之间相互干扰。

整个协作通信过程分为 2个阶段。第一个阶段，源节点广播其需要发送的数据，被选择出来的中继节点和目的节点同时接收源节点的数据。令源节点发送的数据为x。sdz和siz分别表示相应信道上的加性高斯白噪声，它们是相互独立的均值为零、方差分别为sdZ 和siZ的复高斯随机变量。这时目的节点D和参与协作的中继节点iR接收到的数据分别为

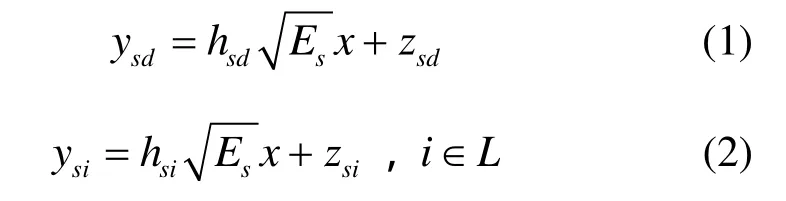
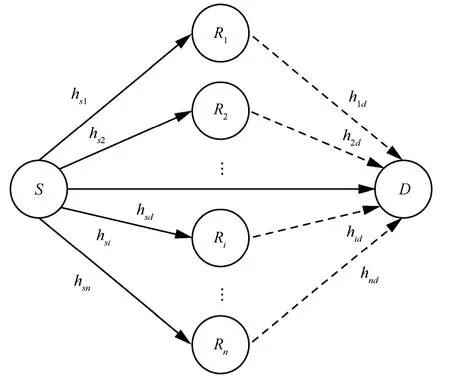
图1 多节点协作中继网络模型

第二个阶段，中继节点将接收到的数据模拟处理后放大并转发给目的节点。令参与转发数据的中继节点转发的数据为 xi=αysi，其中，α=为缩放系数[10]，则目的节点接收到来自中继节点i的数据可表示为

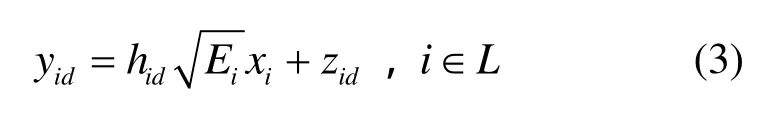
其中， zid为加性高斯白噪声，是相互独立的均值为零、方差为 Zid的复高斯随机变量。为考虑问题方便，做以下假设： Zsi= Zid= Zsd= Z0。

所有中继节点都参与协作，在AF协议下，因为数据从源节点通过n个中继节点到达目的节点共分为 n + 1个时隙，形成n个相互正交的信道，所以源节点到目的节点的链路容量可以表示为[16]

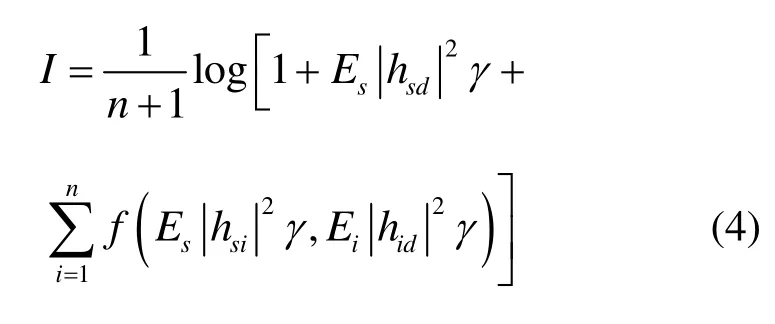
当链路容量不能满足所要求的用户速率时就会产生中断事件，这个事件发生的概率由链路的平均信噪比及其信道衰落分布模型决定。当要求速率为R时，中断概率定义为

其中， C ( n) = （ 2(n+1)R- 1 ）n+1(n + 1 )!。

3 算法描述

3.1 功率优化算法

在协作通信中，中断概率是一个重要的系统通信质量评价标准和评价方式，在此基础上再考虑实际协作通信中的一些约束条件。因此，本文研究在总功率受限条件下，找到源节点和潜在中继节点的最优功率分配因子以使中断概率最小。该问题可以用如下数学模型描述为

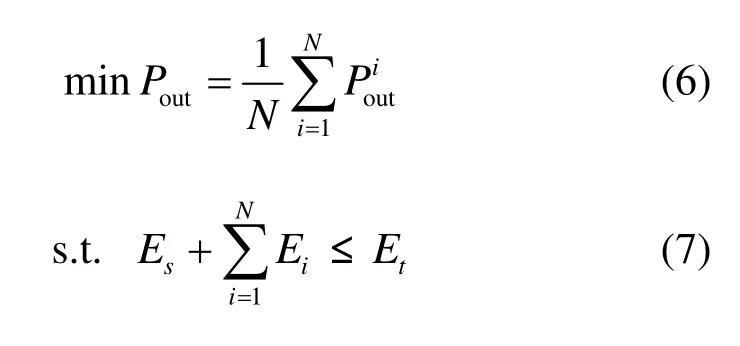
其中， Et是总的发送功率。这是一个典型的凸优化问题，可以利用经典的拉格朗日乘子法求解。

假设源节点的功率分配因子为β0，中继节点的功率分配因子为 βi, i = 1 ,… , n ，则有

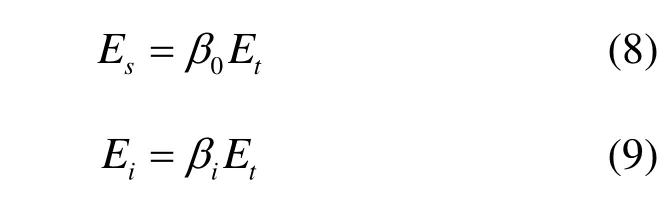
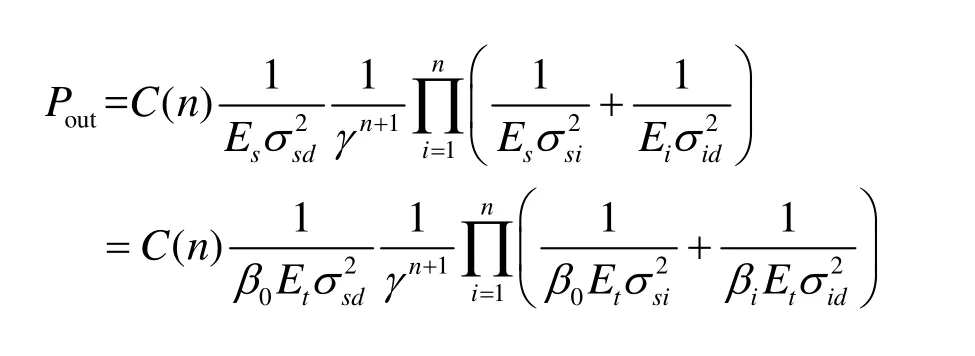
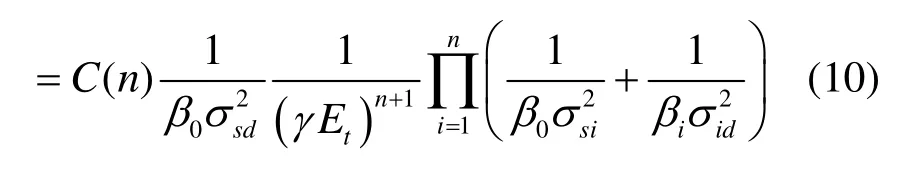
显然out0P ＞ ，将式(10)两边分别取对数，得

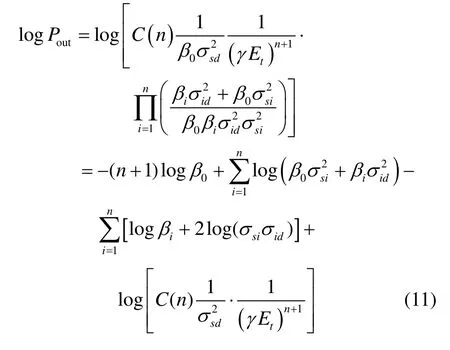
由于在通信环境确定后，上式中最后一项为常数，对优化结果无影响，可忽略。由此定义拉格朗日代价函数为

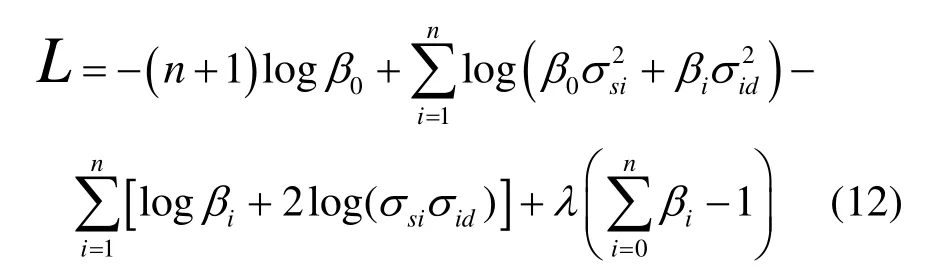
其中，λ是拉格朗日乘子。最小化代价函数，分别对β0、βi( i = 1 ,…, n )以及λ求导，并令其等于零，得

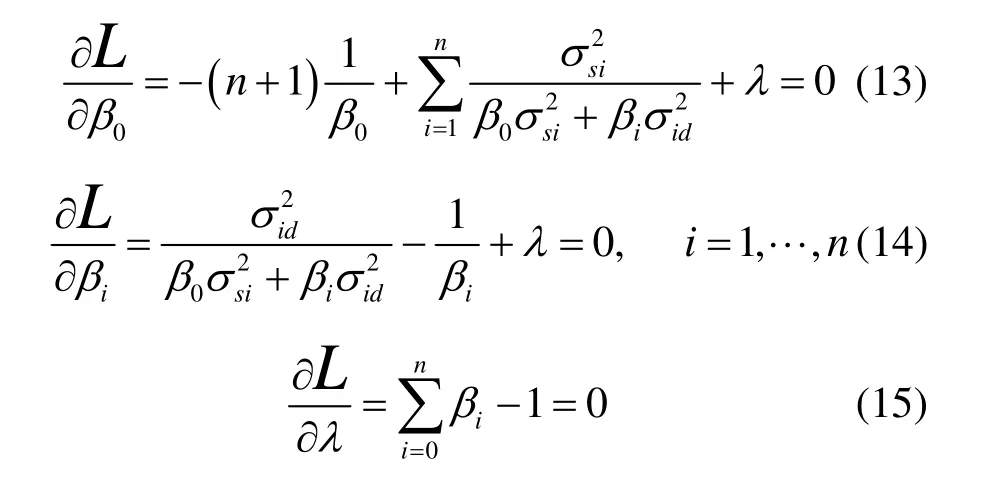
用最陡下降法求解以上三式，可得到源节点和所有潜在中继节点的功率分配因子为

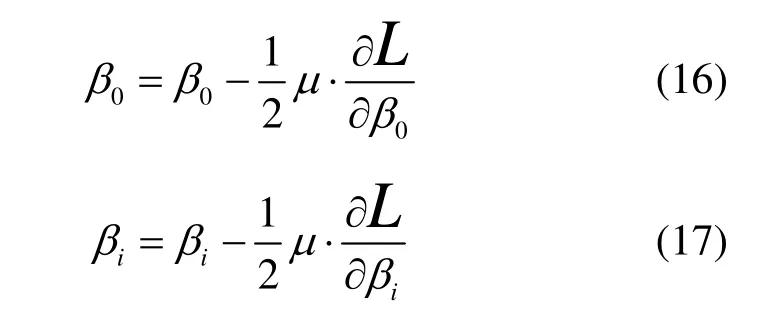
3.2 中继选择算法

在协作通信中，协作关系的形成是一个很重要的问题，涉及如何在众多潜在中继中选择合适的节点或节点集合以求给系统带来更大的增益。也就是本节要重点研究的问题。

传统的中继选择算法是枚举法（full-search algorithm），即将系统中存在的中继节点一一列举出来，再对其逐一研究，找到可能的全部节点组合，计算其功率分配之后的中断概率，通过全局搜索的方法找到最优中继节点集合。但是可能的全部节点组合共有种，其中L表示参与协作的中继节点个数，N表示通信系统中存在的全部中继节点个数。可见，当N很大时，该算法的计算复杂度非常高，运算量非常大，缺点越发明显。为了减低计算复杂度，本节给出一种低复杂度的中继选择算法，只需求得中继节点排列矩阵便可根据当前信噪比自适应获得最优中继节点集合，复杂度大大降低。

本算法基于信道统计特性进行中继选择，不需要知道大量瞬时信道信息。并且在中继选择之前对源节点和各个中继节点进行了功率优化，避免了等功率分配下选择中继节点对中断性能的影响。很明显，当中继节点集合不同时，计算出来的0β和iβ也不同。因此，将不同的中继节点集合对应的功率分配因子表示为βi,0、βi,j, j = 1,… ,i 。

从式(11)可以看出，中断概率outP 与有关。因此，定义中继节点 Ri的等效信道增益（ECG，equivalent channel gain）为

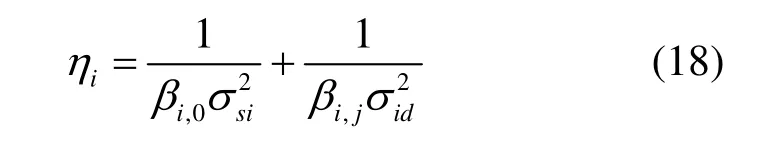
为了进行中继选择，需要得到中继节点排列矩阵，在该矩阵中，中继节点根据其等效信道增益ηi的大小进行升序排列，该矩阵可表示为 Γ =[R1, R2,… ,Rk, … ,Rn]，其中，Rk表示在潜在中继中等效信道增益第k小的那个中继节点。得到中继节点排列矩阵Γ之后，中继选择可以很快地完成，即当参与协作的中继节点数为l，则此时的中断概率为

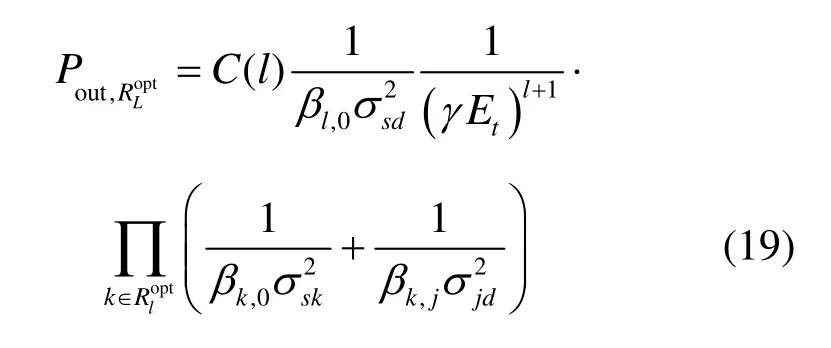
假设已得到所有中继节点的排列矩阵，当信噪比为γ时，则在n个中继节点中选择l个中继节点的最优值为

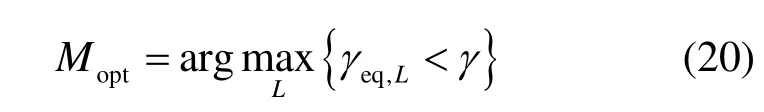
其中，

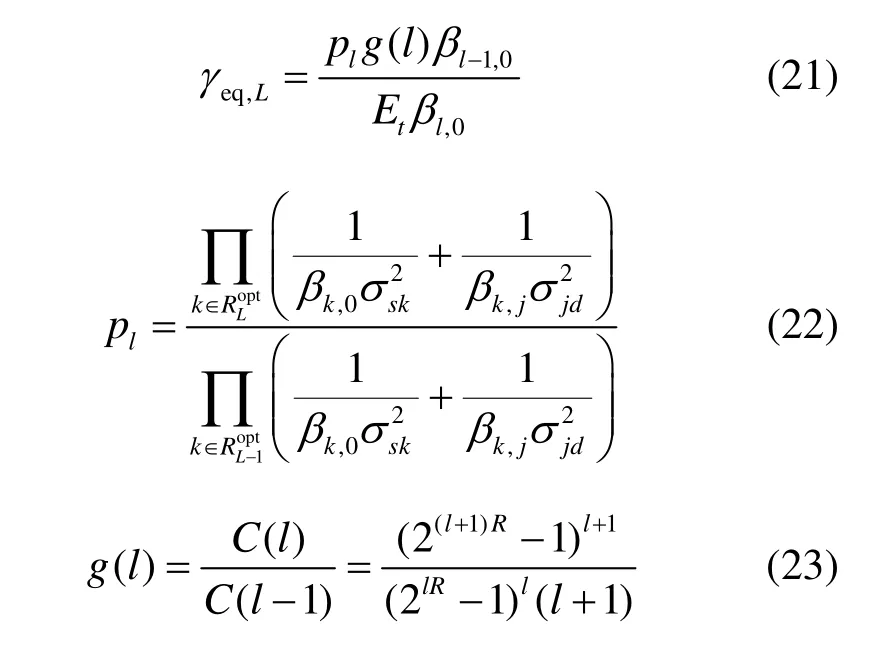
相应的最优中继节点集合为

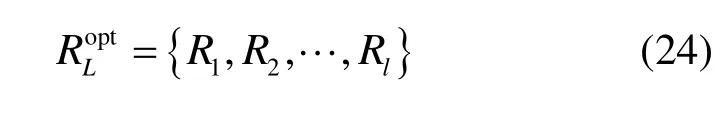
下面给出式(20)结论的证明。

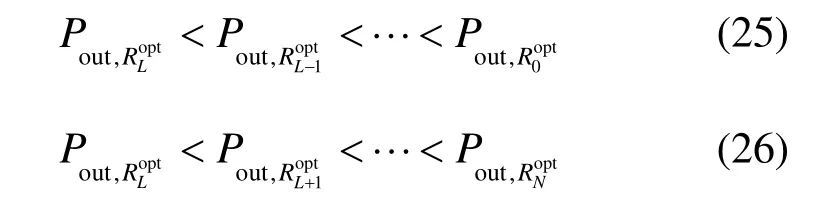
结合式(25)、式(26)和式(19)，可得

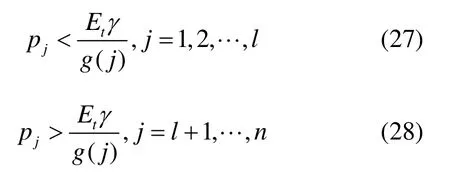
由于 ()g j和jp都是随j单调递增的函数，那么可以分别得到

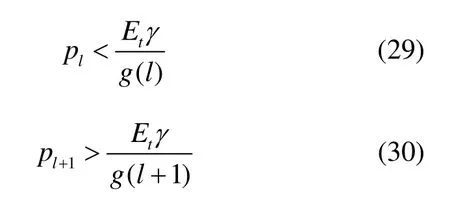
综上可得

本文算法的具体步骤如下。

1) 根据当前信道状况，对源节点和所有中继节点进行全局功率优化，求得功率分配因子βn,0、βn,j( j = 1 ,… , n )。

2) 根据式(18)计算各潜在中继节点的等效信道增益ηi，并生成中继节点排列矩阵Γ。

3) 根据式(21)计算γeq,L并与当前信噪比γ进行比较，根据式(24)找到最优的中继集合｛R1, R2,… ,Rl｝ 。

上述优化算法在完成中继选择时，只需进行 2次功率分配，设功率分配算法的复杂度为T，则PPRS算法的运算复杂度约为2T。枚举法需要进行次功率分配，枚举法的总运算复杂度约为2NT。由此可见，本文提出的算法极大地降低了运算复杂度。

4 仿真结果及分析

本节采用Monte-Carlo方法对本文所提出的算法进行性能评估。在仿真场景中，基站和用户之间共有5个中继站（ 5N= ）。仿真参数如表1所示。

表1 不同信道状况下的仿真参数值

图2给出了本文提出的算法在不同中继节点个数下系统中断概率性能曲线。图中的“SNR”表示系统当前信噪比，是上文中的“γ”。可以看出，中断概率随着信噪比的增加而降低，而且并非参与协作的中继节点数越多，系统的平均中断概率越低。已知中继节点排列矩阵中的中继节点等效信道增益按升序排列，根据图2中曲线交点可以得出以下结论：当 γ ≤ 5 .72 dB 时，选择一个中继的中断概率最小；当5.72 dB ＜ γ ≤10.73dB时，选择2个中继的中断概率最小；当10.73dB＜γ≤ 1 4.78dB时，选择3个中继的中断概率最小；当14.78dB＜γ≤17.85dB时，选择4个中继的中断概率最小；当 γ ＞ 1 7.85dB 时，选择5个中继的中断概率最小。值得注意的是，当信噪比较低时，平均中断概率大于1，曲线略有偏差，这是由于式(5)是在高信噪比下近似简化得来的缘故。

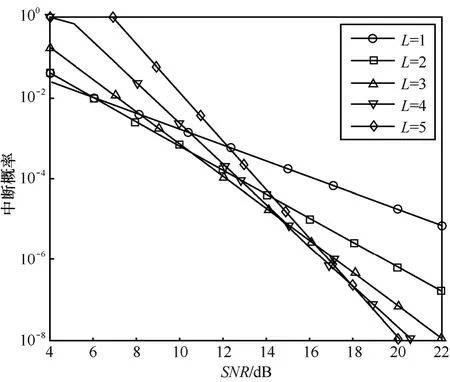
图2 本文算法在不同中继节点个数下的中断概率曲线

当通信环境确定时，根据式(20)，得到最佳中继节点数L与信噪比γ的关系曲线如图3所示。在已知当前信噪比的前提下，便很容易明确该系统的最佳中继集合。可以看出与图2中得到的分段关系结果相一致。

图4给出了在5个中继节点网络中，选择不同中继集合时( L = 1 ,2,… ,5 )，本文算法与等功率分配中继选择（EPRS, equal power allocation based relay selection）算法及基于最优功率分配的中继选择(OPRS, optimal-power-allocation-based relay selection)算法的中断概率性能曲线。本文提出的中继选择算法称之为PPRS（pre-power allocation and relay selection）算法。从仿真结果可以看出，相比于其他2种算法，本文提出的算法的中断概率始终是最低的。并且最优中继集合包含的中继节点数越少，本文算法相对于 EPRS算法的优势越显著。当 1L=时，PPRS算法比 EPRS算法平均提升了5.48 dB的性能增益；而与OPRS算法性能几乎重合，因为此时参与协作的中继较少，且2种算法选择了相同的中继节点。当 2L= 时，PPRS算法比EPRS算法平均提升了4.19 dB的性能增益；比OPRS算法有0.55 dB左右的性能改善。当 3L=时，PPRS算法比EPRS算法平均提升了2.97 dB的性能增益；比OPRS算法有0.64 dB左右的性能改善。当 4L= 时，PPRS算法比EPRS算法平均提升了1.93 dB的性能增益；比OPRS算法有0.55 dB左右的性能改善。当 5L= 时，PPRS算法比EPRS算法平均提升了1.12 dB的性能增益；而与OPRS算法接近，因为此时全部潜在中继节点都参与协作(L N= )。

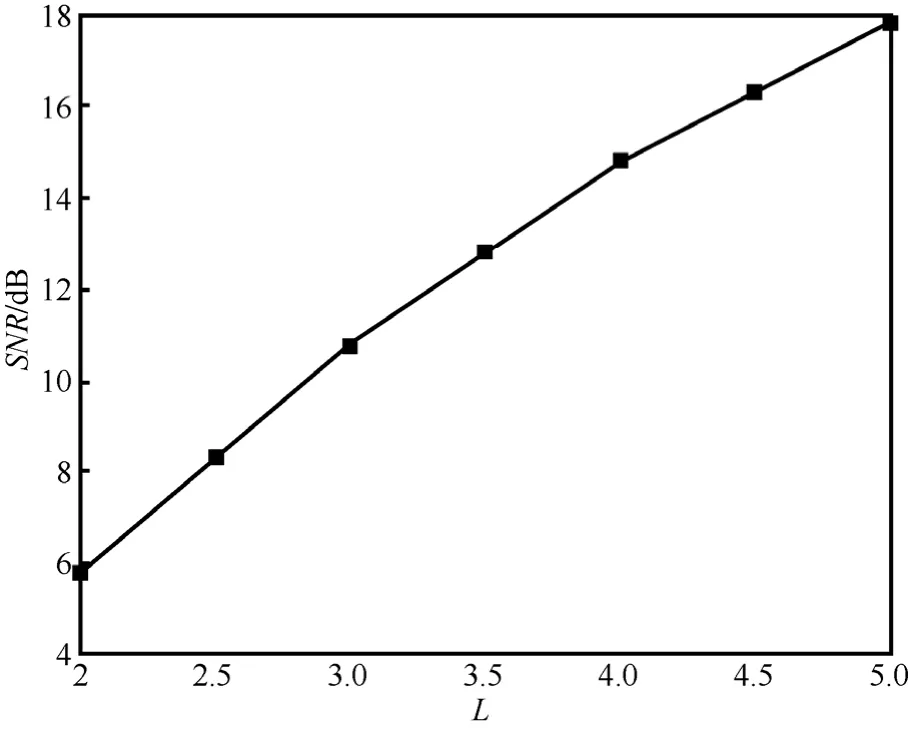
图3 不同最佳中继节点数L与信噪比γ关系曲线

图5给出了本文提出的PPRS算法和2种传统的中继选择算法的中断概率性能曲线。其中，SAF算法是选择一个最好的中继节点参与通信；AAF算法是全部潜在的中继节点都参与通信。可以看出，在任意信噪比下，本文算法均优于其他2种算法，可以大幅降低中断概率。

5 结束语

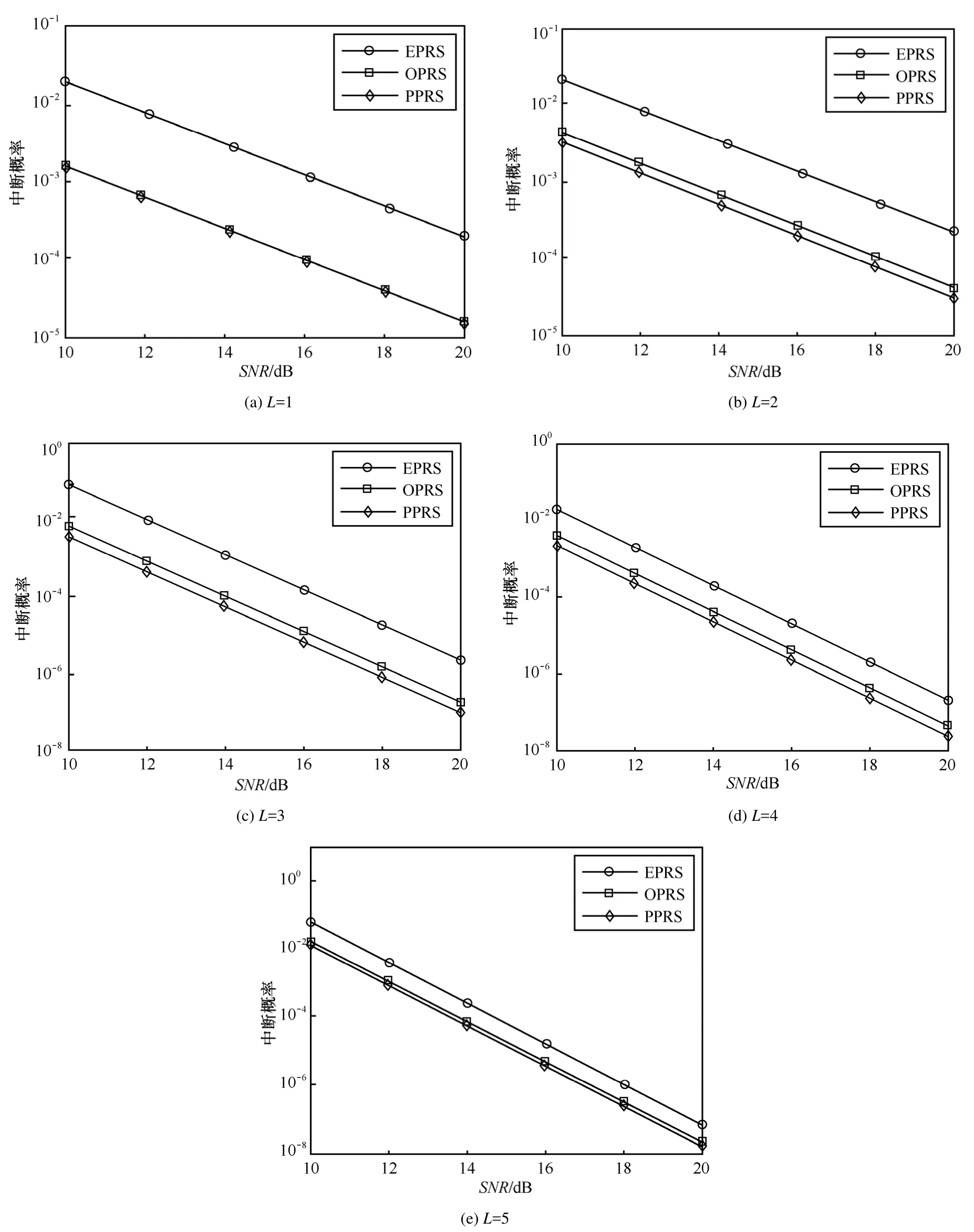
图4 在有5个中继的网络中，选择不同中继集合时3种算法的中断概率曲线

本文以一个基站、一个用户和 5个中继站为通信模型，在AF模式下，结合拉格朗日乘子法和最陡下降法，提出了一种基于最小中断概率的中继选择与功率分配算法——PPRS算法。相对于枚举法、EPRS和OPRS算法，本文提出的PPRS算法不需要知道大量瞬时信道信息、不需要系统在等功率条件下进行中继选择，只需求得中继节点排列矩阵便可根据当前信噪比自适应获得最优中继节点集合。仿真实验分析了中继节点个数与信噪比、系统平均中断概率之间的关系。多组仿真结果表明，在相同条件下，PPRS算法的中断性能始终优于文中提到的其他算法，可以有效降低中断概率，提升系统性能和功率效率。

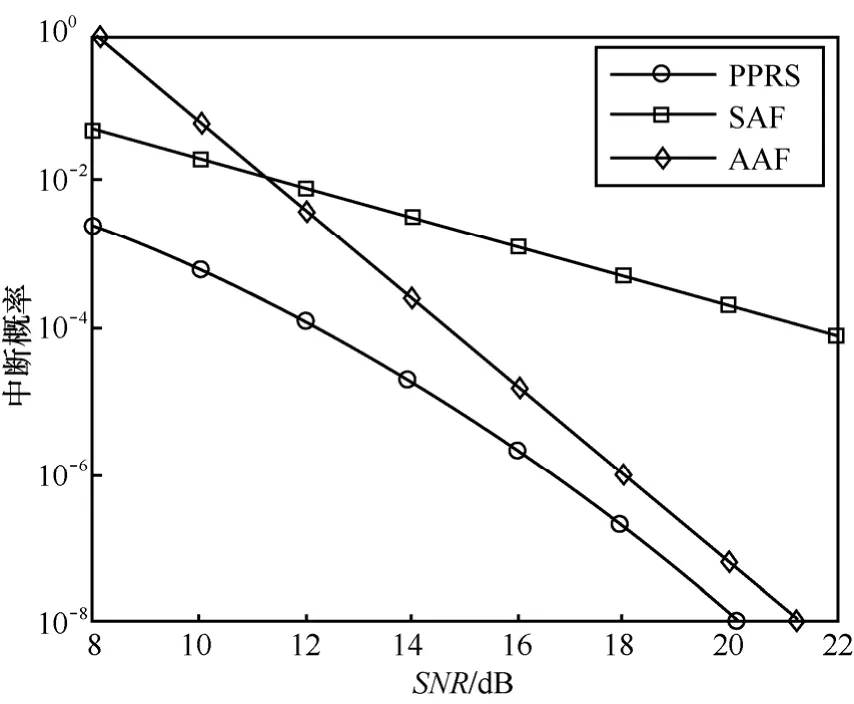
图5 PPRS算法与SAF及AAF算法中断概率曲线

[1] VAN DER MEULEN E C. Three-terminal communication channels[J].Advances in Applied Probability, 1971, 3(1):120-154.

[2] COVER T M, GAMAL A E L. Capacity theorems for the relay channel[J]. IEEE Transactions on Information Theory, 1979, 25(5): 572-584.

[3] LANEMAN J N, WORNELL G W. Distributed space-time coded protocols for exploiting cooperative diversity in wireless networks[J].IEEE Transactions on Information Theory, 2003, 49(10):2415-2425.

[4] LANEMAN J N, TSE D N C, WORNELL G W. Cooperative diversity in wireless networks: efficient protocols and outage behavior[J]. IEEE Transactions on Information Theory, 2004, 50(12):3062-3080.

[5] LIN Z N, ERKIP E, STEFANOV A. Cooperative regions and partner choice in coded cooperative systems[J]. IEEE Transactions on Communications, 2006, 54(7):1323-1334.

[6] LIN Z N, ERKIP E. Relay search algorithms for coded cooperative systems[A]. IEEE Global Telecommunications Conference (GLOBECOM)[C]. Atlanta, USA, 2005. 1314-1319.

[7] LIN Z N, ERKIP E, STEFANOV A. Cooperative regions for coded cooperative systems[A]. IEEE Global Telecommunications Conference (GLOBECOM)[C]. Dallas, Texas, 2004. 21-25.

[8] ZHAO Y, ADVE R, LIM T J. Improving amplify-and-forward relay networks: optimal power allocation versus selection [J]. IEEE Transactions on Wireless Communications, 2007, 6(8):3114-3123.

[9] GOMEZ-CUBA F, ASOREY-CACHEDA R, GONZALEZ-CASTANO F J. A survey on cooperative diversity for wireless networks[J]. IEEE Communications Surveys and Tutorials, 2012, 14(3):822-835.

[10] 吴素闻，王振，朱近康. 基于信道特性的中继选择协作通信方法研究[J]. 中国科学技术大学学报, 2009, 39(11): 1136-1140..WU S W, WANG Z, ZHU J K. Study of statistical channel knowledge-based cooperative relay selection[J]. Journal of University of Science and Technology of China, 2009, 39(11): 1136-1140.

[11] 刘顺兰，徐光建. 改进的多用户协作通信系统中继选择策略[J]. 计算机工程, 2012, 38(6):101-103.LIU S l, XU G J. Improved relay selection strategy of multi-user cooperative communication system[J]. Computer Engineering, 2012, 38(6):101-103.

[12] CAI R W, SUN E C, ZHANG Y H. An efficient cooperative relay selection scheme for SC-FDMA systems[A]. IEEE International Conference on Systems and Informatics (ICSAI)[C]. Yantai, China, 2012.1422-1425.

[13] 孙琳，马社祥. 基于误码率的快速中继选择算法[J]. 计算机应用,2011, 31(3):613-616.SUN L, MA S X. Fast relay selection algorithm based on symbol error probability[J]. Journal of Computer Applications, 2011, 31(3):613-616.

[14] GHASEMI H, FALAHATI A. Employing relay ordering in incremental amplify and forward relaying technique to improve outage probability[A]. Telecommunications Forum (TELFOR)[C]. Belgrade,Serbia, 2011.529-532.

[15] WANG C X, HONG X M, GE X H, et al. Cooperative MIMO channel models: a survey[J]. IEEE Communications Magazine, 2010, 48(2):80-87.

[16] ANNAVAJJALA R, COSMAN P C, MILSTEIN L B. Statistical channel knowledge-based optimum power allocation for relaying protocols in the high SNR regime[J]. IEEE Journal on Selected Areas in Communications, 2007, 25(2): 292-305.

[17] BAI Z Q, XU Y Q, YUAN D F, et al. Performance analysis of cooperative MIMO system with relay selection and power allocation[A].IEEE International Conference on Communication(IEEE ICC)[C].Nanjing, China, 2010. l-5.