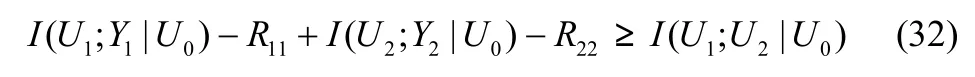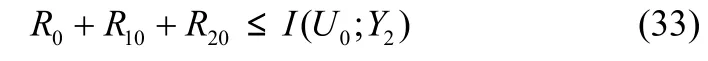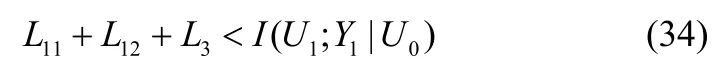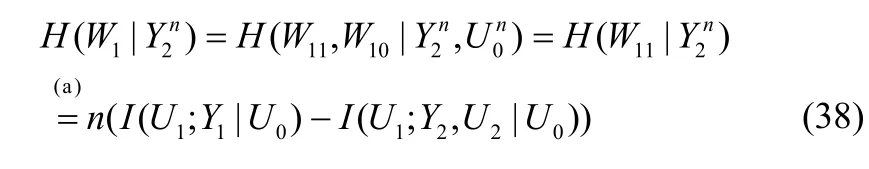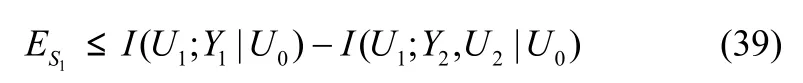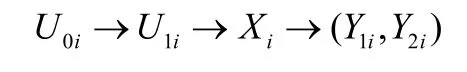基于分离信源信道码的相关信源在有噪广播信道下的可靠和安全传输

郎非，王保云,2，邓志祥

（1. 南京邮电大学 通信与信息工程学院, 江苏 南京 210003; 2. 东南大学 移动通信国家重点实验室, 江苏 南京 210096）

1 引言

传统技术实现安全保密通信是通过对明文加密来实现的。收发双方会共享一个密钥，而窃听者是不知道密钥的。这种传统加密系统面临如下问题[1]：理论上无线网络中的窃听者可以拦截任何信息，包括密钥本身；具有主动攻击特性的窃听者能够干扰合法用户之间的信息传输，使得传输质量下降；复杂网络的密钥管理分配非常困难。1948年，香农开创性地借助信息论(information theory)证明得到了一个惊人的结论：如果密钥的长度不小于明文的长度，则可实现绝对保密(perfect secrecy)。之后Wyner、Csiszár和 Körner等人[2]在没有使用密钥的前提下，证明了在窃听信道或广播信道(BC)下安全通信是可能的。基于上述先驱们的工作，形成了信息理论安全(information-theoretic security)最基本的理论。采用这种方法可以从本质上克服传统加密系统的上述缺陷，并且即使窃听者具有无限的计算资源，其安全容量也不会受到任何影响。近些年来，随着无线终端设备的普遍使用，开放的无线媒介易被非法用户侵入特质，使得无线通信安全问题被日益关注。2008年之后，越来越多的信息理论学者开始重新关注信息理论安全这一研究方向[3～10]。

基于信息理论方法实现信息安全传输的基本思想：由于信道噪声以及衰落引起信道特性的波动，使得物理层信道产生固有的随机性，利用合法接收者与窃听者所接入信道的随机性不同来实现合法用户之间信息或部分信息的安全传输。例如，信息的发送者可以有意地在原有信息的基础上增加随机信息，在保证合法用户接收信息不受影响的同时，能够阻止窃听者截获有效信息。Csiszár和 Körner[2]早期研究的广播信道只含1个公共消息和1个保密消息。近些年来，Liu等人[9]率先对含有2个保密消息的广播信道进行研究，并给出了安全容量区域的内界和外界。紧接着，Xu等人[10]对于这一模型进一步推广，给出了含有2个保密消息和1个公共消息的广播信道的速率——疑义度区域的内界和外界。

相关信源传输问题最早起源于无噪网络，有2个著名的分布式信源编码的例子。1)相关信源的分离编码，即著名的Slepian-Wolf编码[11]。这里的分离编码指相关信源经过压缩映射为2个消息集合，再分别经过两路无噪信道到达同一接收端。该编码方案得到一个令人惊讶的结果：当两路信道所能承载的码率不小于2个信源的联合熵时，则在接收端能够同时无损恢复 2个信源。2)Gray-Wyner系统[12]，该模型对Slepian-Wolf模型进行了推广，双信源经过3路无噪信道到达2个接收端。其中一路为公共信道，能同时到达2个接收端，其余两路为私人信道，分别到达2个不同的接收端。Gray和Wyner最先给出该模型系统的可达速率区域，并证明了当公共信道能够被最大限度地使用时，可以得到最优码。近期针对Gray-Wyner系统，Timo等人[13]给出当接收端有边信息时信源码率的内界和外界，Kamath等人[14]则对该系统的Gács-Körner公共信息对偶性质进行了研究；Tandon等人[3]将这一问题扩展到N个接收用户，并考虑不同用户之间的信息保密。

相关信源在有噪广播信道下传输的问题由Han和Coast[15]首先提出，Tuncel在2006年将Slepian-Wolf码扩展到有噪广播信道，他们均使用“联合信源信道编码”得到可达界[16]。在这之后其他人[17～22]所提出的编码方案也都是基于联合编码，好像从一开始就没有考虑使用“分离信源信道编码”。这主要因为“香农信源信道分离定理”[23]揭示了对于多用户信道，信源与信道分开独立进行编码在很多情况下得不到最优解。而联合编码将传统的信源编码器与信道编码器整合为一个编码器，直接将信源映射为码字进行发送，不再有信源映射为消息、消息再映射为码字这样“分离”的2个过程。对于多址信道(MAC)，联合编码可以利用不同接入节点之间的信源相关性提高节点之间的协作通信能力。对于分离编码，由于消息和码字彼此是独立的，这反而浪费了信源相关性这一特质，使得编码效率降低。对于广播信道，只要不涉及节点之间的协作，似乎使用分离编码没有那么糟糕。但是作者仍然注意到联合编码在整合信源和信道的统计分布特性方面非常方便。

本文研究离散无记忆的2个相关信源在有噪广播信道下可靠和安全传输的问题，如图1所示，这一问题相当于对前面有关信道安全、分布式信源编码和信源信道编码等问题进行了扩展。本文仍然使用传统的分离信源信道编码策略，并结合叠加码[23]、double binning[9]和安全速率划分[10]等技术，使得传输的可靠性与安全性得到保证。对于可靠性来说，通过引入 Gray-Wyner系统，明确相关信源中不同信息种类的概率关系，划分一类公共消息 M0和二类私人消息M1和M2，如图2所示。通过优化三类信息的概率分布关系，使得信源编码与信道编码的2个过程在结合之后能够得到一个比较高效的编码。对于安全性来说，首先，通过引入辅助变量V调整信源输出的概率关系，使得消息M0、M1和M2三者之间相互独立，这能够有效地防止不同消息之间的信息泄露；其次，分离编码本身能够做到消息和发送码字独立，这使得信道本身的安全容量不会受到信源相关性的影响而降低，这也是分离编码相比较联合编码的优势。

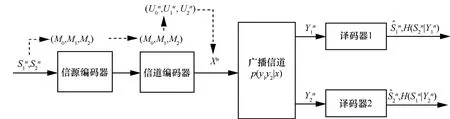
图1 分离信源信道编码的广播信道模型

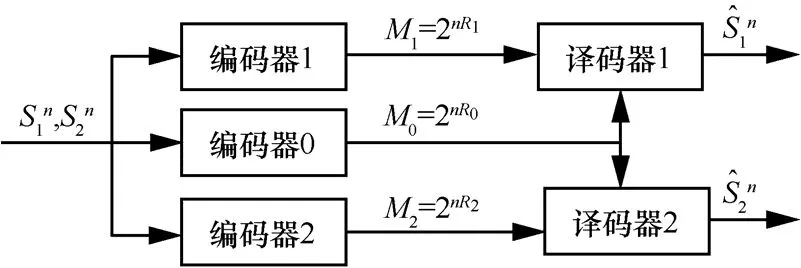
图2 Gray-Wyner 信源编译码系统

基于上述思想，本文得到了如下结论：1)相关信源在一般广播信道(general BC)下可靠和安全传输的充分条件；2)当相关信源的公共信息为二者互信息时，可获得最佳的压缩传输效率，并在一定条件下传输可做到部分绝对保密；3)退化信源集(degraded source set)在一般广播信道下可靠和安全传输的充分必要条件；4)相关信源在 more capable广播信道下可靠和安全传输的充分必要条件。以上4条结论及其部分证明在本文的第3节中进行表述，其中，结论1)的充分性证明和结论3)的必要性证明分别在附录A和附录B中进行表述。

2 基本定义和相关工作

本文符号标记规则：斜体大写字母表示随机变量，如X；斜体小写字母表示随机变量的一个实例，如x；Xn和xn表示分组长度为n的随机变量序列及其实例；用于表示 ( X ,X ,… ,X )，其中，第

1i+11i+21j一个下标“1”标识变量的名称，如X1, X2等，i和j指单个变量在变量序列中的序号；表示 ( X ,

11X12, … ,X1i)，变量实例写法亦如此；随机变量X的取值集合称为字母集，用X表示。随机变量之间的Markov关系p(x)p(x|y)p(z|y)的简化表示为X→Y→Z，可以推出X←Y←Z也成立，也可以用合并方式表达X－Y－Z。本文使用ε, ε′＞0专门来表示一个小的固定值，且ε′＜ε。使用δ( ε)＞0表示ε的函数，并当ε→0时，δ (ε)→0。εn≥0为n的函数，当n→∞ ，εn→0。

2.1 问题定义

首先给出通信模型的基本定义，分为信源和信道两部分。

Gray-Wyner系统如图 2所示，由六元组(S1, S2,fGW,M0, M1, M2)来表示。 ( S1, S2)指信源字母集， (M0, M1,M2)是消息字母集。双信源经过三元编码器组 fGW映射输出3个消息。

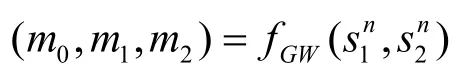
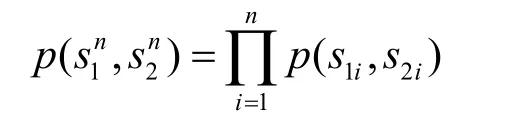
(w0, w1, w2) ∈ (W0, W1, W2) 。一般来说信道消息彼此要求独立，而对于信源消息没有这个要求。

广播信道由七元组 ( X , p, Y1, Y2, f,ψ1, ψ2)来表示，X是信道输入字母集，Y1和Y2是信道输出字母集，p是广播信道的转移概率p(y1,y2|x)，f为信道编码映射函数，Ψ1和Ψ2为2个译码映射函数。假设信道是离散无记忆的。

定义1 当发送信源为 ( sn, sn)时，分组长度为n

12的序列的译码错误概率定义为

由定义2还可以引出如下新的定义。

1) 保密信息容量： CS1= m ax ES1， CS2= m ax ES2。

2) 绝对保密： CS1= H ( S1)， CS2= H ( S2)。

3) 部分绝对保密： CS1=H( S1|S2)， CS2=H( S2|S1)。

定义3 信源(S1, S2)被允许经过广播信道传输需满足如下条件，当码字长度n足够大时，

满足这样条件的信源集合被称为允许信源区域(admission source region)。这是满足一定可靠性水平ε和安全性水平ES1ES2的信源对(S1,S2)可达区域，通常有一组不等式来进行限定。定义 3对 Han和Costa的定义[15]进行了扩展，增加对信源安全的限制。允许信源区域由不等式组来界定，它们可以理解为可靠和安全传输的限制条件。

定义4 存在一个满足某一限定条件的信源信道码序列，使得相关信源能够可靠且安全地在广播信道中传输，则称该限定条件为充分条件，亦称允许信源区域内界；反之，任何满足可靠且安全传输的信源信道码序列都必须满足某一限定条件，称该限定条件为必要条件，亦称允许信源区域外界。当内界等于外界时，则称该条件为充分必要条件，亦称最优限制条件，此时不等式所界定的区域为最优允许信源区域，对应的码序列为最优码。

2.2 证明使用的相关引理

本节给出联合典型序列的概念和证明要使用到的相关引理，详细内容可参考文献[11,23,24]。

联合典型序列：令 N ( a, b| xn, yn)标识(a,b) 在序列对(x1,y1), (x2,y2),…,(xn,yn)中出现的次数。联合概率分布p(x,y)的联合典型集可表示为

其中，(xn,yn)为联合典型集中的联合典型序列，并能得到

引理2 假设

Xn～ p( xn|un)和 (un, yn) ∈ T(n)(U Y)，

ε′

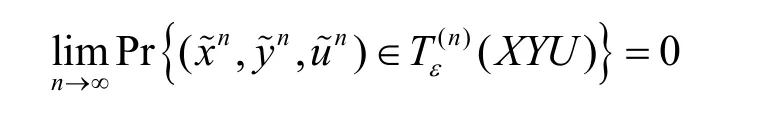
当且仅当 R ＜ I( X; Y| U ) - δ ( ε)。

引理3 （费诺不等式） 离散无记忆信道的码书为C，且输入消息W服从集合｛1,2,…,2nR}上的均匀分布，则有是在信道接收端对W的估计， P(n)= P r(W ≠ W ˆ)。

e

引理 4 （数据处理不等式）若 X－Y－Z构成Markov 链，则有 I(X;Y)≥I(X;Z) 或 I(Z;Y)≥I(X;Z)。

3 主要贡献

3.1节中给出本文的主定理，即定理1，其是针对一般的信源与信道条件而得到的可靠和安全传输限制条件。后面 3个小节（3.2节、3.3节、3.4节）分别考虑几种特殊情况，其中，定理2是在考虑双信源的公共信息满足一定条件下得到的一个较优结果；定理3则考虑双信源是退化信源集时得到的一个最优结果；定理4是在考虑广播信道满足“more capable”条件下得到的一个最优结果。

3.1 相关信源可靠性和安全性传输的限制条件

定理1 辅助变量(V, U0, U1, U2)∈V×U0×U1×U2满足如下Markov链

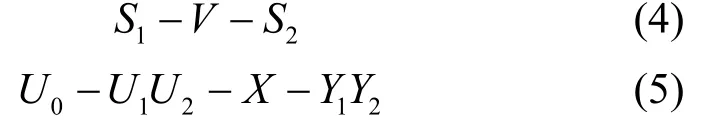
信源(S1,S2)经过广播信道 p(y1,y2|x)，到达各自的接收端。系统满足可靠性和安全性传输的充分条件为

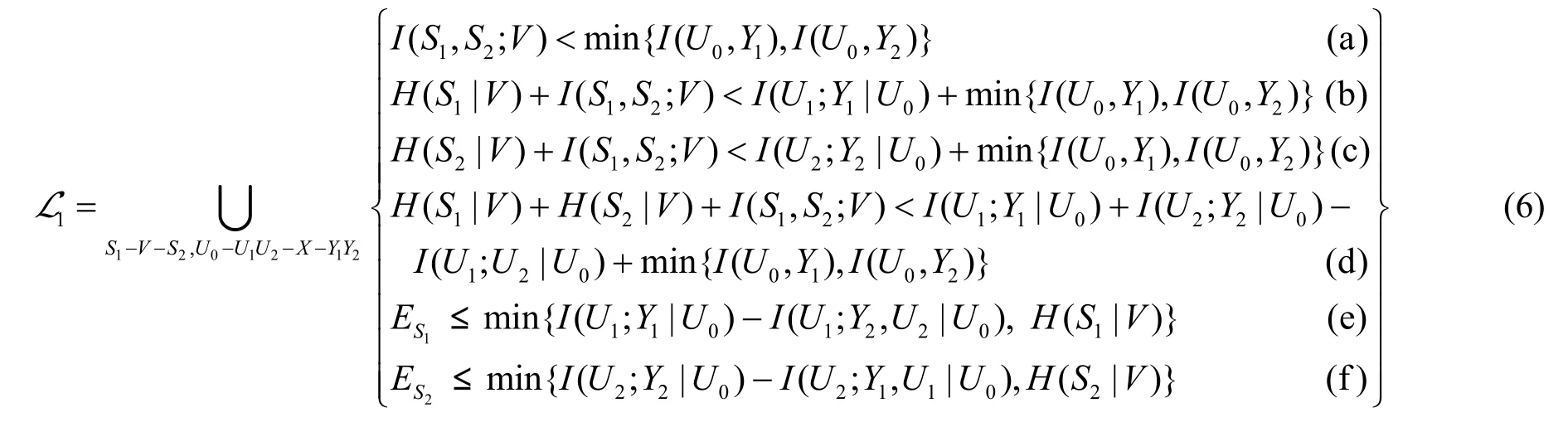
L1即为充分条件所界定的可达允许信源区域。其中， ES1和 ES2表示允许信源区域的疑义度（安全性）水平，以 ES1为例，考虑以下2种情况：

1) 当 S1满足 H ( S1| V ) ＞ I( U1; Y1| U0)- I( U1; Y2,U2|U0)时，则疑义度水平 ES1恒等于信道安全容量CS=I( U1; Y1| U0) - I( U1; Y2, U2|U0)这一固定值；

2) 当 S1满足 H ( S1|S2) ≤ I( U1; Y1| U0) - I( U1;Y2|U0)时，则 ES1等于H(S1|V)。

从编码设计的角度，期望允许信源区域尽可能大，即不等式(6a)～(6d)左半部信源压缩界越小越好；而右半部信道可达速率界越大越好。允许信源区域的计算结果，取值于所有符合Markov链式(4)和式(5)的联合概率分布。两条 Markov链式(4)和式(5)彼此是独立的，即将信源与信道概率分布完全独立开来，这是由分离编码设计决定的。辅助变量V与S1,S2均相关，可看作是S1和S2的公共信息。U0代表信道传输的公共信息，而U1和U2代表信道传输的私密信息，有一定的保密性要求。

证明 见附录A。

对于定理1考虑一种简化情况，即信道“无噪”，并且在没有安全性约束的条件下定理 1会退化为Gray-Wyner界[12]。

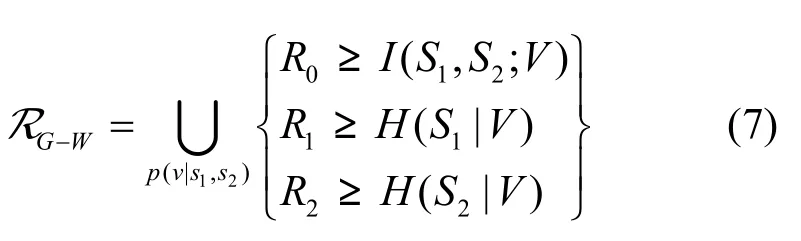
式(7)中假设三路无噪信道（一路公共信道和二路私人信道）所能承载的码率分别为R0、R1、R2。

3.2 公共信息对信源压缩率和疑义度的影响

在Gray-Wyner系统中（如式(7)所示），代表公共信息的辅助变量V的概率分布特性不仅会影响双信源的压缩效率，而且会影响疑义度水平（如式(6e)、式(6f)所示)。根据定理 1 和 Gray-Wyner界（式(7)）得到如下3个推论，其中，满足推论1可以得到双信源的最佳压缩率，而满足推论2和推论3条件的公共码率R0可以得到次优的保密条件，基于此3个推论得到定理2。

推论1 Gray-Wyner系统(R0,R1,R2)∈RG-W，当满足S1－V－S2时，则 R0+ R1+ R2= H( S1, S2)。

证明 显然联合熵 H ( S1, S2)代表信源 S1和 S2的最佳压缩率。

由Gray-Wyner系统定义式(7)可得

又因为S1-V-S2，则有

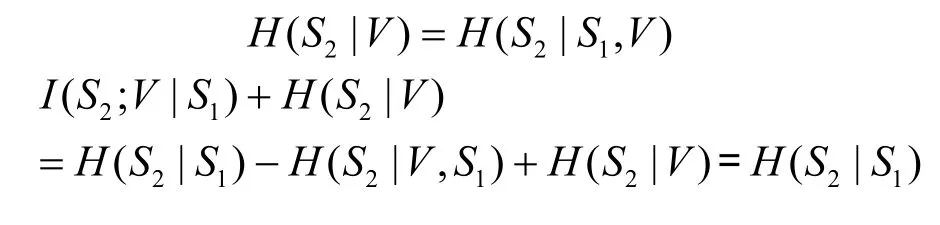
所以有

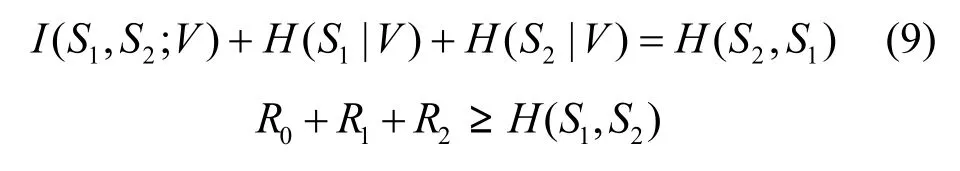
当不等式取等号时，即得推论1。

推论2 Gray-Wyner系统(R0,R1,R2)∈RG-W，最大公共信息速率 R0满足 2R0+R1+R2=H(S1)+H(S2)，则 max R0=I(S1;S2)。

证明 由Gray-Wyner系统定义式(7)可得2R0+ R1+R2

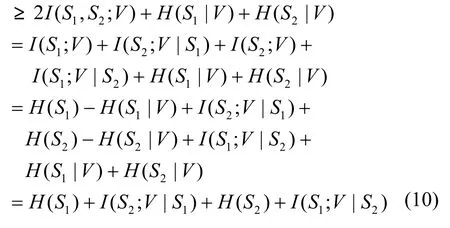
令 I ( S2; V| S1) = 0 和 I ( S1; V | S2) = 0 ，当且仅当S1、S2、V同时满足Markov链

并由此会有如下不等式和等式。

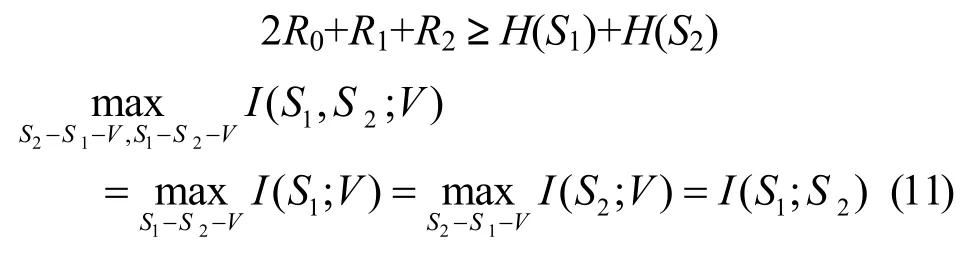
以上过程均满足可逆性，即存在一反向结论：当(R0,R1,R2)∈RG-W且I(S1;S2)=R0时，有

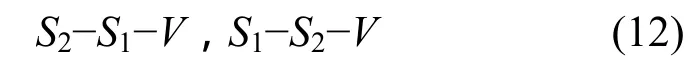
进一步会得到

推论3 当定理1中的S1和S2的公共信息等于两者之间的互信息，并满足

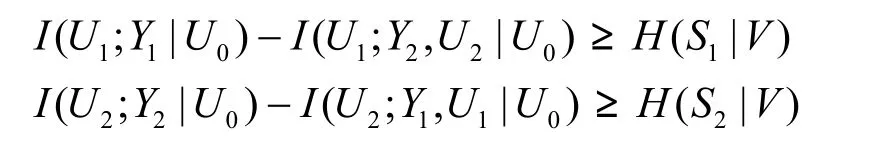
则相关信源传输可达到部分绝对保密，即

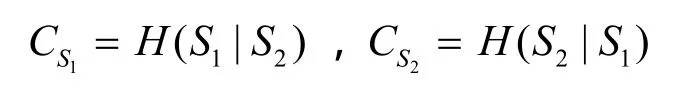
证明 公共信息的大小会直接影响疑义度，显然由于公共信息可被任意接收用户所识别，而公共信息又与信源 S1和 S2相关，会引发信息泄露。所以从安全性的角度考虑，本文期望公共信息尽量地小，同时还要满足Markov约束条件S1-V-S2。后者约束条件保证了接收用户在得到公共信息之后，不能够利用已知信源（如S1）信息再获取不同于公共信息的有关另一信源（如S2）的信息。从安全性的角度来看，推论3所设置的约束条件是在定理1的基础上，尽可能地减少了公共信息量，从而获得更高水平的安全性。

根据定理1和推论2，得到Markov链

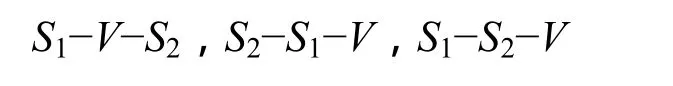
再根据数据处理不等式，由S1-V-S2得到

由S2-S1-V得到

由S1-S2-V得到

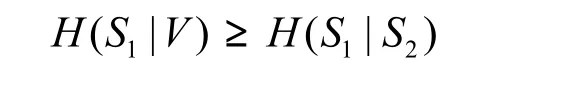
故有

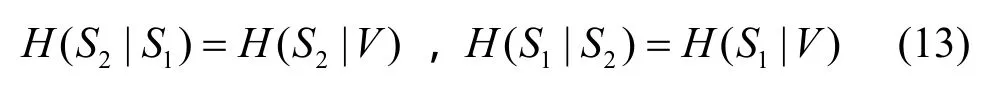
定理2 在定理1中，当I(S1,S2;V)=I(S1;S2)时，则L1退化为L2。

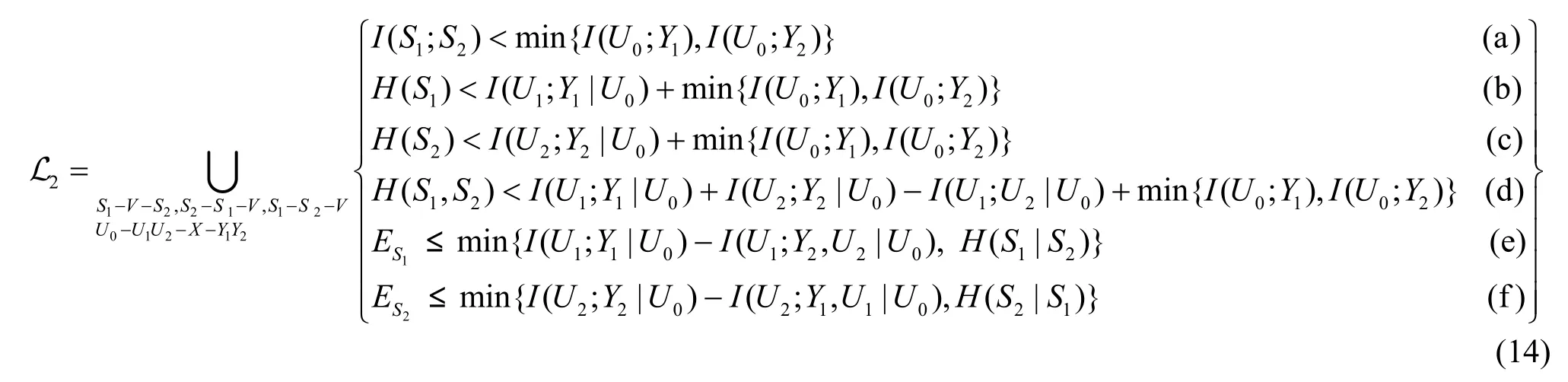
证明

根据推论1～推论3，有如下结论

同理可得

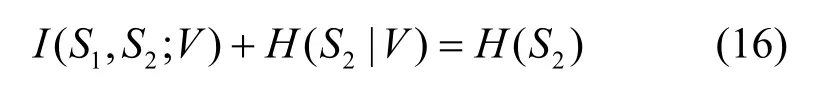
综合式(9)、式(13)、式(15)、式(16)，得到不等式组式(14)，定理2得证。

相比较定理1，定理2得到允许信源区域L2的信源压缩界（不等式(14a)～不等式(14d)的左半部）是最优的，并且满足推论3中相关信源传输可达到部分绝对保密的条件。

3.3 退化信源集

定理3 信源S1和S2经广播信道发送给译码器1，同时只将 S1发送给译码器 2，称该系统为具有退化信源集[17]的广播信道，满足可靠性和安全性传输的充分必要条件为

证明 见附录B。

充分必要条件所确定的区域L3为最优允许信源区域，此时分离信源信道编码为最优码。当满足I(U1;Y1|U0)-I(U1;Y2|U0)≥H(S1|S2)时，此时系统可以做到对S1“部分绝对保密”。

当不考虑信源编码仅对信道来说，系统简化为具有一个公共消息W0和一个秘密消息W1的广播信道，W0和W1的熵分别为nH(S2)和nH(S2|S1)。L3退化为Csiszár和Körner的容量——疑义度界[2]。

3.4 More capable广播信道

定理4 对于广播信道p(y1,y2|x)，假设Y1的能力大于Y2的能力，即对于所有输入分布p(x)，都有I(X;Y1)≥I(X;Y2)，则称该信道为more capable广播信道[23]，相关信源 S1和 S2在该信道上满足可靠性和安全性传输的充分必要条件：

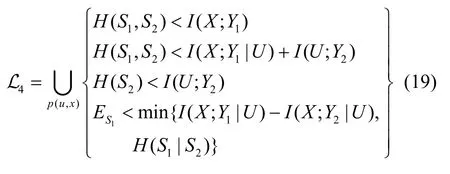
证明

首先给出定理3的另外一种等价表达形式。

注释 L'3仍是充分必要条件，并且在不考虑安全的情况下，用(R0,R1)替换不等式组(20a)～不等式组(20c)的左半部的压缩界，则L'3退化为具有退化消息集或more capable广播信道的一个容量界[23]。这里由于篇幅限制，不再对L'3进行证明。

充分性 将不等组(20)中 U 替换 U0，X替换U1，即得不等式组(19)。

必要性 只需证明不等组(20)中的信道外界（不等式右侧）都不大于不等式组(19)右侧的互信息表达式，则L4也是一个外界。

当满足L'3中 U0→ U1→ X → ( Y1; Y2)和定理4中I( X; Y1) ＞ I( X; Y2)的条件时，则有

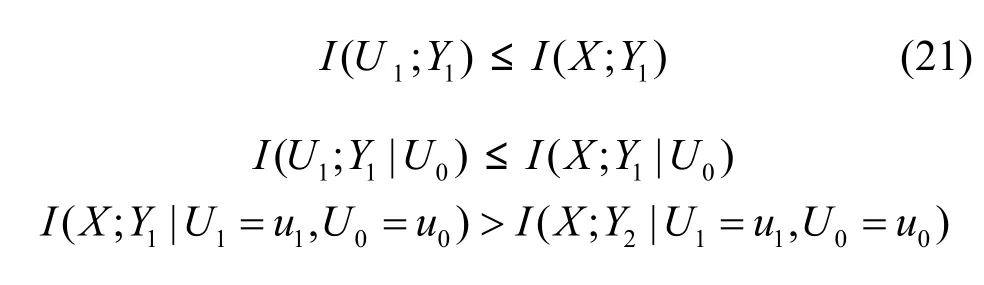
进一步会有

进一步考虑疑义度限制条件

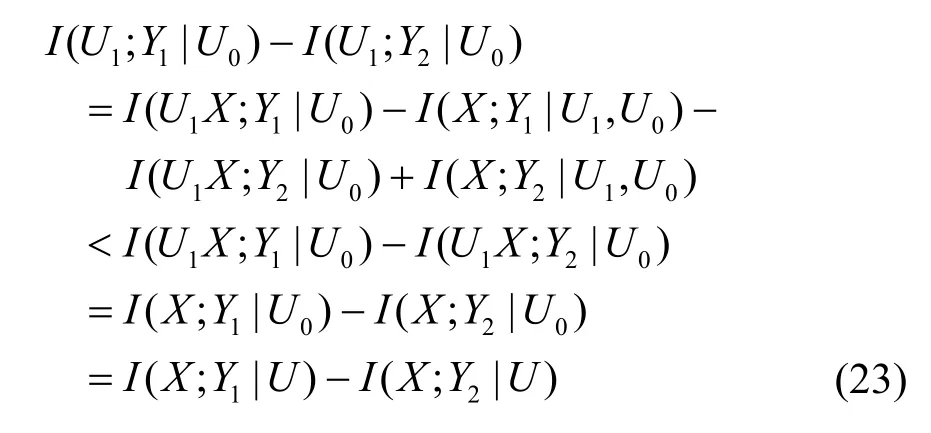
综合式(21)～式(23)，L4是L'3的一个外界，证毕。

在衡量广播信道 p(y1,y2|x)的 Y1和 Y2的能力差异时，more capable是比较弱的约束条件，对于较强的约束条件less noisy或退化关系时，L4也成立。

4 结束语

本文研究相关信源在广播信道下可靠安全传输的问题。基于分离信源信道码，得到了相关信源在一般广播信道下可靠和安全传输的可达允许信源区域的内界，并给出了达到信源信息部分绝对保密的条件。当满足退化信源集或I(X;Y1)＞I(X;Y2)时，分别得到了可靠和安全传输的最优限制条件，此时分离信源信道码为最优码，香农信源信道分离定理依然成立。未来下一步的任务可以结合如下工作：如采用联合信源信道编码[18]，这会突破传统的编码结构，虽然会带来在编码效率上的提升，但也会给安全传输带来挑战；Tandon在文献[3]中讨论了在Gray-Wyner系统中不同种类的公共信息对疑义度的影响；Villard在文献[4]中提出了带边信息的有损单信源在窃听信道中保密传输的问题。

附录A 定理1证明

对充分性证明。对所用的信源信道编译策略码做简要描述，分为如下几个步骤。

1) 信源编码器：使用 Gray-Wyner码将双信源序列映射成信源消息组 ( M ,M , M )。通过码率分别为012R0、R1、R2的三路无噪线路分别将M0、M1、M2发送到信道编码器。

2) 信道编码器：将 M0、M1、M2分别一一映射为信道消息W0、W1、W2。再基于Xu等人的保密编码策略[10]对消息进行信道编码，产生信道传输码字 xn。

上述编码策略可看作由2个环节组成：信源编译码与信道编译码。其中，信道编码策略与Xu相似，只是本文删除了如下限制条件[10]

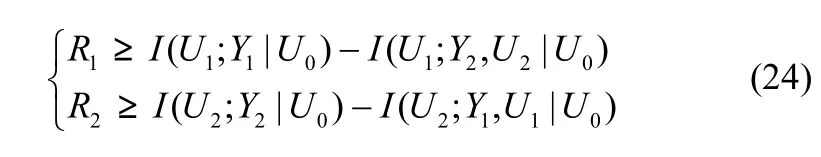
即本文不再要求消息速率R1和R2一定要大于信道的安全容量，这是因为在本文中信道消息速率还要受到信源编码的影响。在信道编码环节中，对变量的使用称谓基本延续Xu在文献[10]中的定义。

W∈ W = { 1,… ,2nR0}作为信道传输的公共消息，00W∈ W ={1,… ,2nR1}和W∈ W = { 1,… , 2nR2}作为信道的私密1122消息分别发送给译码器1和译码器2。进一步将W1划分为W∈ W ={1,… ,2nR10}和W∈ W = { 1,… ,2nR11}，W2划分为10101111W∈ W ={1,… , 2nR20}和W∈ W = { 1,… ,2nR22}， 其 中 ，20202222R1=R10＋R11，R2=R20＋R22，W10和 W20指能够同时被译码器1和译码器2进行消息译码。这种速率划分的目的是考虑到当 R0＜min{I( U0; Y1) ,I( U0; Y2)}，公共消息的传输不能充分地利用公共信道，故将W10和W20也作为公共消息借助于该信道进行传输。说明：这里的公共信道或私人信道是一种逻辑上的表达，实际上都是同一物理信道；与Xu不同的是，本文还将讨论W10和W20为空集时的情况。

1) 随机码生成

① 信源码字：固定某一输入分布 p ( v| s1, s2)。随机生成2nR0个码字 vn(m )， m ∈ { 1,… , 2nR0}，码字由独立同分布00的n个字母V构成，V服从分布 p ( v)；均匀地将含有序列集合等分割成 2nR1个小舱（记为bin），bin的下标为m1，m∈ { 1,… , 2nR1}；相似地均匀地将序列等分割成 2nR2个1bin，bin的下标为m2， m2∈ { 1,… , 2nR2}。

(R0,R1,R2)∈RG-W（见式(7)）且满足 Markov 链 S1－VS2，易知消息M0、M1、M2互相独立。

② 信道码字：固定某一信道输入分布 p ( u0) p( u1|u0)⋅p( u2|u0)p( x| u1, u2)。首先做如下定义：

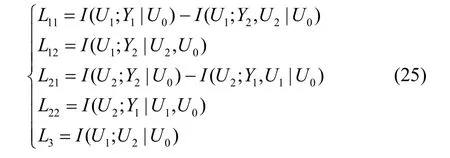
随机生成2n(R10+R20+R0)个码字码字由独立同分布的n个字母U0构成，U0服从分布 p ( u0)。然后针对每一个生成2n(L11+L12+L3)个码字i′∈ { 1,… , 2nL12}， i′ ∈ { 1,… , 2nL3}，码字由独立同分布的 n个字母U构成，U服从分布 p ( u |u )；相似地生成2n(L21+L22+L3)1110个 码 字(j, j′, j′)，j∈ { 1,… , 2nL21}， j′∈ { 1,… , 2nL22}，j′∈ { 1,… ,2nL3}，码字由独立同分布的n个字母U2生成，U2服从分布 p ( u2|u0)。对码字索引(i, i′, i′)和(j, j′, j′)可通过“binning”技术来解释。例如，可以随机地将放置到2nL11个bin中，每个bin由i进行标识，记作bin(i)；进一步把bin(i)划分成2nL12个 sub-bin，被随机划分到其中一个 sub-bin中，记为sub-bin(i')。i''则是sub-bin(i')中的随机序号。Liu把这一编码技术称为“double-binning”[9]，如表1所示。

2) 编码

0

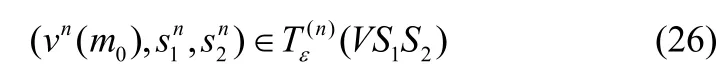
编码器0再将消息m0发送给信道编码器。编码器1根据要发送的信源序列，选择其所在bin，将bin的下标m1发送给信道编码器。同理编码器2将所在bin的下标m2发送给信道编码器。

② 信道编码：定义3个一一映射函数 g0,g1, g2，其逆映射为

信道编码器根据信源编码器发送过来的消息 m0、m1、m2，分别经过函数g0、g1、g2映射，得到信道消息w0、w1、w2，再经过消息划分得到w0、w11、w10、w22、w20。由此，可以首先得到(w ,w ,w )，然后从 2n(L11+L12+L3)个码字10200( i, i′, i′)中挑选一个码字用来传输w11。码字的确定分为3种情况，其中，后2种情况采用和Xu[10]一样的方式。

表1 double-binning

a) R11< L11。 2nL11个bin被均匀地划分为 2nR11个cell，每个w1对应一个cell。cell(w1)中有bin的数量为 2n(L11-R11)，随机挑选一个bin (i)。再从bin(i)的 2n(L12+L3)个码字中随机地挑选一个( i, i′, i′)。

b) L11≤R11≤L11＋L12。每个bin含有消息w1的个数为2n(R11-L11)，把 2nL12个sub-bin放入到 2n(R11-L11)个 cell中，从cell(w1)中随机挑选一个sub-bin，再从此sub-bin中随机挑选一个( i, i′, i′)。

c) L11＋L12

相同的步骤可根据w22来挑选码字(j, j′, j′)。此外还要求所挑选的码字( i, i′, i′)和(j, j′, j′)满足联合典型

3) 译码

随机码的译码方法采用联合典型序列译码方法，借助引理1和引理2。

进一步，根据 ( w10, w20, w0)，寻找一组消息(i, i′, i′)满足

根据(i, i′, i′)计算出w11。再由(w10,w11)得到消息w1。

② 信源译码：从信道译码中得到消息(w0,w1)，经过映射得到信源消息 (m , m ) 。从bin(m1)中挑选唯一满足01

4) 错误概率分析

除了信源编码和信源译码的错误概率计算，其他与Xu一致，略作说明。

根据式(26)，信源编码器会以错误概率接近于0的可能性找到一个消息m0，只要满足

根据式(27)，信道编码器会以错误概率接近于0的可能性找到一对消息(i',i'')，只要满足

根据式(28)，译码器1以错误概率接近于0的可能性找到唯一一组只要满足

根据信道码字的定义式(25)可以得到

进一步根据式(29)、式(34)，译码器 1以错误概率接近于0的可能性找到唯一一组(i, i′, i′)。由此

进一步可以有无差错译码(i, i′, i′)→w11→(w0,w1)→(m0,m1)。

12n(H(S1)-R1)。由 Gray-Wyner系统的可达域RG-W(见不等式组(7))可知

则有

由引理2、式(30)和式(36)可知，译码器1会以错误概率接近于0的可能性找到唯一。

5) 疑义度计算

对式(37)中步骤(a)～步骤(e)做如下解释。

步骤(a) 将疑义度拆分为两项，前项是信源编码带来的疑义度，后项是信道传输带来的疑义度。

步骤(b) 根据编码规则二元消息组(M1,M0)完全可以确定。

步骤(d) 由一一映射 W0= g0( M0)， W1= g2( M1)。

步骤(e) 公共信息W0可被任意接收者所译码，因此对疑义度不产生影响。

情况 1 当 H ( S1| V ) ＞ I( U1; Y1| U0) - I( U1;Y2, U2|U0)，即 R1＞L11。

步骤(38a)直接使用了Xu[10]的证明结果。由疑义度定义式(2)可得

情况 2 当 H ( S1| V ) ≤ I( U1; Y1| U0) - I( U1; Y2, U2|U0)，即R1≤L11。此时消息w1在广播信道中传输可以保证绝对安全。也就是说，译码器2通过无线信道无法知道关于w1的任何信息，但是这不等于绝对安全，因为译码器2可以通过对序列的译码得到公共消息M0，M0含有的信息。另一方面，由Markov链S1-V-S2可以推出M1和M0是独立的，由此M1是绝对安全，因此有

同理，在译码器2上的错误率分析和疑义度计算中，作者可以得到与译码器1对称的结果。

综合式(31)～式(36)和式(38)～式(42)，得到L1。

附录B 定理3证明

充分性证明：要求在定理1的不等式组中V=S2，去掉U2即得定理3。

必要性证明：首先考虑有一个(2nH(S2), 2nH(S1|S2),n ) 码可使得n长分组序列的译码错误率为。在上的概率分布为

根据费诺不等式(引理3)，再由 ( 2nH(S2), 2nH(S1|S2),n)码映射为消息的数目为 M0个数为 2nH(S2)，M1个数为 2nH(S1|S2)，则有如下不等式

1) 允许信源区域外界计算

步骤(47b)：应用费诺不等式性质(见式(44)～式(46))。

2) 疑义度外界计算

同时

综合式(47)、式(48)和式(49)，即得L3。定理3证毕。

[1] LIANG Y, POOR H V, SHAMAI S. Information theory security[J].Foundations and Trends in Communication and Information Theory,2009, 5(4-5)： 2009.355-580.

[2] CSISZAR I, KORNER J. Broadcast channels with confidential messages[J]. IEEE Transactions on Information Theory, 1978, 24(3)：339-348.

[3] TANDON R, SANKAR L, POOR H V. Multi-user privacy： the Gray-Wyner system and generalized common information[A]. Proc IEEE International Symposium on Information Theory[C]. Saint- Petersburg, Russia, 2011. 563-567.

[4] VILLARD J, PIANTANIDA P, SHAMAI S. Secure lossy source-channel wiretapping with side information at the receiving terminals[A]. IEEE International Symposium on Information Theory[C].Saint-Petersburg, Russia, 2011. 1141-1145.

[5] WYREMBELSKI R F, BOCHE H. Strong secrecy in compound broadcast channels with confidential messages[A]. IEEE International Symposium on Information Theory[C]. Cambridge, MA, USA, 2012.76-80.

[6] CZAP L, PRABHAKARAN V M, DIGGAVI S. Broadcasting private messages securely[A]. IEEE International Symposium on Information Theory[C]. Cambridge, MA, USA, 2012. 428-432.

[7] LY H D, LIU T, LIANG Y. Multiple-input multiple-output Gaussian broadcast channels with common and confidential messages[J]. IEEE Transactions on Information Theory, 2010, 56(11)：5477-5487.

[8] KHISTI A, LIU T. On private broadcasting over independent parallel channels[A]. IEEE International Symposium on Information Theory[C]. Cambridge, MA, USA, 2012. 433-437.

[9] LIU R, MARIC I, SPASOJEVIC P, et al. Discrete memoryless interference and broadcast channels with confidential messages： secrecy rate regions[J]. IEEE Transactions on Information Theory, 2008,54(6)：2493-2507.

[10] XU J, CAO Y, CHEN B. Capacity bounds for broadcast channels with confidential messages[J]. IEEE Transactions on Information Theory,2009, 55(10)：4529-4542.

[11] KRAMER G. Topic in multi-user information theory[J]. Foundations and Trends in Communication and Information Theory, 2008,4(4-5)：265-444.

[12] GRAY R, WYNER A. Source coding for a simple network[J]. Bell System Technical Journal, 1974, 53(9)：1681-1721.

[13] TIMO R, GRANT A, CHAN T, et al. Source coding for a simple network with receiver side information[A]. Proc IEEE International Symposium on Information Theory[C]. Toronto, Canada, 2008. 2307-2311.

[14] KAMATH S, ANANTHARAM V. A new dual to the Gács-Körner common information defined via the Gray-Wyner system[A]. Conference on Communication, Control, and Computing (Allerton)[C]. Monticello, USA, 2010.1340-1346.

[15] HAN T S, COSTA M H M. Broadcast channels with arbitrarily correlated sources[J]. IEEE Transactions on Information Theory, 1987,33(5)：641-650.

[16] TUNCEL E. Slepian-Wolf coding over broadcast channels[J]. IEEE Transactions on Information Theory, 2006, 52(4)：1469-1482.

[17] KANG W, KRAMER G. Broadcast channel with degraded source random variables and receiver side information[A]. Proc IEEE International Symposium on Information Theory[C]. Toronto, Canada,2008. 1711-1715.

[18] MINERO P, KIM Y H. Correlated sources over broadcast channels[A].IEEE International Symposium on Information Theory[C]. Seoul, Korea, 2009. 2780-2784.

[19] MURIN Y, DABORA R, GUNDUZ D. Joint source-channel coding for the multiple-access relay channel[A]. IEEE International Symposium on Information Theory[C]. 2012. 1937-1941.

[20] YANG Z, ZHAO S, MA X, et al. A new joint source-channel coding scheme based on nested lattice codes[J]. IEEE Communications Letters, 2012, 16(5)：730-733.

[21] GUNDUZ D, ERKIP E, GOLDSMITH A, et al. Reliable joint source-channel cooperative transmission over relay networks[J]. IEEE Transactions on Information Theory, 2013, 59(4)：2442-2458.

[22] LIU N, GUNDUZ D, GOLDSMITH A J. Interference channels with correlated receiver side information[J]. IEEE Transactions on Information Theory, 2010, 56(12)：5984-5999.

[23] GAMAL A E, KIM Y H. Network Information Theory[M]. Cambridge University Press, 2011.

[24] COVER T, THOMAS J. Elements of Information Theory[M]. New York： Wiley, 2006.

[25] GEL’FAND S I, PINSKER M S. Capacity of a broadcast channel with one deterministic component[J]. Problems of Information Transmission, 1980, 16(1)：17-25.