路灯电杆无模拉伸工艺研究
2013-10-27夏鸿雁
夏鸿雁,卞 清,吴 迪
(1.沈阳大学 机械工程学院,辽宁 沈阳 110044;2.东北大学 轧制技术及连轧自动化国家重点实验室,辽宁 沈阳 110004)
目前,城市建设、通讯、汽车、化工以及机械制造等工业领域对变断面管的需求越来越多,如热电偶不锈钢套管、特殊用途不锈钢空心连接轴、汽车用直拉管、路灯电杆等.路灯电杆一般都是采用圆管,近年来,为了提高其美观程度和更好地与环境配合,锥形方管开始被采用.国际上通用的锥形方管生产工艺是剪板、折弯和直缝焊接,成品尺寸精度差、成品率低、工艺复杂、设备庞大,难于实现自动化,产品成本高.采用无模成形取代现行工艺全部成形工序,将各种钢种方管直接拉伸成锥形方管,产品质量高、设备简单、生产率高,同时,在成形过程中完成形变热处理,提高产品的综合性能.同样,通过控制参数的变化,无模拉伸方法还可加工各种金属材料的任意变断面长尺异型管材[1-3].
本文设计了无模拉伸成形路灯电杆工艺.根据无模拉伸成形机理,给出了路灯电杆无模拉伸极限断面减缩率和主要工艺参数的确定方法,并提供根据产品尺寸确定拉伸道次及计算各道次拉伸半成品尺寸的方法.模拟实验研究表明,本文制定的工艺方案合理,工艺设备简单,解决了方断面锥形路灯电杆难于塑性成形的问题,具有一定的实用价值.
1 路灯电杆拉伸工艺设计
路灯电杆是断面为方形的锥形管,材料为低碳钢,σs=343MPa,路灯电杆零件图如图1.
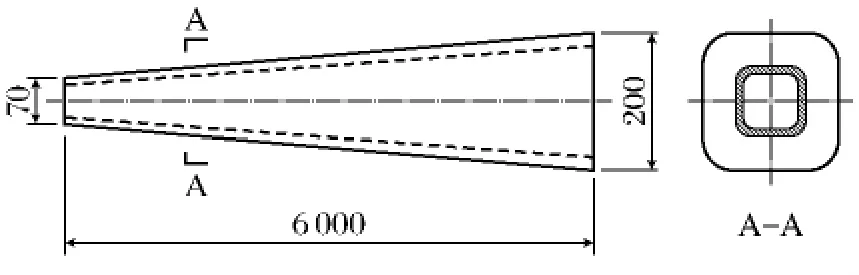
图1 路灯电杆示意图Fig.1 The diagram of wire-pole
现行工艺所生产的路灯电杆,因系钢板焊接,锥形方管壁厚相同,为增加路灯电杆使用稳定性,应加大路灯电杆下部的厚度.原料管的横断面外形尺寸为200mm×200mm,壁厚为12mm,根据体积不变原则,计算出原料管长度为2 945mm.
1.1 无模拉伸极限断面减缩率确定
无模拉伸时,变形端和变形完成端的变形力满足下列关系:

式中,A0、σ0分别为变形开始处温度为t0时的横断面面积与变形抗力;Al、σl分别为变形完成处温度为tl时的横断面面积与变形抗力.由式(1)有:
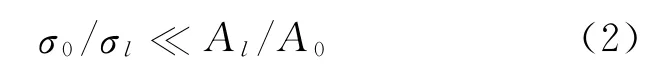
无模拉伸极限断面减缩率Rs的计算公式:
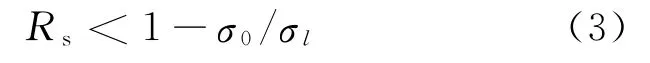
碳钢拉伸温度约为800℃,冷却后温度约400℃,取σ0=54MPa,σl=343MPa
根据式(3),极限断面减缩率:
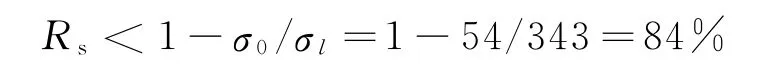
为保证顺利稳定拉伸,所用断面减缩率必须低于此值,取每道次断面减缩率为50%~60%.
1.2 拉伸次数确定
总断面减缩率:
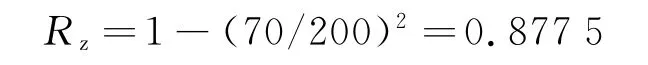
根据每道次拉伸断面减缩率极限值的限制,此总断面减缩率不能通过一道次拉伸实现,经计算,采用3道次拉伸工序.从外形尺寸为200mm×200mm,壁厚为15mm的方管拉伸成小端外形尺寸为70mm×70mm,壁厚为5mm的锥形方管,断面减缩率R和各尺寸间应满足下列关系:
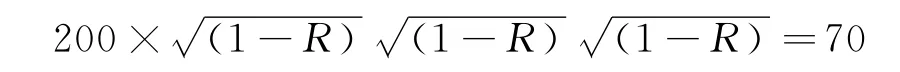
从上式解得:R=50.3%,采用3道次拉伸,每道次断面减缩率为50.3%,即可拉伸出要求的尺寸.
该方案第一道次将方管拉伸成前段是锥管后段是方管的管件,轴断面前段是锥形后段是平管;第二道次将第一道次拉出的平管拉伸成前段是锥管后段是方管的管件,轴断面前段是锥形后段是平管;第三道次是将第二道次拉出的平管全部拉伸成锥管,整个轴断面均呈锥形.三道次拉伸锥管角相同,各道次拉伸成品、半成品形状尺寸如图2所示.
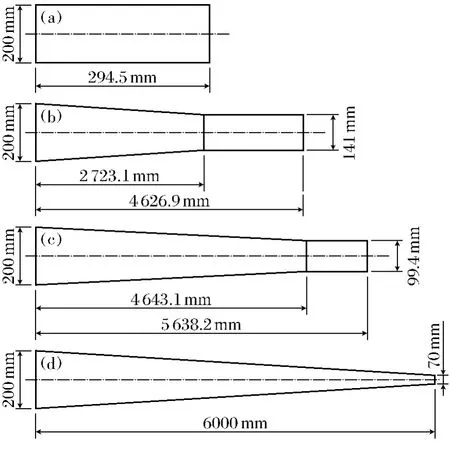
图2 路灯电杆各道次拉伸外形尺寸Fig.2 Shapes and dimensions of wire-pole after every drawing
各道次拉伸后方管横断面边长和长度计算如下:
第一次拉伸后,方管横断面边长:
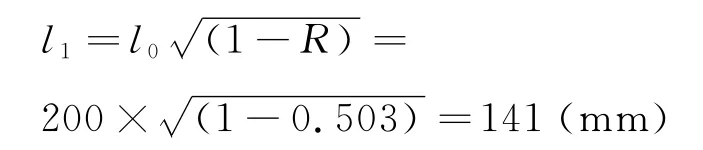
式中,l0为原料管边长.
根据体积不变原理,第一次拉伸后,前部分锥管的长度:
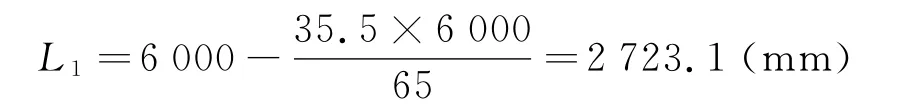
第一次拉伸后,后部分方管的长度:
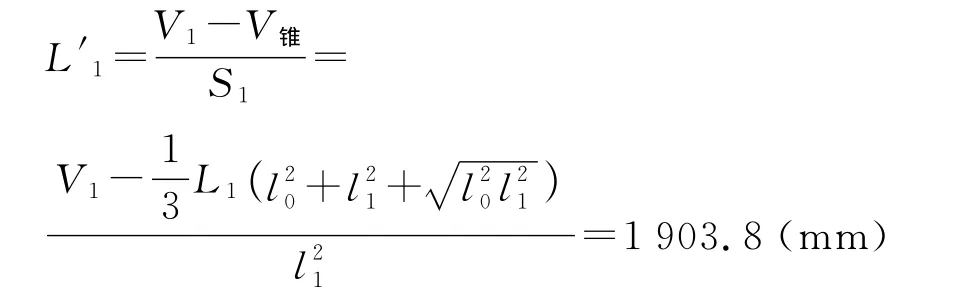
式中,V锥为第一次拉伸后锥管的体积;S1为第一次拉伸后锥管小端断面面积.
第二次拉伸后,方管横断面边长:

式中,V′锥为第二次拉伸后锥管的体积;S2为第二次拉伸后锥管小端断面面积.
第三次拉伸后,方管横断面边长:
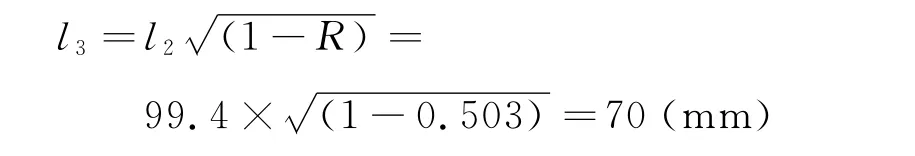
第三次拉伸锥管长度:
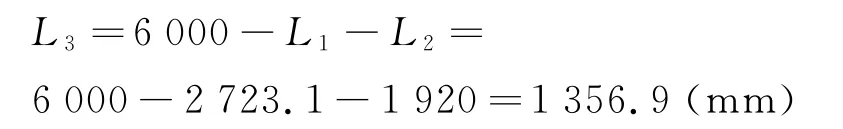
第三次拉伸后,后部分方管的长度:
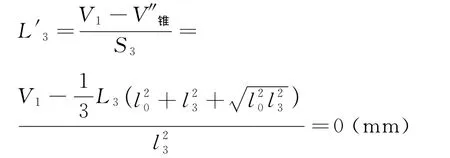
式中,V″锥为第三次拉伸后锥管的体积;S3为第三次拉伸后锥管小端断面面积.三道次拉伸锥管角相同.
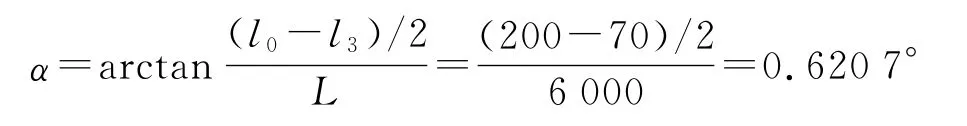
式中,L为锥管的总长度.
计算正确.
1.3 速度控制方法
路灯电杆无模拉伸模型如图3所示.由于受加热能力制约,冷热源移动速度受到限制.冷热源移动速度取决于拉伸材料对拉伸温度的要求,不宜作为速度变化对象,因此,通过改变拉伸速度的方式达到改变速度比的目的,使断面减缩率按要求变化,拉伸出给定的产品形状[4-5].在拉伸过程中,拉伸方向和冷热源移动方向反向,保持冷热源移动速度v2一定,控制拉伸速度v1按一定规律变化,拉伸出要求的产品.
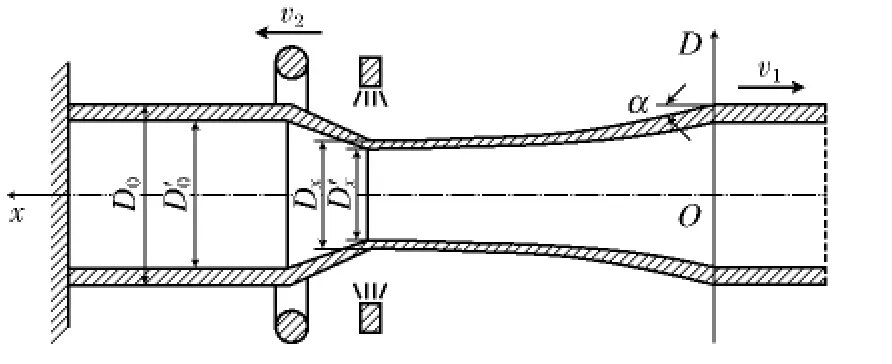
图3 路灯电杆无模拉伸模型Fig.3 Deformation model for tapered wire-pole dieless drawing
在拉伸过程中,第一、二道次是由方管拉伸成前段为锥管,后段为方管的管件,第三道次则是由方管拉伸成锥管.第二、三道次都是对工件进行局部加工,在上一道次拉伸出的锥管部分保持不变的基础上,只对上一道次拉伸出来的方管部分进行加工,从而降低了能源消耗.
2 模拟实验
2.1 实验设备
模拟实验在无模拉伸实验机上进行,尺寸模拟比为1∶10,实验机结构见图4.原料管为外形尺寸20mm×20mm,壁厚1.5mm的方管.材料为σs=343MPa的低碳钢,采用三道次拉伸.
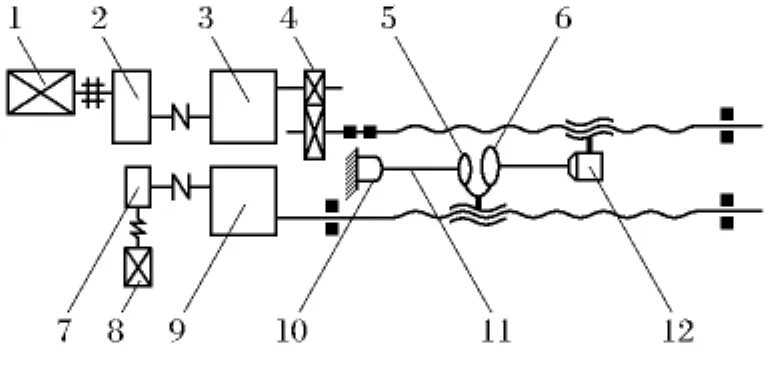
图4 无模拉伸实验机结构图Fig.4 The structure of dieless drawing experiment equipment
2.2 实验结果
根据锥形管拉伸速度控制数学模型[6],采用分段多项式逼近的方法,得出各道次拉伸速度与时间的变化规律,如图5所示.
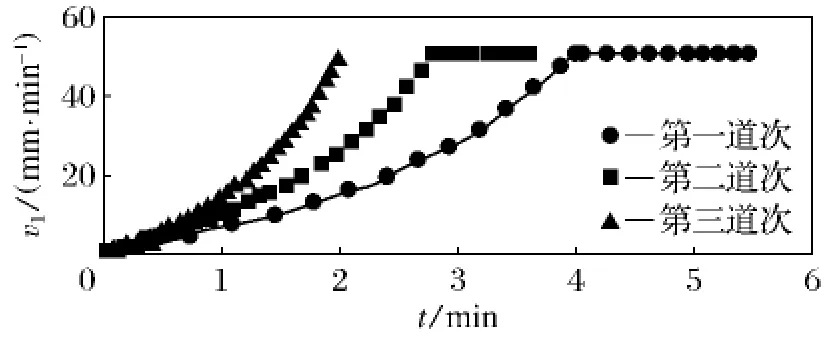
图5 各道工序拉伸速度v1的变化规律Fig.5 The variety law of every drawing speed v1
在模拟实验中,保持冷热源移动速度v2为50mm/min,采用了上述各个时间段上的主拉伸电机的理论速度值,通过对主电机速度进行控制拉伸锥形路灯电杆,得到较理想的加工结果.
在无模拉伸实验机上进行的模拟实验证明,无模拉伸路灯电杆壁厚不等,直径大的部分壁厚大,随直径减小壁厚减薄,底座部分的厚度大于上部.增加了使用的稳定性,同时,由于拉伸变形过程同时进行热处理,使电杆的强度和韧性都有所提高.模拟实验成品尺寸精度高,外观好,钢管尺寸精度及外观均较折弯焊接的钢管优越.
图6为加工件实测外形与计算外形比较,实测外形与计算外形吻合较好,三道工序的误差分别为6.7%、7.6%和6.1%.
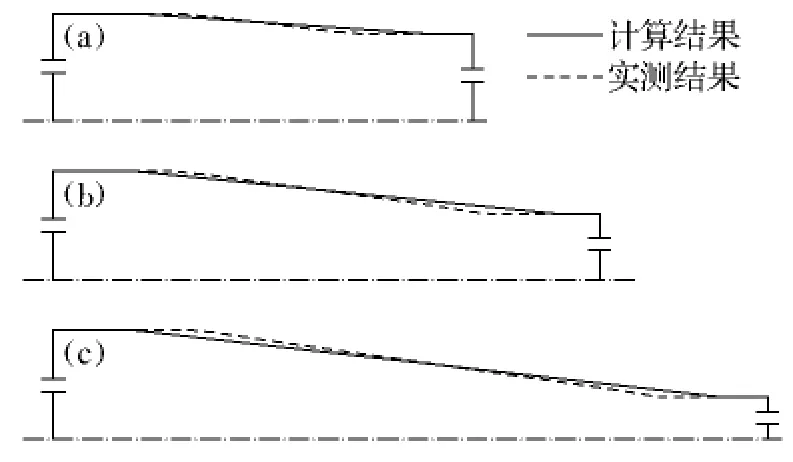
图6 拉伸件计算外形与实测外形的比较Fig.6 Comparison between calculated shape and measured shape of stretching piece
3 结 论
本文针对路灯电杆无膜拉伸工艺进行研究并取得了一定成果:
(1)制定了路灯电杆无模拉伸成形工艺方案,给出主要工艺参数的确定方法.
(2)采用分段多项式逼近的方式确定了路灯电杆各道次无模拉伸速度变化规律.
(3)根据无模拉伸稳定变形条件,确定了极限断面减缩率Rs的计算公式:Rs<1-σ0/σl.
(4)给出了根据极限断面减缩率确定拉伸道次的方法,提出了路灯电杆各道次拉伸成品尺寸的计算公式.
(5)无模拉伸的路灯电杆壁厚不等,底座部分的厚度大于上部,比折弯焊接钢管的稳定性高.
(6)采用无模拉伸方法所获得产品实测外形与计算外形吻合较好,尺寸精度及外观均较折弯焊接的钢管优越.
模拟实验得到的理想加工结果验证了路灯电杆无模拉伸工艺方案及主要工艺参数确定方法的合理性及可行性.该方法与传统工艺有明显的区别,设备简单,工艺合理,解决了路灯电杆难于塑性成形的问题.
[1] Wang Z T,Luan G F,Bai G R,et al.The Study on the Dieless Drawing of Variable Section Tube Part[J].Journalof Materials Processing Technology,1996,59(4):391-396.
[2] Luan Guifu,Cao Li,Dong Xuexin.Research on the Dieless Drawing of the Ti-6Al-4VAlloy[J].Acta Metallurgica Sinica,1999,35(1):616-620.
[3] Wang Z T,Luan G F,Bai G R.Study of the Deformation Velocity Field and Drawing Force During Dieless Drawing of Tube[J].Journal of Materials Processing Technology,1999,94(2/3):73-77.
[4] Wang Z T,Zhang S H,Luan G F,et al.Experimental Study on the Variation of Wall Thickness During Dieless Drawing of Stainless Steel Tube[J].Journal of Materials Processing Technology,2002,120(1/2/3):90-93.
[5] 夏鸿雁,吴迪.母线为抛物线形管无模拉伸速度控制的数学模型[J].沈阳大学学报:自然科学版,2012,24(3):22-26.(Xia Hongyan,Wu Di.Mathematical Model of Dieless Drawing Speed Control for Parabolic Pipe[J].Journal of Shenyang University:Natural Science,2012,24 (3):22-26.)
[6] 夏鸿雁,吴迪.确定锥形管无模拉伸速度制度的数学模型[J].东北大学学报:自然科学版,2009,30(6):833-836.(Xia Hongyan,Wu Di.Mathematical Model to Schedule Dieless Drawing Speed for Tapered Tubes[J].Journal of Northeastern University:Natural Science,2009,30(6):833-836.)
