部分压开压裂井早期裂缝线性流动方程推导
2013-10-27陈圣元中石油吉林油田分公司红岗采油厂采油五队吉林大安131300
陈圣元 (中石油吉林油田分公司红岗采油厂采油五队,吉林 大安 131300)
张 岩 (中石油川庆钻探工程公司地质勘探开发研究院,四川 成都 610000)
部分压开压裂井早期裂缝线性流动方程推导
陈圣元 (中石油吉林油田分公司红岗采油厂采油五队,吉林 大安 131300)
张 岩 (中石油川庆钻探工程公司地质勘探开发研究院,四川 成都 610000)
利用Newman乘积原理得到了各向异性部分压开垂直裂缝压裂井的压力响应表达式。通过Z函数的性质以及渐近式分析,获得了一个新的部分压开裂缝早期线性流动方程。上述研究结果不仅丰富了压裂井的不稳定渗流理论,而且对正确认识该类油井流体流动特征具有一定指导意义。
垂直裂缝压裂井;Newman乘积原理;早期裂缝线性流动方程
水力压裂技术已经成为改造油气藏实现油气增产的一项重要工艺措施,在石油开采中起到了很重要的作用。通常认为,当油气藏埋藏深度大于700m时,压裂将形成的是垂直裂缝。为了对压裂效果进行合理评价,就必须对井底压力和流入动态进行准确分析。目前对压裂井的不稳定试井分析,考虑裂缝高度与储层厚度相等的情况居多[1-3],而部分压开压裂情况的分析较少。为此,笔者对部分压开压裂井早期裂缝线性流动方程进行了推导研究。
1 利用Newman乘积原理得到的压力表达式
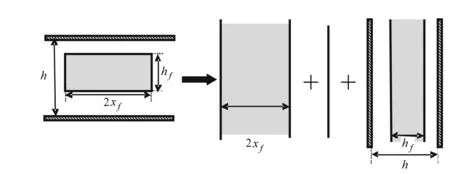
图1 利用Newman乘积原理分解的部分压裂井物理模型示意图
考虑均质油藏中的一口压裂井,为一上下边界封闭,水平方向无限大的油藏中的一条高度为hf垂直裂缝,裂缝中点距离油层底部的距离为zwm,裂缝以井筒为中心对称,裂缝半长为xf,裂缝流量沿长度方向均匀分布,不考虑裂缝宽度、流体的重力以及毛管压力的影响,气井以产量qsc(地面)生产。
根据文献[1],可以将部分打开无限导流垂直裂缝的三维渗流的瞬时点源函数分解为3个一维渗流问题的瞬时点源函数的乘积进行分析(见图1),即:

(1)
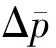
假定油藏水平方向各同向性,且油藏水平方向的渗透率为kh,则有kh=kx=ky。对于以点源强度dV进行生产时的瞬时点源函数有[4]:
(2)
(3)
(4)
式中,h为储层厚度,cm;ηx、ηy、ηz分别为X、Y、Z方向的导压系数,cm2/s;zw为源点所在的位置,cm;erf为误差函数。
定义无因次距离lD、无因次高度hD、无因次裂缝高度hfD、无因次压力pD、无因次时间tD等无因次变量:
将式(2)~式(4)式带入式(1)有:

(5)
其中:

(6)
式中,zwD为无因次条带源中点距离,cm。
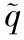
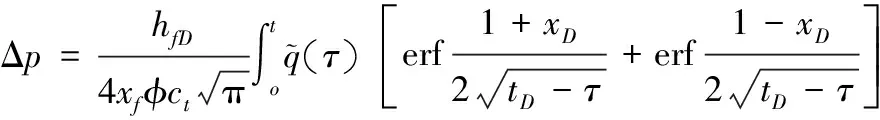
*Z(hfD,hD,zD,zwD,tD-τ)dτ
(7)


(8)
其中Z(hfD,hD,zD,zwD,τ)为Z函数,其表达式为[6]:
(9)
式(8)就是利用Newman乘积法得到的压力表达式。如果考虑井筒存储集系数(CD)及表皮系数(S),则井底标准压力pwD可表示为:
(10)
式中,pwD为无因次井底压力。
2 压力典型曲线
图2所示为考虑井筒储集系数CD和表皮系数S后的井底压力曲线。可以根据部分压开压裂井的压力典型曲线将渗流阶段划分为如下的4个流动阶段:①早期井储及其过渡流动阶段(流动阶段1),在压力导数曲线上表现为一个向上凸起的驼峰;②压裂井的早期线性流动阶段(流动阶段2),该阶段的压力导数曲线为斜率为0.5的直线;③部分压开井的球形流动阶段(流动阶段3),该阶段的压力导数曲线表现为斜率为-0.5的直线;当无因次裂缝高度越小时,该阶段的持续时间越长;④晚期的拟径向流动阶段(流动阶段4),该阶段的压力导数曲线为一条斜率为0.5的直线。
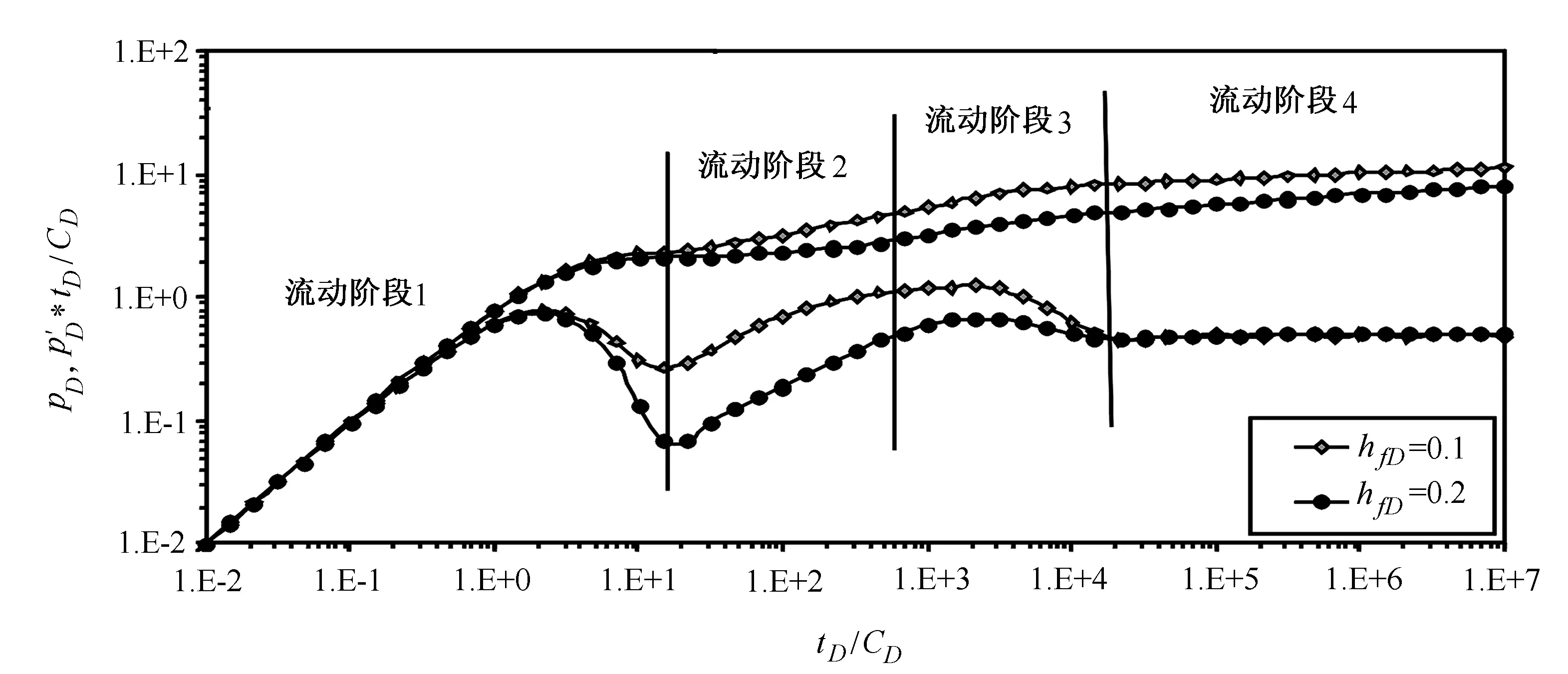
图2 考虑CD和S时部分压开垂直裂缝井的压力典型曲线
3 早期裂缝线性流动方程

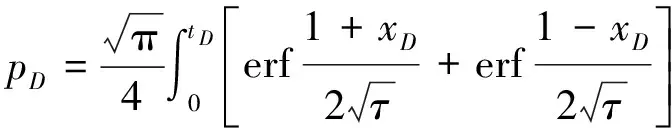
(11)
由于时间较短时:
(12)
则联立式(11)和式(12)进行积分可得:
(13)
在对井底压力进行计算时,由于xD=0.732,yD=0,所以裂缝内的线性流动方程为:
(14)
4 结 语
通过对均质各向异性油藏部分压裂井的不稳定渗流进行研究,利用Newman乘积原理,获得了部分压裂井的压力表达式。绘制了部分压开压裂井的压力典型曲线,通过对曲线进行分析,将部分压开压裂井的渗流阶段划分为早期井储及其过渡流动阶段、裂缝线性流动阶段、部分射开球形流动阶段以及晚期的拟稳定流动阶段。此外,利用渐进分析法和Z函数的相关性质,重新推导了早期裂缝线性流动方程。上述研究能够丰富压裂井的不稳定渗流理论,并对正确认识该类油井流体流动特征具有一定参考作用。
[1]Gringarten A C,Ramey H J.Unsteady state pressure distribution created by a well with a single infinite-conductivity vertical fracture [J]. Soc Pet Eng J Aug, 1974, 46(3):374-400.
[2]Cinco-Ley H, Samaniego V F. Transient pressure analysis for fracture wells [J].J Pet Tech Sept 1981, 54(6):1766-1789.
[3] Guppy K H,Cinco-Ley H,Ramey H J.Transient flow behavior flow behavior of vertical fracture well producing at constant pressure [J].SPE9963,1989.
[4]卢德唐,张联华,曾亿山,等.部分压开井渗流井底压力瞬时压力计算[J].中国科学技术大学学报,2001,31(4):443-447.
[5] Gringarten A C.Unsteady-State Pressure Distributions Created by a Well with a Single Horizontal Fracture, Partial Penetration, or Restricted Entry[D].PhD dissertation:University of Stanford,1971.
2013-01-23
陈圣元(1984-),男,助理工程师,现主要从事石油工程方面的研究工作。
TE353
A
1673-1409(2013)10-0133-03
[编辑] 李启栋
