位场各阶垂向导数ISVD算法及其在Matlab中的实现

2013-10-27西安石油大学地球科学与工程学院陕西西安710065

长江大学学报(自科版) 2013年10期

关键词：傅里叶二阶噪音

韩利 (西安石油大学地球科学与工程学院，陕西西安 710065)

段瑞锋 (陕西省地质矿产勘查开发局物化探队，陕西西安 710043)

白茹 (中冶陕压重工设备有限公司，陕西富平 711711)

位场各阶垂向导数ISVD算法及其在Matlab中的实现

韩利 (西安石油大学地球科学与工程学院，陕西西安 710065)

段瑞锋 (陕西省地质矿产勘查开发局物化探队，陕西西安 710043)

白茹 (中冶陕压重工设备有限公司，陕西富平 711711)

垂向导数在场分离及其确定场源体边界等方面有重要作用。介绍了计算位场各阶垂向导数的ISVD算法，并将其在Matlab中实现，给出了计算位场各阶垂向导数ISVD算法的部分Matlab源代码。研究表明，利用Matlab可以方便快速地实现ISVD算法并较为准确地获得位场各阶垂向导数。同时，与在频率域和空间域计算相比，ISVD算法计算的位场各阶垂向导数特别是高阶垂向导数，具有较好的稳定性。

位场；各阶垂向导数；ISVD算法；Matlab

在位场数据的处理解释中，垂向导数方法在场分离及确定场源体边界等方面具有重要作用[1-2]。综合二阶垂向导数(integrated second vertical derivative，ISVD)算法是M.Fedi等在2001年提出并应用于实际资料处理解释中的计算位场各阶垂向导数的新方法[3]，能够有效避免在频率域计算各阶垂向导数时傅里叶变换本身固有的吉布斯效应以及导数算子的高通滤波作用以及在空间域计算时以泰勒级数和拉普拉斯方程为基础的计算公式产生的截断误差。Matlab是一种科学的数值计算编程语言，具有简单易学、函数库功能强大和界面友好等特点，其主要功能包括数值分析、矩阵运算、信号处理和图形显示。利用上述功能编制Matlab程序，可以快速实现位场数据的计算处理[4-5]。下面，笔者对位场各阶垂向导数ISVD算法及其在Matlab中的实现进行了研究。

1 方法原理

1.1在频率域计算位场标量位

(1)

式中，u、v分别为X方向和Y方向的频率。

1.2在空间域计算位场垂向二阶导数

ISVD算法在空间域用位场的2个水平二阶导数依据拉普拉斯方程计算位场垂向二阶导数，因此计算垂向二阶导数的关键在于计算位场的2个水平二阶导数。以计算位场x方向水平二阶导数为例，设坐标原点在计算点上，并令：

(2)

应用最小二乘法对曲线进行拟合，当m=2时，用5个点的位场异常值计算的公式如下：

(3)

2 程序流程

频率域中的位场数据处理流程包括读入数据并扩边、二维傅里叶变换、在频率域计算、二维傅里叶反变换及计算位场垂向一阶导数和数据缩边并保存。以ISVD算法计算位场垂向一阶导数为例，详细说明其Matlab程序。

2.1读入数据并扩边

假设布格重力异常数据为BG.dat，即经过插值计算的等间距网格数据。为了减小二维傅里叶变换的边界效应，应对边界进行处理。利用Matlab以矩阵为单位进行数据处理的特点，将异常值读入到矩阵g(n,m)中，然后按照余弦公式：

(4)

将矩阵行列数扩边至2的整数幂，扩边后知阵temp1(n2,m2)满足边界值为零[6]。

2.2二维傅里叶变换

在Matlab中可以利用内建函数fft2快速地对异常值矩阵temp4(n2,m2)实现二维傅里叶变换，然后利用内建函数fftshift进行移频，即将零频移到矩阵中心位置，由此得到频谱矩阵为glfs(n2,m2)。该段程序如下：

glfs=fftshift(fft2(temp4))

2.3在频率域计算

在频率域进行位场转换，即异常值频谱矩阵glfs(n2,m2)乘以垂向积分算子qv，以获得转换场的频谱矩阵vfs(n2,m2)，其中ax、ay分别为x、y方向网格数据间隔，du、dv分别为x、y方向基频。该段程序如下：

du=1/(m2*ax);dv=1/(n2*ay);

vfs=zeros(n2,m2);

for i=1:1:n2

for j=1:1:m2

if i～=(n2/2+1)||j～=(m2/2+1)

qv=(2*pi*(((j-(m2/2+1))*du)^2+((i-(n2/2+1))*dv)^2)^0.5)^(-1);

vfs(i,j)=g1fs(i,j)*qv;

vfs((n2/2+1),(m2/2+1))=vfs((n2/2+1),(m2/2+1))-vfs(i,j);

end

2.4二维傅里叶反变换及计算位场垂向一阶导数

对转换场频谱矩阵vfs(n2,m2)进行移频、二维傅里叶反变换和取实，即可得到转换场矩阵vl(n2,m2)，其转换场即为布格重力异常的位，求其2个水平二阶导数矩阵vlxx(n2,m2)和矩阵vlyy(n2,m2)，然后依据拉普拉斯方程求其垂向二阶导数矩阵vlzz(n2,m2)，即为布格重力异常的垂向一阶导数。该段程序如下：

vl=real(ifft2(ifftshift(vfs)));vlxx=zeros(n2,m2);vlyy=zeros(n2,m2);vlzz=zeros(n2,m2);

for i=3∶1∶n2-3

for j=3∶1∶m2-2

vlxx(i,j)=2*(vl(i,j+2)+vl(i,j-2)-vl(i,j))/(7*ax^2)-(vl(i,j+1)+vl(i,j-1))/(7*ax^2);

vlyy(i,j)=2*(vl(i+2,j)+vl(i-2,j)-vl(i,j))/(7*ay^2)-(vl(i+1,j)+vl(i-1,j))/(7*ay^2);

vlzz(i,j)=-(vlxx(i,j)+vlyy(i,j));

end

2.5数据缩边并保存

这是数据扩边的逆过程，只取矩阵vlzz(n2,m2)中间与原始数据对应的部分，即可得到ISVD算法计算的布格重力异常垂向一阶导数矩阵vzz(n,m)。然后将矩阵转换为dat文件格式，并保存。该段程序如下：

vzz_temp=zeros(n,m);

vzz_temp=vlzz(cl1∶n2-cl2,rl1∶m2-rl2);

vzz_temp2=reshape(rot90(vzz_temp,-1),n*m,1);

vzz=cat(2,temp1(∶,1∶2),vzz_temp2);

save vzz.dat vzz -ascii;

程序代码中n、m、ax、ay分别为已知参数，以上代码在Matlab7.0中检验通过。

3 模型对比试验分析

单个棱柱体模型长20km，宽5km，顶部深度4km，底部深度10km，密度差为0.3×10-3kg/cm3，为了更加贴近实际地质情况，给原始重力异常值增加异常值1.25%的高斯噪音，即信噪比为80，采样间距0.2km。单个地质体模型如图1所示。

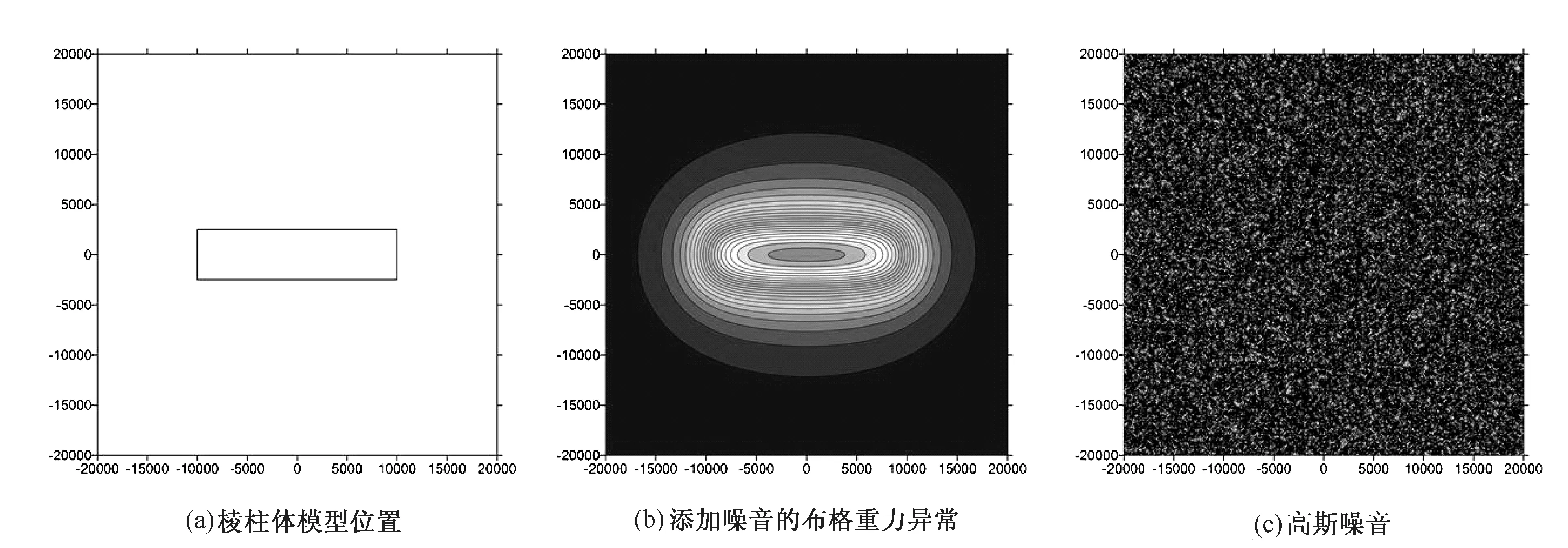
图1 单个地质体模型

分别应用ISVD算法以及在频率域和空间域计算模型重力异常的各阶垂向导数，计算结果如图2所示。从图2可以看出：①对于重力异常垂向一阶导数，3种方法计算的结果相差不大。②在频率域计算的垂向二阶导数由于垂向导数算子的高通滤波作用，将高频噪音放大。在空间域采用罗森巴赫Ⅱ式计算的重力异常垂向二阶导数与ISVD算法计算的结果相差较小，这是因为应用ISVD算法计算位场二阶垂向导数时，也是在空间域计算，只是两者采用的公式不同。③在频率域计算重力异常三阶导数时，高频噪音被严重放大，有效信号完全淹没在噪音当中。在空间域计算重力异常垂向三阶导数，由于截断误差的传递叠加，噪音较为严重，效果也不理想，而ISVD算法计算的重力异常垂向三阶导数，虽然也有噪音，但是其效果明显好于前2种方法。

ISVD算法之所以比在频率域和空间域计算位场各阶垂向导数稳定性要好，首先是因为位场在频率域内进行垂向积分，即乘以垂向积分算子，而垂向积分算子相当于圆滑滤波器，具有圆滑滤波作用，在一定程度上可以滤除部分高频成分，从而提高计算垂向导数的稳定性。另一方面是通过在空间域计算位场的2个水平二阶导数，依据拉普拉斯方程计算垂向二阶导数，有效地避免了在频率域计算水平二阶导数产生的震荡，同时也避免了直接依据哈克公式或其它空间域垂向导数公式计算垂向二阶导数产生的截断误差。