拟合优度检验功效比较

刘莲花 (海南医学院公共卫生学院，海南 海口 571199)

罗文强 (中国地质大学(武汉)数理学院，湖北 武汉 430074)

拟合优度检验功效比较

刘莲花 (海南医学院公共卫生学院，海南 海口 571199)

罗文强 (中国地质大学(武汉)数理学院，湖北 武汉 430074)

采用统计模拟的方法对6种正态性拟合优度检验方法的功效进行了模拟比较，模拟中分别采用Beta分布、Gamma分布、T分布和Lognormal分布4种不同的偏正态分布函数进行抽样，最终得出6种检验方法功效上的总体排序。

拟合优度检验；检验功效；统计模拟

拟合优度检验是统计理论的重要内容，其与实际应用有密切的联系。现实生活中常常需要根据给定的样本数据来检验样本是否来自某个特定的分布，以便进一步的获取样本的某些信息，如疲劳寿命、可靠度等。但是实际应用中常常出现这种问题：同一样本数据在相同的原假设分布下，有的拟合优度检验方法得出的结论是拒绝原假设，而有的拟合优度检验方法得到的结论是接受原假设。出现这种问题的原因是进行拟合优度检验时很容易犯“拒真”和“纳伪”2类错误。任何一种检验方法，犯2类错误都是不可避免的，然而对于同一样本，不同的拟合优度检验方法犯错误的概率却是不同的。一个好的检验，要求在控制第1类错误的前提下，第2类错误尽可能的小，也就是检验的功效尽可能的高，因此出现上述问题时，应以功效较高的检验方法得出的结论为主，且在进行拟合优度检验时，应尽量选择功效高的拟合优度检验方法。为此，笔者对不同的拟合优度检验方法的功效进行了模拟比较。

1 统计量

目前拟合优度检验的方法很多，因为正态分布是最重要的分布，也是实际应用最为广泛的分布，所以笔者主要针对正态性检验方法进行讨论。讨论的统计量有D、W2、A2、Zc、Za和Zk，其数值计算公式[1-3]如下：

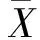
2 功效模拟方法

按照Neyman-Pearson原则[4]，在所有水平为α的拟合优度检验中，功效函数[4]在备择假设H1为真时越大，表明该检验越好,也即检验的功效越高，然而想求拟合优度检验的功效，其检验问题的备择假设，必须是具体的分布，所以笔者针对如下的具体问题进行讨论：

H0：F(x)=F1(x)H1：F(x)=F2(x)

拟合优度检验的功效一般不易直接求出，为此笔者采用统计模拟[5]的方法，模拟的具体步骤如下：

步2 计算用某种检验方法进行拟合优度检验时统计量的值，并记m次重复模拟中统计量的值落于拒绝域的次数为t；

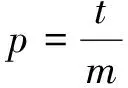
3 正态性检验功效比较

因为对于不同的偏正态分布以及不同的样本容量拟合优度检验的功效会有很大的差别，所以笔者主要选择Beta分布、Gamma分布、T分布、Lognormal分布作为备择分布进行抽样模拟[6-7]，所抽取的样本容量分别为10、30、50、60、70、80、100、150、200、250，模拟中的检验水平α=0.05，并在模拟中不断改变各分布的参数，以便得到在不同的偏度和峰度时的功效模拟值，表1～4分别列出了4种备择分布的参数取不同值时所对应的偏度及峰度值，图1～图4是分别从4种不同的备择分布中进行抽样模拟时的功效比较图形，最后通过分析图形对6种正态性检验方法的功效进行了总体的评价和排序。

3.1备择假设为Beta分布

从功效模拟图形1可得如下结论：①当备择分布Beta的偏度为零时，D统计量的功效是最高的，但是若偏度非零则D统计量的功效最低，这说明D统计量在检验时对峰度比较灵敏而对偏度不灵敏。②当备择分布偏度非零时，D统计量的功效随样本变化很小。③除D以外的其他5种统计量的功效随着备择分布偏度偏离于零的程度的增大而增加。④当偏度非零时，W2统计量的功效仅高于D统计量。⑤当偏度非零时，几种统计量的功效排序大致为：Za>Zc>Zk>A2>W2>D。

表1 Beta分布中参数取不同值时的偏度及峰度

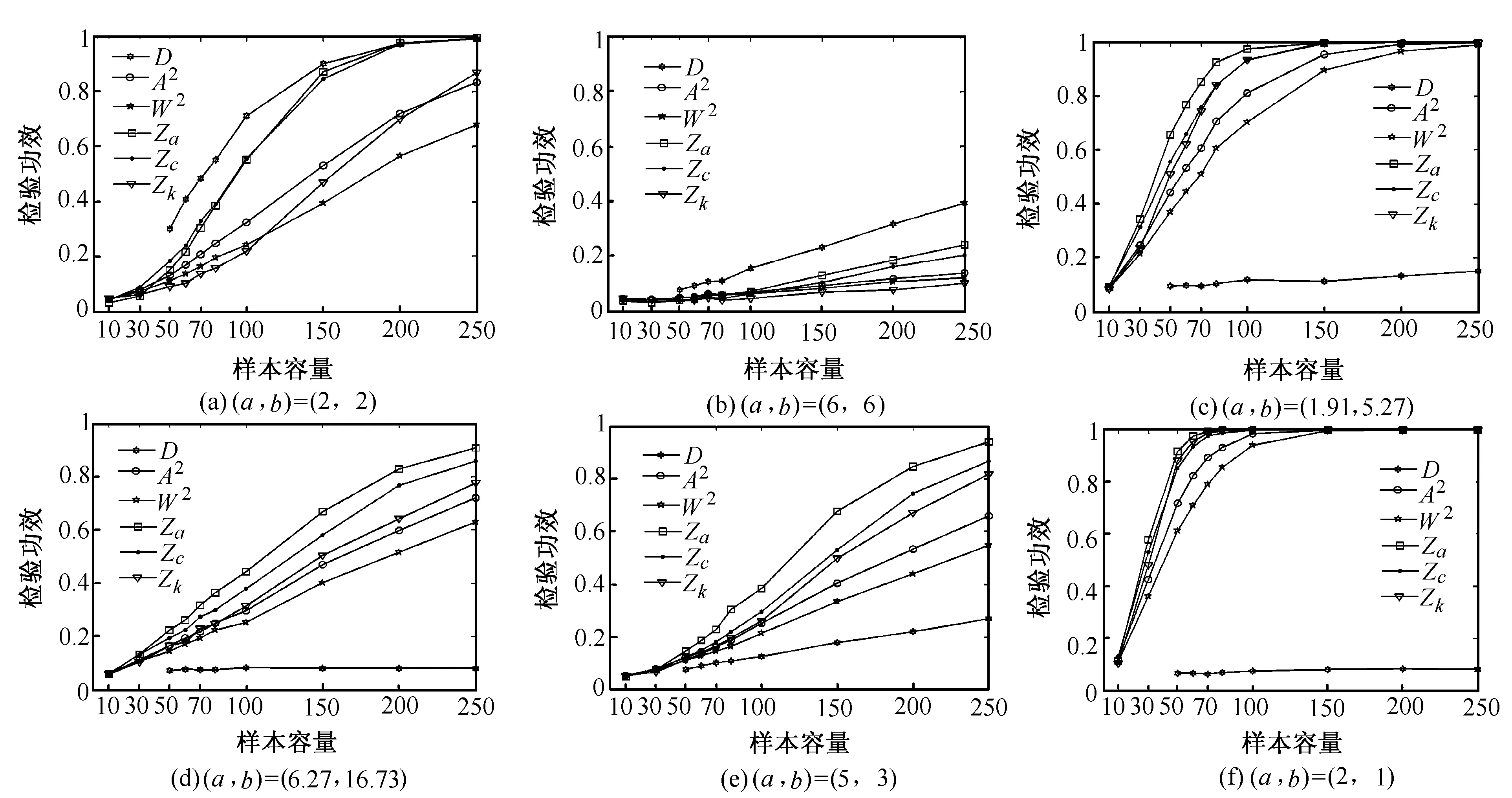
图1 Normal VS Beta(原假设是Normal分布，备择假设为Beta分布) 功效模拟比较图

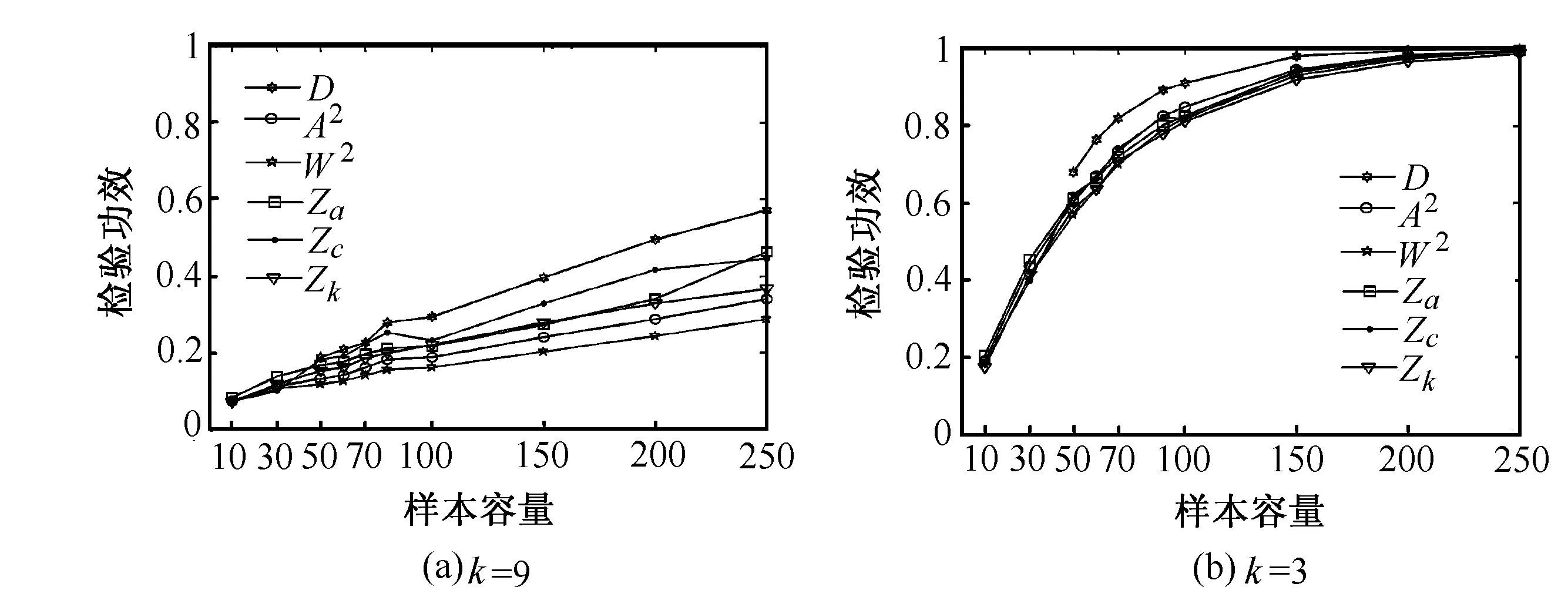
图2 Normal VS T功效模拟比较图

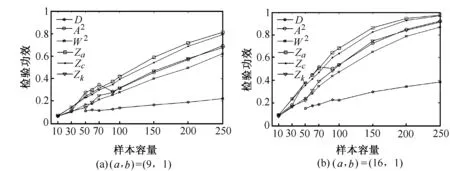
图3 Gamma 功效模拟比较图

3.2备择假设为T分布

从功效模拟图形2可得如下结论：①因为T分布是对称分布，即偏度为0，从图中可发现D统计量的检验功效是最高的，进一步说明了D统计量对峰度灵敏。②T分布中参数为3时偏离正态的程度大于参数为9时偏离正态的程度，相应的各统计量的功效也较高，这说明当备择分布偏离正态越严重，各检验统计量的功效越高。

3.3备择假设为Gamma分布

从功效模拟图形3可得如下结论：①2个图形中的备择分布的偏度都是非零的，所对应的D统计量的功效最低，进一步说明D统计量对偏度不灵敏。②当备择分布偏度非零时，W2统计量仅优于D统计量，而Za，Zc功效是最高的。

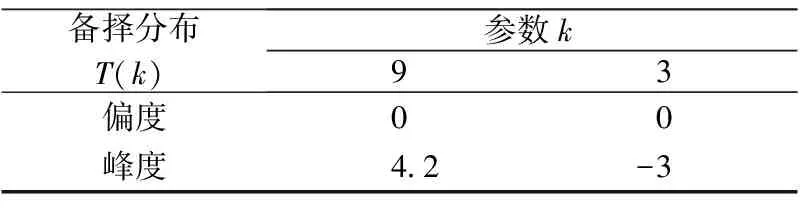
表2 T分布中参数取不同值时的偏度及峰度

表3 Gamma分布中参数取不同值时的偏度及峰度

3.4备择假设为Lognormal分布

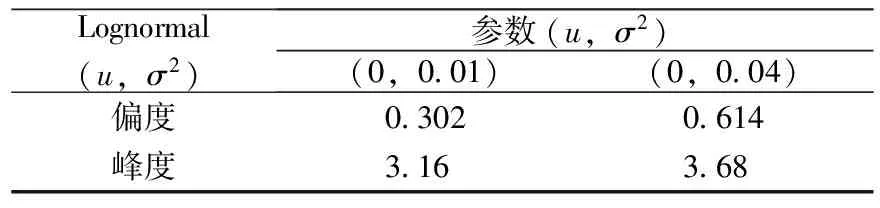
表4 Lognormal分布中参数取不同值时的偏度及峰度

图4(b)的备择分布偏离正态分布的程度较图4(a)备择分布严重，所对应的各统计量的功效也较高，进一步说明备择分布偏离正态分布越严重，各统计量的检验功效就越高。

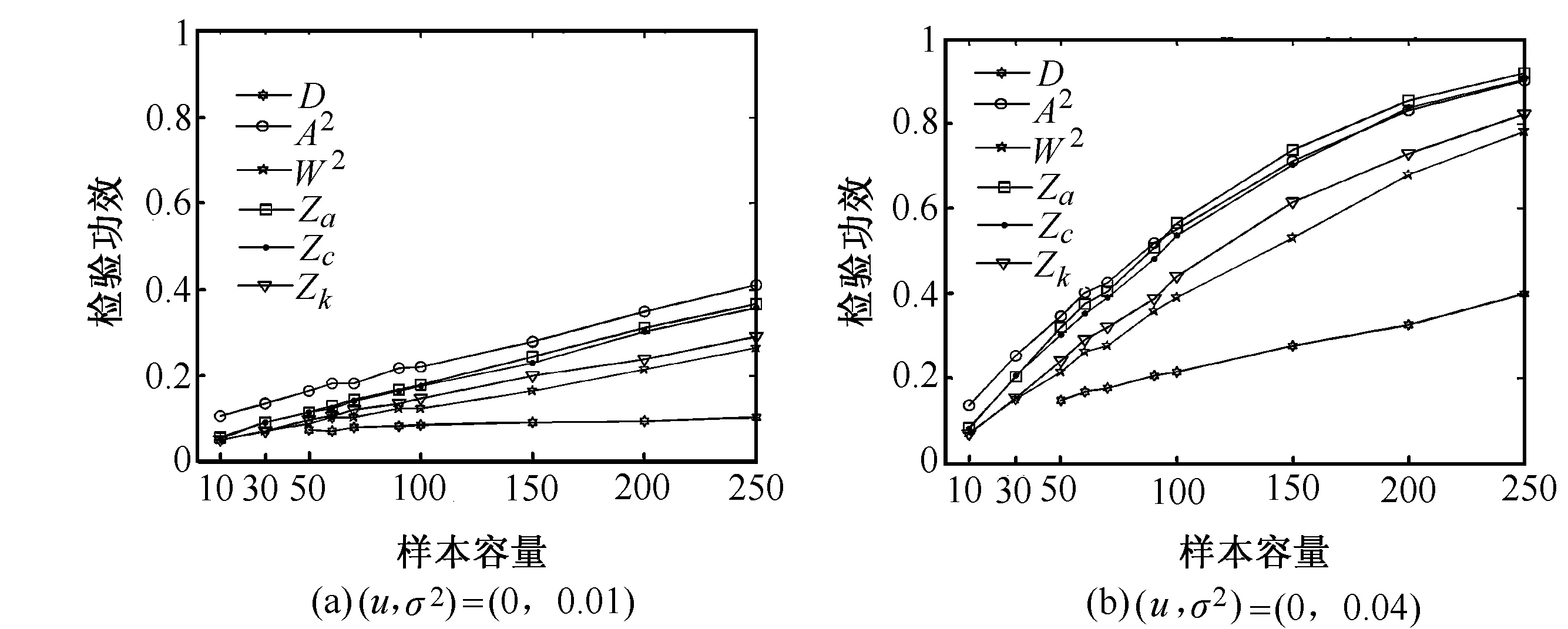
图4 Lognormal 功效模拟比较图

整体上观察上述4种备择假设下的功效模拟图形，可得到如下的总体结论：①D不是很好的检验正态性的方法，因为它只对峰度的偏差灵敏，而对偏度的偏差不灵敏。②当备择分布偏离正态的程度越严重，各检验统计量的功效就越高。③统计量Za、Zc、Zk对各种偏正态的分布都很有效且是稳健的。④在备择分布偏度非零的情况下，W2的功效仅高于D的功效。⑤从功效的角度看，6种统计量的总体排序为：Za>Zc>Zk>A2>W2>D。

4 结 语

采用统计模拟的方法比较了D、W2、A2、Zc、Za、Zk这6种统计量在检验正态性时的功效差异，通过对Beta分布、Gamma分布、T分布、Lognormal分布这4种分布进行抽样模拟，得出了6种统计量各自的优缺点，并对6种统计量在功效上进行了总体的排序。在进行拟合优度检验时，应该结合具体的原假设和备择假设，尽量选择合适的功效较高的检验方法，从而提高检验的可靠度。

[1]杨振海.拟合优度检验[M].合肥：安徽教育出版社，1994.

[2]Zhang J. Powerful goodness-of-fit tests based on the likelihood ratio[J]. J Roy Statist Soc，2002,64:281-294.

[3]Zhang J, Wu Y h. Likelihood-ration tests for normality[J]. Computational Statistics & Data Analysis, 2005,49: 709-721.

[4]茆诗松，王静龙，濮晓龙.高等数理统计[M].北京：高等教育出版社，1998.

[5]杨振海，程维虎.统计模拟[J].数理统计与管理，2006，25(1)：117-126.

[6]Surucu B.A power comparison and simulation study of goodness-of-fit tests[J].Computers and Mathematics with Applications, 2008, 56：1617-1625.

[7]Zhang Z Z. Some comments on the EDF Statistics of Goodness-of-Fit Tests[J]. Chinese Journal of Applied Probability and Statistics, 1996, 12(4):361-368.

2012-11-24

海南省自然科学基金项目(112006)。

刘莲花(1983-)，女，硕士，讲师，现主要从事拟合优度检验方面的教学与研究工作。

O212

A

1673-1409(2013)04-0014-03

[编辑] 洪云飞