FSK-DWDM四波混频的研究

张 鑫， 杜建新， 杨 辉

（南京邮电大学 光电工程学院，江苏 南京 210046）

0 引言

频移键控（FSK）凭借其高接收机灵敏度、对光纤的非线性有很高的容忍度、易解调、及其应用于光标记交换中在光载波频段加入或提取标签信息而不影响传输光强度等方面表现出来的优势，成为近年来光传输技术的研究热点[1-3]。目前已有理论研究表明在单信道10 Gb/s的传输系统中，FSK调制与差分相移键控(DPSK)调制具有相当的灵敏度，并且在实验条件下已经实现了在50 km的常规单模光纤（SMF）中得到速率为40 Gb/s，功率代价为0.8 dB的FSK信号[4]。随着密集波分复用(DWDM)技术的发展[5]，光纤的非线性效应特别是四波混频对其影响越来越大[6]。基于强度调制(OOK)调制格式，信道为非简并，入射波为矩形脉冲波并且考虑到DWDM系统中的比特序列的随机性、信道间脉冲走离效应等因素的影响情况下的四波混频效应已被研究[7]，运用类似的方法对调制格式为FSK，入射脉冲为啁啾高斯脉冲的情况进行讨论，考虑到多个信道对探测信道的影响，实例计算表明调制偏移频率与四波混频标准差的关系曲线图并不是简单的递增递减关系，而是当调制偏移频率取一定的值时，四波混频标准差有极小值，也就是最优值。特征宽度值的大小基本不会影响到这一曲线关系，但是较小的特征宽度值能得到较小的四波混频效应，然而群速度色散对这一曲线关系影响较大，其绝对值取很小的情况下，这一曲线基本呈线性递增关系，随着绝对值的增大，曲线呈震荡变化。

1 理论计算模型

FSK调制格式下光波电场表示如下：

式中，Pimax为脉冲峰值功率，f0为信道中心频率，Δf为调制偏移频率[8]，T0为比特宽度，V+，V_为脉冲群速度，τr为信道r内的随即序列相对参考信道的初始时延。

当比特信息为“1”时，比特序号为n的峰值功率归一化的啁啾高斯脉冲在入射点的光波的电场的复振幅可以表示为：

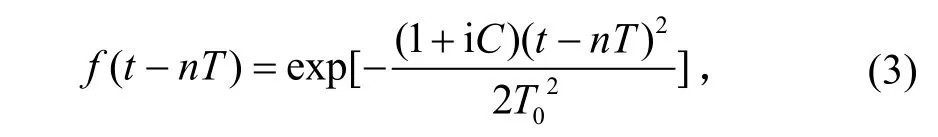
式中，C为初始啁啾参量。

考虑到群速度色散效应：

式中，β2表示群速度色散[9]。

假设未调制载波的中心角频率为ω0。当中心角频率由于调制变为ω0＋Δω时，对应的信号为比特“1”，反之，当中心角频率由于调制变为ω0－Δω时，对应的信号为比特“0”。

由于非简并四波混频效应产生的光场对比特“1”产生干扰对应的信道组合分以下3种情况：

在以下讨论中，公式中凡是出现A，B，C的分别对应上面3种情况。

3种情况下的四波混频噪声光电流：

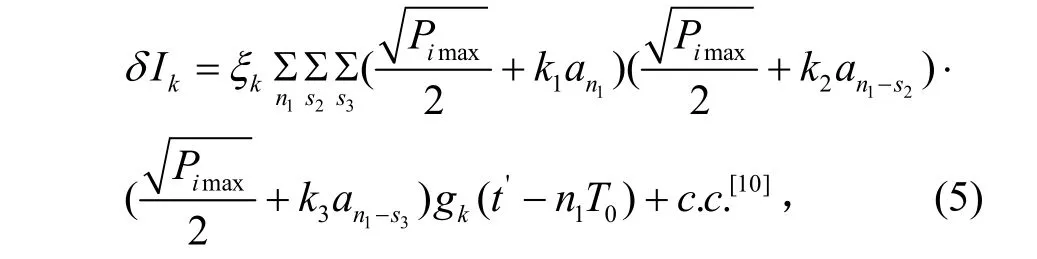
式中，k取 A，B，C，当 k=A时，k1=k2=k3=1，当k=B时，k1=1，k2=k3=-1，当 k=C时，k1=1，k2=k3=-1。

以ω1信道为探测信道：

式中，R为响应度，α为光纤的损耗系数，重叠函数g(t)的计算方法类似于参考文献[7]。

群速度的倒数表达式为：

式中，Δωi为各信道间的角频率间隔。

考虑到相关变量的随机性，可得：

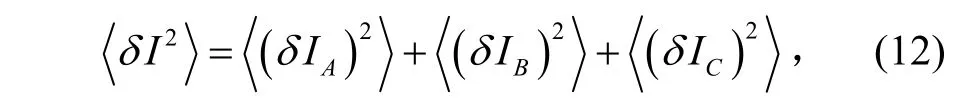
即四波混频效率满足：

噪声光电流δI( t)的均方值为一个时间变量，其表达式为：

2 仿真结果及讨论

设定 pimax=5 mw ,非线性系数γ=4.86 W-1km-1,以分贝作为单位的光纤损耗系数为0.217 dB/km，光波传输距离L=50 km ，单信道的速率为10 Gb/s，中心信道频率 fso=190.90 THz，3个信道的啁啾高斯脉冲的初始啁啾统一设为 0，系统相邻信道的信道间隔为100 GHz。考虑17个信道对中心信道的影响，以上参数在讨论中保持不变。

图1的参数设置为：群速度色散β2=-22ps/km，特征宽度T0=20 ps。从图1中可以发现四波混频标准差并不是递增递减的曲线，而是在30 GHz左右的地方有一个极小值。考虑到调制偏移频率越大解调越方便的因素可以认为调制偏移频率取 30 GHz左右时是比较合适的。

图2的参数设置为：群速度色散β2=-22ps/km,特征宽度T0取了3个不同的值分别为40 ps，60 ps，80 ps，这3个值分别对应的是三角形，星形，圆形标志的曲线。从图2中可以发现T0的不同并没有影响到图1中的最佳调制偏移频率值，但是特征宽度T0的大小是与四波混频标准差的大小呈正比的关系，为了减小四波混频的影响尽量的取较小一些的特征宽度值比较合适。

图3的参数设置：特征宽度T0=20 ps，群速度色散β2取了3个不同的值分别为-12ps/km，-5 ps2/km，-9 ps2/km，这3个值分别对应的是三角形，星形，圆形标志的曲线。从图3中发现群速度色散值对调制偏移频率与四波混频标准差的关系曲线有较大的影响，群速度色散取-12ps/km时，曲线基本呈现线性递增关系。而群速度色散取-52ps/km,-92ps/km时，曲线就呈现了起伏变化。

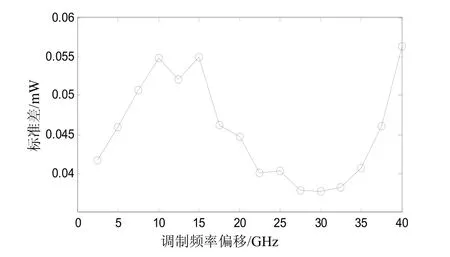
图1 β2=-2 ps2/km，T0=20 ps情况下四波混频标准差与调制偏移频率的关系

图2 T0取不同值，β2=-2 ps2/km情况下四波混频标准差与调制偏移频率的关系

图3 β2取不同值，T0=20 ps情况下四波混频标准差与调制偏移频率的关系

3 结语

考虑到DWDM系统中的比特序列的随机性、信道间脉冲走离效应等因素的影响。给出了调制格式为 FSK，信道为非简并，入射脉冲为啁啾高斯脉冲波情况下的四波混频噪声标准差的理论计算模型。在考虑到多个信道对于探测信道的影响的情况下用实例对其进行分析。研究结果表明在讨论调制偏移频率域四波混频噪声标准差的关系中发现它们并不是简单的递增递减关系，而是当调制偏移频率取一定的值时，四波混频标准差有极小值，此时的调制偏移频率为最优取值，特征宽度值不会影响到最优值的选取但是较小的T0值可以得到比较小的四波混频效应。然而群速度色散对调制偏移频率与四波混频标准差曲线关系影响较大，其绝对值取很小的情况下，这一曲线基本呈线性递增关系，随着绝对值的增大，曲线呈震荡变化。因此在具体的模型选取中需要综合考虑这些因素。

[1]何舟.高速光通信系统中先进调制格式研究[D].湖北:华中科技大学,2011.

[2]李明浩.先进调制格式的产生及其全光信号处理[D].湖北:华中科技大学,2006.

[3]杨桂林,电力线载波通信接口电路的设计[J].通信技术,2010,43(05):77-81.

[4]CHI Nan,YU Siyuan.Transmission Properties of a 40 Gb/s Signal in FSK Modulation Format[J].ECOC 2005 Proceedings,2005,114(03):729-730.

[5]刘佳,黄宏光.DWDM技术及其在城域网中的应用[J].通信技术,2009,42(02):18-20.

[6]沈建华,邵钟浩.四波混频对 DWDM系统的影响[J].光纤与电缆及其应用技术,2001(04):6-9.

[7]DU Jianxin.Analysis of Non-degenerate Four-wavemixing Crosstalk in DWDM System[J].Acta Physica Sinica,2009, 58(02): 1046-1052.

[8]INOUE K,NAKANISHI K,ODA K,et al.Crosstalk and Power Penalty Due to Fiber Four-Wave Mixing in Multichannel Transmissions[J]. Journal of Lightwave Technology,1994,12(08):1423-1439.

[9]DU Jianxin.Calculation of Degenerate Four-wavemixing Noise for Chirped Gaussian Pulse in DWDM System[J].Chinese Journal of Quantum Electronics,2009,26(06):1007-5461.

[10]KUMAR S.Analysis of Degenerate Four-Wave-Mixing Noise in Return-to-Zero Optical Transmission Systems Including Walk-off[J].Journal of Lightwave Technology,2005,23(01):310-320.