建筑物表面光伏组件最佳铺设方案的研究

杨若涵，文 艺，范镭耀，周羚君

（1.同济大学 电子与信息工程学院，上海 201804；2.同济大学 数学系，上海 200092）

1 引言

随着人类社会的飞速发展，能源问题俨然成为时下最热门的问题之一，科学家们对各种能源进行研究探索，太阳能以其安全、节能、环保、经济的优点脱颖而出，博得研究者的青睐。近几年，我国光伏产业经历了爆发式增长，已基本形成了涵盖多晶硅材料、铸锭、拉单晶、电池片、封装、平衡部件、系统集成、光伏应用产品和专用设备制造的较完整产业链［1］。虽然，有许多学者致力于研究太阳能，但是对于光伏电池实际应用于建筑物表面的研究并不多，而且并未给出具体铺设电池的算法。

太阳能建筑利用光伏电池发电，从而满足用户使用。为了使其能够得到推广，在现有材料的基础上，我们应当首先考虑使光伏电池产生利润最大化，以满足生产生活的需求。众所周知，光伏电池的工作效率并不高，因此如何使其利润达到最大化，如何进行电池的选择和铺设便成为了一个至关重要的问题。文中，对于评价光伏电池优劣给出了具体的算法，采用贪心算法配合最低轮廓线法得到最大利润的铺设算法，并对山西省大同市的单层建筑进行计算和分析。

2 不同方向阳光辐射强度与最佳倾角

2.1 阳光辐射强度

阳光辐射分为斜面阳光辐射和立面阳光辐射。因为在立面上的辐射可以直接进行测量，数据方便得到，因此不做过多的讨论。下面，我们重点讨论斜面的阳光辐射。

斜面上受到的太阳辐射包括直射辐射、散射辐射和地面反射辐射。因为一般地面反射辐射影响很小，可以忽略不计，则某一时刻斜面太阳辐射强度为

其中Ibβ为斜面直射辐射强度；Idβ为斜面散射辐射强度。

当阳光直射辐射在斜面上时，设斜面与水平面的夹角为β。太阳光入射角θ的计算公式［4］为

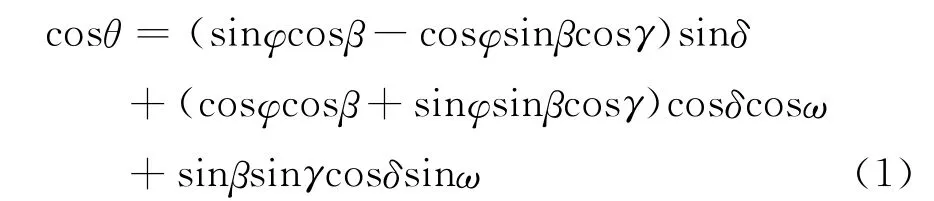
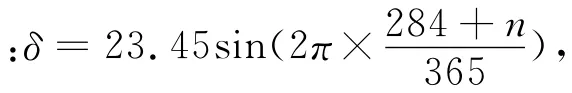
其中，Ibn为某时刻法向直射辐射强度。

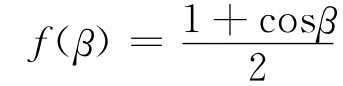
2.2 最佳倾角

在太阳能应用中，通常将采光面倾斜放置，为了使电池受到阳光辐射最大化，需要考虑架设电池板的最佳倾角。设倾角为β时一年中的总辐射量为H（β），由式（1）～（2）整理得

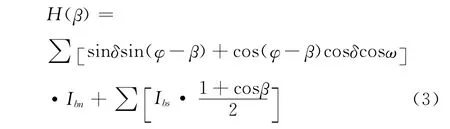
3 太阳能电池板的优劣性

现在市场上有许多不同型号的太阳能电池，如何选择电池成了一个至关重要的问题，因此我们需要对太阳能电池的性能进行评价。

每种电池板的成本M＝每峰瓦价格m×电池板额定功率p，即：M＝m·p

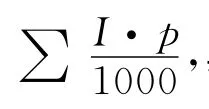
一般太阳能电池寿命期为35年，随着使用年数的增加，电池的转换率逐渐降低，前十年转换率为100%，第10～25年为90%，25～35年为80%。当前民用电价为0.5元／kwh。故35年内每块电池板的产值为

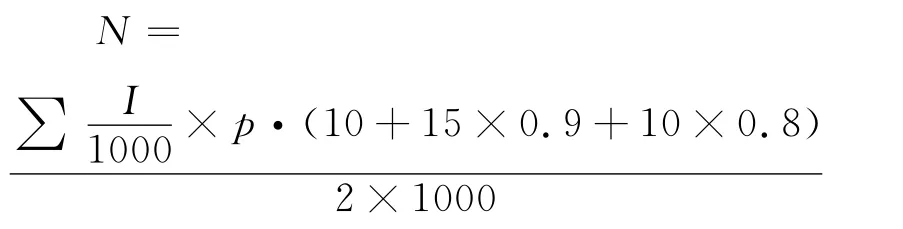
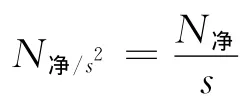
4 电池的选择与放置

根据上述方法可以对市场上所有太阳能电池进行评价，但由于所铺设墙面不同，我们不能简单地认为评价最优的电池最适合铺设，需要考虑墙面大小、逆变器选择等许多问题。

首先，采用初步规划，对铺设面进行初步判断。接着，运用采用贪心算法选择需要铺设的电池，并配合矩形排样中最低轮廓线法对电池的安放进行优化，从而得到利润最大的组合。最后根据逆变器情况进行分组，进行进一步优化。

4.1 初步规划

假设不考虑铺设方式，只考虑总体面积的情况下，以最大收益为目标，以铺设面积为约束，构建初步规划模型为

目标函数为：max＝∑N净·xi

其中xi为每种电池的数量。

约束条件为：∑si×xi＜S

4.2 贪心算法结合最低轮廓线的排列方法

首先根据太阳能电池的优劣性进行排序。根据贪心算法，选取最优性能的电池装入墙面，并循环此步骤。当最优性能电池无法再装入墙面时，选择次优性能电池装入墙面，以此类推，不断循环直至所有电池再无法装入墙面，循环结束。在放置太阳能电池时，采用最低轮廓线法［6］，每块电池进行放置的时候总是把电池放置在最合适的最低轮廓线上。这种方法可以保证电池铺设的最优性，以便达到最大铺设面积。

4.3 逆变器的选择

逆变器的选择，最终目的是获得最大利润。因此可建立单目标规划模型，以最大利润为目标，以额定电流I逆、允许输入电压范围U逆、额定功率P逆为约束条件。规划模型建立如下：

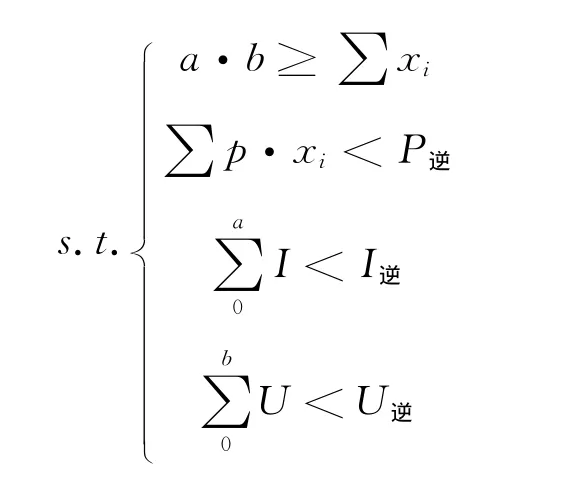
其中a为电池连接的串联数；b为电池连接的最大并联数。

5 发电量、利润以及回收年限的计算

5.1 总发电量、总产值、总利润的计算

设铺设光伏电池小屋各个墙体表面的总产值为Nx，各型号每块电池的产值为Ni，每种型号电池数量为xi，各个墙体表面电池的总成本为Mx，逆变器的价格为Inv，各面利润为Npx，发电量为W，电价为0.5元／kwh，逆变器效率为η＝0.94。故可以得到：各个墙体表面的总产值为Nx＝∑Ni＊xi＊η；各方向电池的总成本为Mx＝∑mi＊xi；各面利润为Npx＝Nx－Mx－Inv；设总产值为N，总利润为Np则有，总产值N＝∑Nx；总利润为Np＝∑Npx。

5.2 回收年限的计算

设由开始安装到第n年的总产值为V（n），该函数为分段函数，则有

而电池和逆变器的总成本为：电池成本＋逆变器成本＝∑（每块电池成本＊数量）＋逆变器成本，

当总产值大于等于总成本时，则可以收回成本，得到的n即为回收年限。

6 实例研究

我们研究在山西大同搭建的单层建筑，如图1所示。

考虑到实际原因，对于东西南北立面不架空铺设，只架空铺设南面屋顶。根据式（5）我们可以计算出最佳倾角为β＊＝34.51°。对于天窗预留问题，因为阳光辐射只要集中在正午时分，因此天窗预留口与天窗的投影位置相等。考虑到光伏电池并非直接贴于墙体表面，若铺设时电池略微遮挡预留窗口可以接受。则光伏电池架空安放示意图如图2所示。

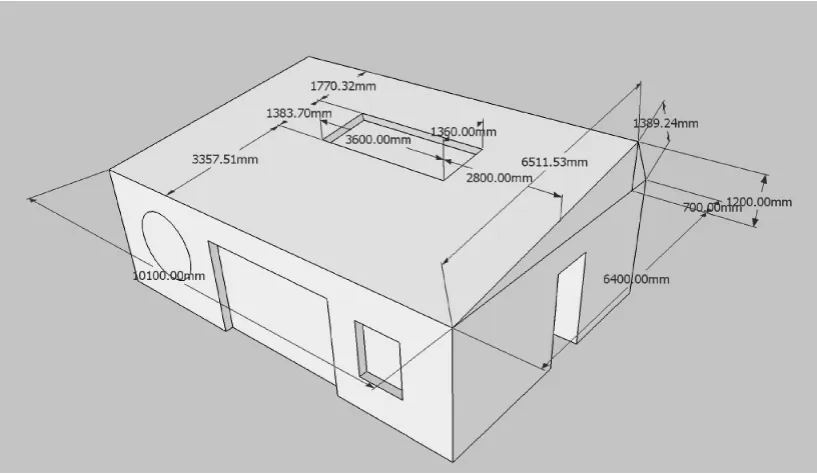
图1 太阳能房屋顶视图

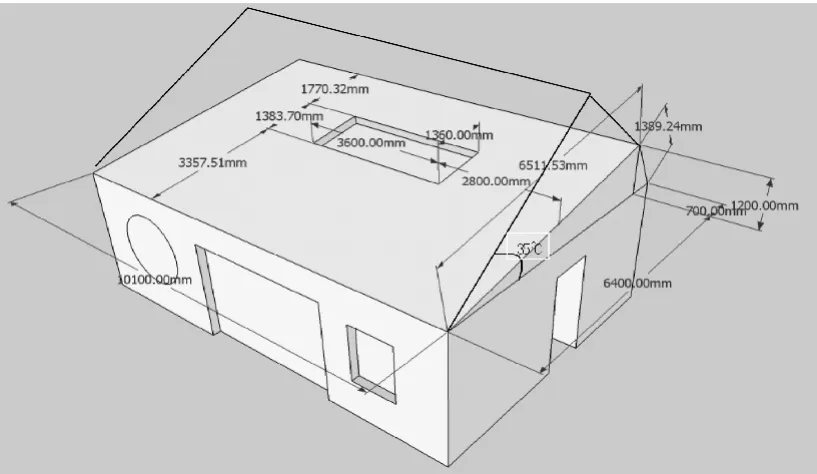
图2 太阳能房屋架空顶示意图

根据初步规划，可以知道当电池安放在北面屋顶、北立面和东立面时，在电池使用期限内无法回收，因此不考虑这三个面光伏电池的铺设。

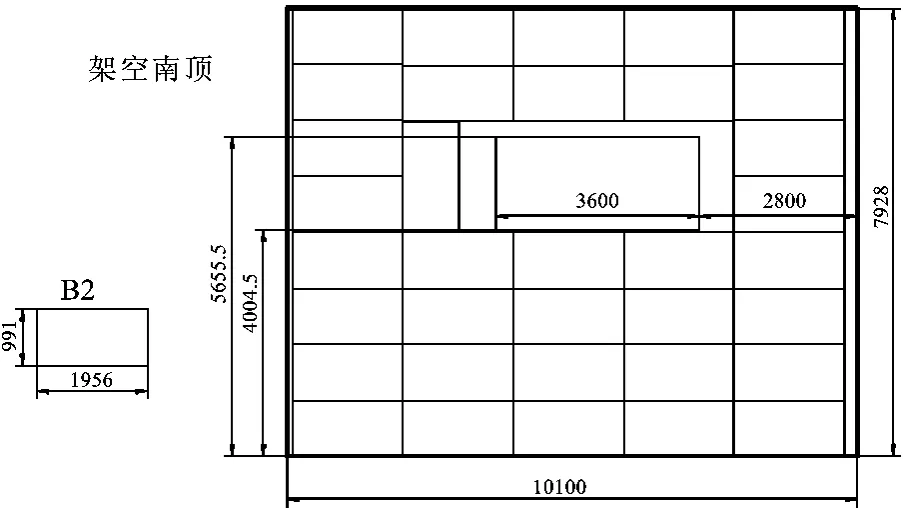
图3 南面屋顶电池架空排布

基于贪心算法结合最低轮廓线法，我们在南面屋顶将光伏电池排列，如图3所示。南面屋顶架空共用了35块B2电池，一个SN16逆变器和一个SN14逆变器。将这些电池分为两组，第一组由12块B2电池和一个SN14逆变器组成，其中每5块电池进行串联，得到2组电池进行并联，如图4所示；第二组由25块B2电池和一个SN16逆变器组成，其中每5块电池进行串联，得到5组电池进行并联，如图5所示。

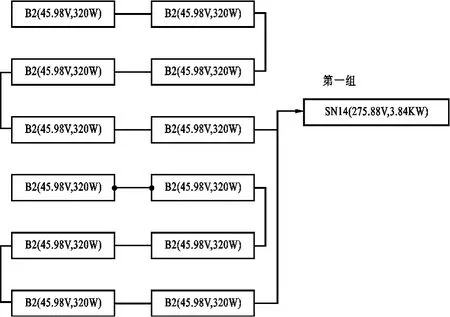
图4 南面屋顶第一组架空电池连接方式

南立面和西立面光伏电池排布的方法与南面屋顶相同，各项统计数据如表1所示：

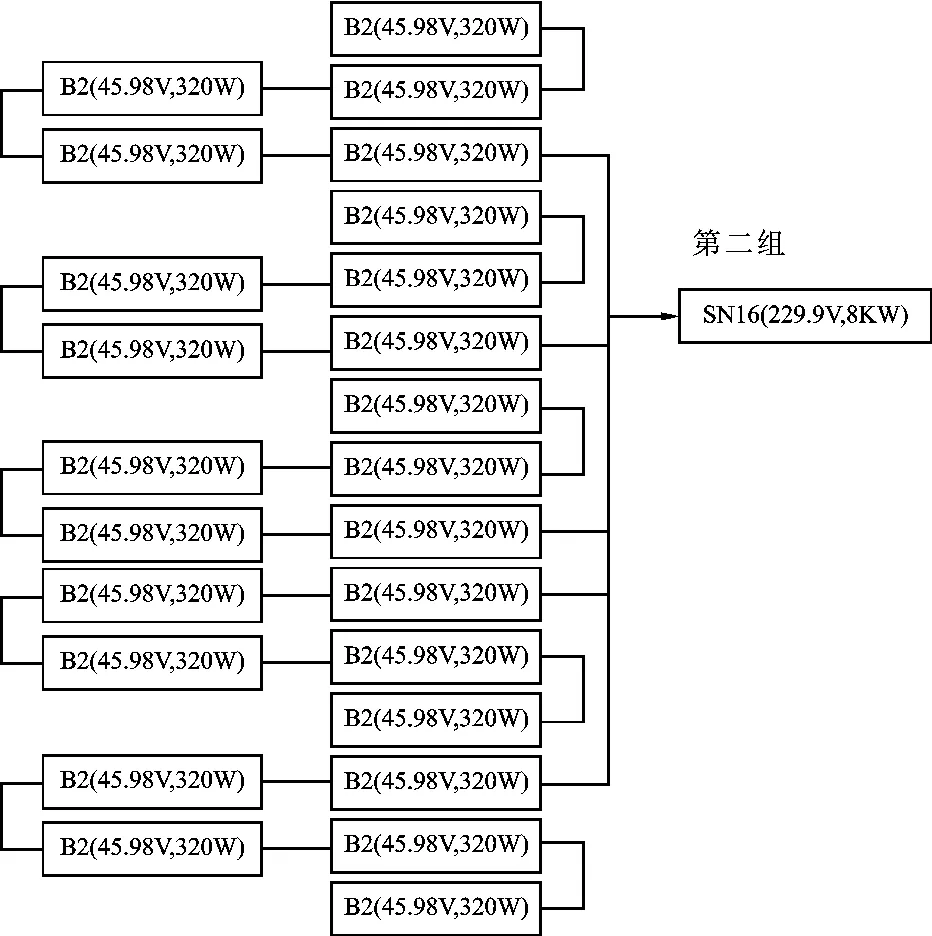
图5 南面屋顶第一组架空电池连接方式

表1 架空电池各项数据统计表

由表1可得35年的总产值为216231.3元，故每年的总产值Ny为

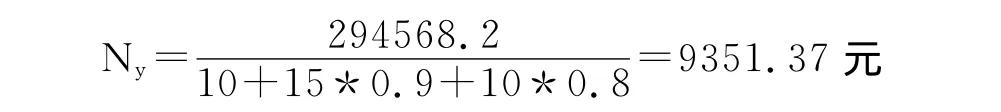
电池和逆变器的总成本为：电池成本＋逆变器成本＝150425.6＋66200＝216625.6元。当总产值达到总成本时，即可回收投资成本。根据式（6）可求得当n＝24时，V（n）＝21340.962＞216625.6元，所以需要24年才能收回成本。

通过统计数据［7］可以知道，2007年，我国平均农村人均用电量为452kwh，可以近似的得到35年农村人均用电量为15820kwh，折合电价7910元。假设平均每个房间住5个人，即每个房间35年用电费为39550元，小于总利润77942.6元。

据此，我们认为，太阳能发电可以先应用于农村地区。首先，相比于城市，农村地区用电量较少，光伏电池可以基本满足用户的供电需求；其次，在农村地区，房屋之间间隔较大，相互之间对太阳辐射量的影响较少，可以较大程度的发挥光伏电池的作用。

［1］王少南.太阳能建筑技术在国内外的发展［J］.新型建筑材料，2006，10：44－47.

［2］施韬，沈佳燕，蒋金洋.光伏建筑一体化研究及应用现状［J］.新型建筑材料，2011，38（11）：38－41.

［3］李群.“十一五”期间我国太阳能专业科技论文状况与分析［J］.可再生能源，2012，4：8－20.

［4］Hottel H C，Woertz B B.Performance of flat－plate solar－heat collectors［J］.Transactions of American Society of Mechanical Engineers，1991，64（91）：309－323.

［5］韩斐，潘玉良，苏忠贤.固定式太阳能光伏板最佳倾角设计方 法 研 究 ［J］.工 程 设 计 学 报，2009，16（5）：348－352.

［6］王贵宾，周来水，邓冬梅.基于模拟退火算法的矩形件排样［J］.中国制造业信息化，2006，15：65－70.

［7］江宝章，吴东升.农村人均用电量达城市的四成［N］.人民日报，2011－04－28（4）.