关于一个半离散非齐次核的Hilbert型不等式
2013-10-26黄臻晓杨必成
黄臻晓,杨必成
关于一个半离散非齐次核的Hilbert型不等式
*黄臻晓1,杨必成2
(1.湛江师范学院基础教育学院,广东,遂溪 524300; 2.广东第二师范学院数学系,广东,广州 510303)
应用权系数的方法及参量化思想,建立了一个具有最佳常数因子的、半离散非齐次核的Hilbert型不等式,还考虑了其等价式。
权系数;Hilbert型不等式;等价式
0 引言

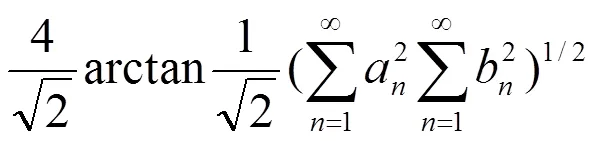
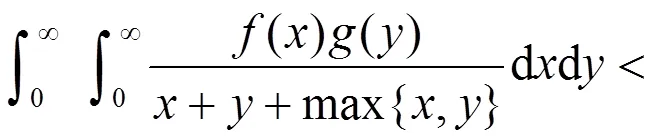
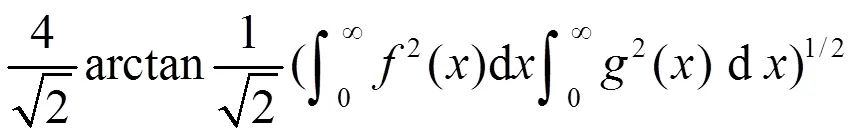




其主要结果是求出它的引入多参数的推广式及等价式。
1 引理
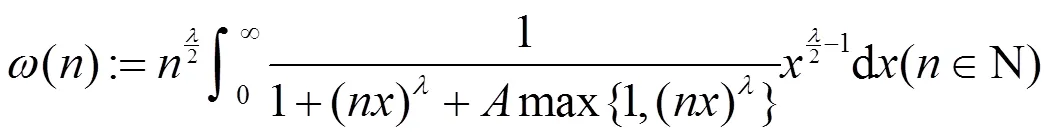
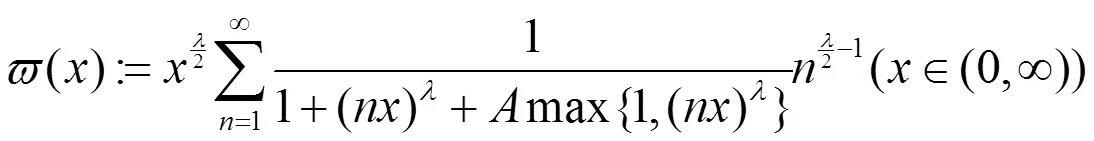
(N为正整数集)。则有如下不等式:

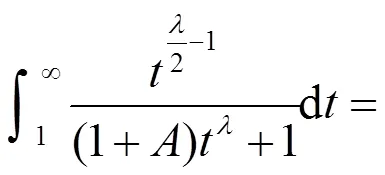

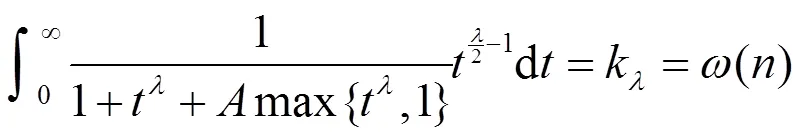
因而有式(7)。证毕。
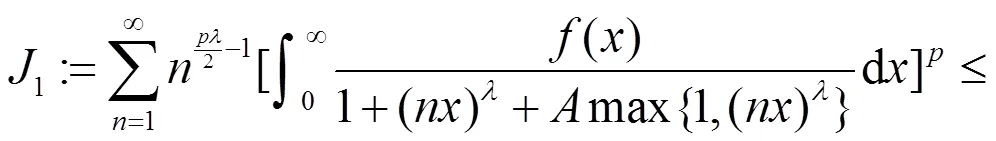

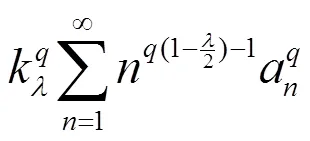

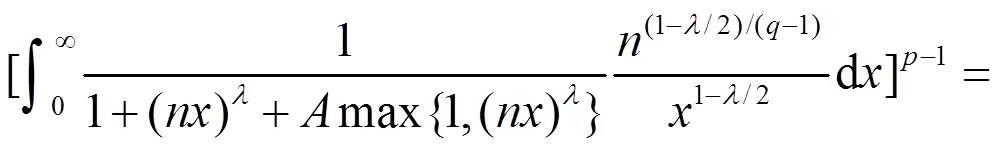
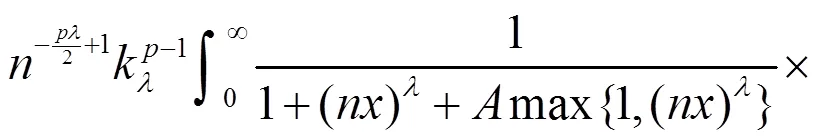
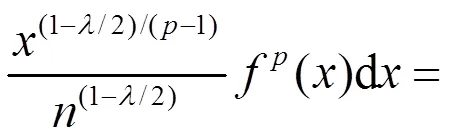
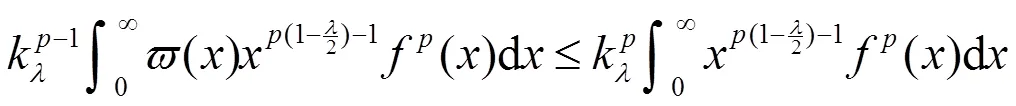
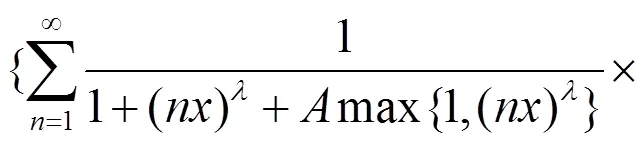

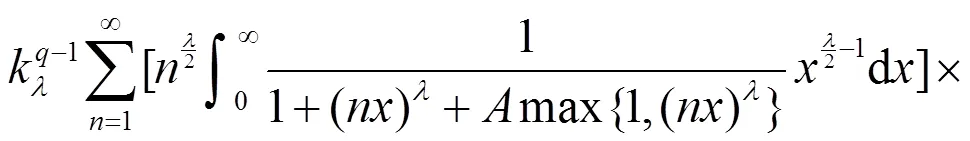
故式(9)成立。证毕。
2 主要结果


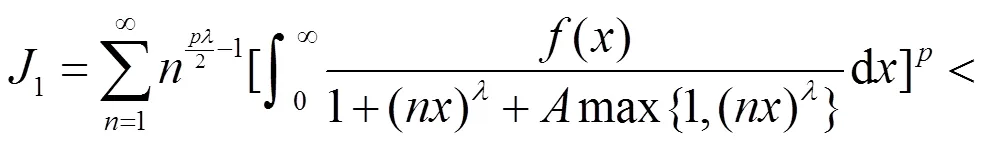
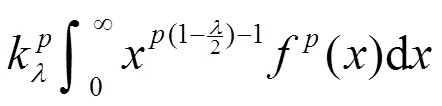
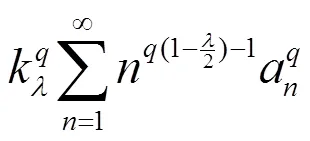
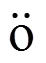


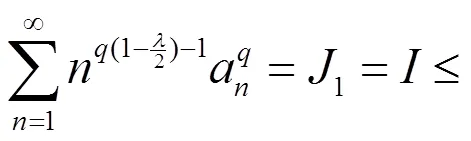

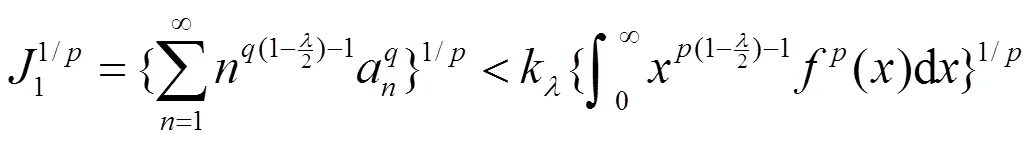
故式(13)成立,且它与式(12)等价。

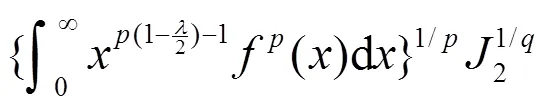
故由式(14),有式(12)。反之,设式(12)成立。取

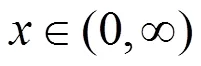
则由式(12),有
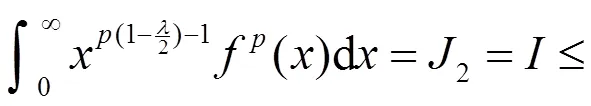

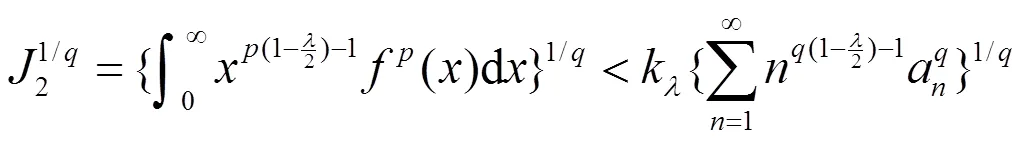
故式(14)成立,且它与式(12)等价。故式(12),式(13)与式(14)等价。


另一方面,由递减性及Fubini定理[10],又有

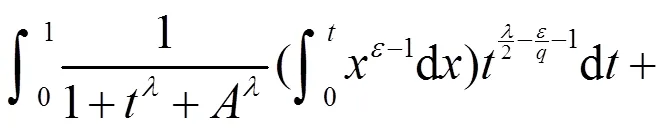
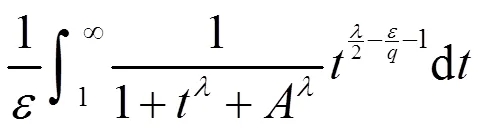
由式(19)及式(20),有
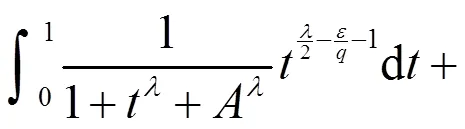
[1] Yang Bicheng. On a relation between Hilbert’s inequality and a Hilbert-type inequality[J].Applied Mathematics Letters,2008,21:483-488.
[2] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009.
[3] 黄臻晓.一个具有混合核的新的Hilbert型积分不等式[J]. 数学的实践与认识,2010,40(11):192-197.
[4] 黄臻晓.一个逆向Hilbert型积分不等式的最佳推广[J]. 山东大学学报:理学版,2010,45(2):107-110.
[5] 杨必成. 一个含参数且非齐次核的Hilbert型积分不等式[J].华南师范大学学报:自然科学版,2010(4): 31-33.
[6] 黄臻晓.具有两个参数的零齐次核的Hilbert型积分不等式[J]. 井冈山大学学报:自然科学版,2011, 32(5):5-8.
[7] 杨必成.一个半离散的Hilbert不等式[J].广东第二师范学院学报,2011,31(3):1-7.
[8] 杨必成.一个半离散非齐次核的Hilbert不等式[J].新乡学院学报,2011,28(5):385-387.
[9] 匡继昌.常用不等式[M].济南:山东科技出版社,2004.
[10] 匡继昌.实分析引论[M].长沙:湖南教育出版社,1996.
ON A HALF-DISCRETE HILBERT-TYPE INEQUALITY WITH THE NON-HOMOGENEOUS KERNEL
*HUANG Zhen-xiao1, YANG Bi-cheng2
(1.Basic Education College of Zhanjiang Normal University , Suixi , Guangdong 524300, China;2.Department of Mathematics,Guangdong University of Education, Guangzhou, Guangdong 510303, China)
By using the method of weight coefficient and the idea of introducing parameters, a half-discrete Hilbert-type inequality with the non-homogeneous kernel and a best constant factor is given. The equivalent form is considered.
weight coefficient; Hilbert-type inequality; equivalent form
O178
A
10.3969/j.issn.1674-8085.2013.03.001
1674-8085(2013)03-0001-04
2012-10-05;
2013-01-08
广东省高校自然科学基金重点研究项目(05Z026)
*黄臻晓(1968-),女,广东湛江人,副教授,主要从事解析不等式的研究(E-mail: sjxhzx@126.com);
杨必成(1947-),男,广东汕尾人,教授,主要从事算子理论与不等式研究(E-mail: bcyang@gdei.edu.cn).
