非线性横摇阻尼对运动和波浪扭矩的统一修正

李辉，张艺瀚，任慧龙

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

船舶在波浪中的运动以及波浪载荷预报的方法有切片法、二维半法和三维线性法等.基于三维势流理论［1］的线性计算法假设入射波是微幅波，船舶在微幅波中的运动也是微幅的.实际上，船舶在恶劣海况下的大幅摇荡运动非常明显，已不再满足线性化假设，属于非线性问题，其中横摇运动的非线性效应相比于其他摇荡运动更加突出.为了准确预报船舶的横摇运动和波浪载荷，必须考虑横摇阻尼的非线性效应.尤其对舰艇和工程类船舶，良好的横摇运动性能是其完成作战、作业任务的保证，准确的波浪载荷预报更是其结构强度可靠性评估的基础.因此，本文对于非线性横摇的研究具有深远的意义和较强的工程实用性.

横摇非线性可分为阻尼力矩、恢复力矩、附加惯性矩和波浪扰动力矩的非线性［2］，其中恢复力矩的非线性主要影响横摇频率，阻尼力矩的非线性主要影响横摇幅值，是国内外研究的重点.Nayfeh等［3］对于规则横浪中的船舶根据牛顿第二定律建立非线性运动方程.文献［4-5］研究了非线性恢复力矩及其线性化解法，使非线性恢复力矩的处理较为成熟.Eissam等［6］讨论了非线性横摇运动的解析解和数值解.但是，在基于势流理论建立的线性横摇运动方程中，精确计入非线性横摇阻尼十分复杂，目前除了横摇衰减试验方法［7］外，通常采用基于能量法［8］的等效线性化方法，得到近似经验公式，如贝尔登法［9］、米勒法、驳船经验公式法、临界阻尼系数法［10］等，针对不同船型，各种修正方法的效果不尽相同.

本文在考虑非线性恢复力矩的基础上，采用等效线性化方法确定非线性横摇阻尼系数，并计入横摇运动方程来修正船舶的横摇运动.另一方面，在求解运动方程后的波浪载荷计算中，如波浪扭矩，往往因为不能很好地将非线性横摇阻尼考虑进去而影响计算结果.本文在波浪扭矩的计算中，提出了一种按湿表面积插值分配的方法，有效地在波浪扭矩的计算中考虑了非线性横摇阻尼的影响.

1 非线性横摇阻尼

1.1 等效线性化原理

非线性横摇阻尼力矩与横摇运动的高次方有关，通常取平方阻尼规律函数表达式［11］:

相应的横摇运动方程为

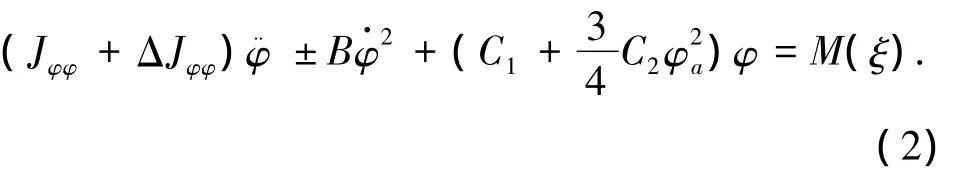
首先令φ=φmsin(nφt).平方阻尼力矩在一个周期内所作的功为

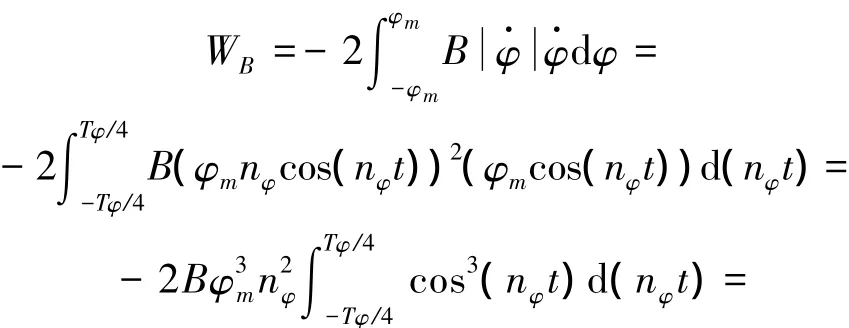
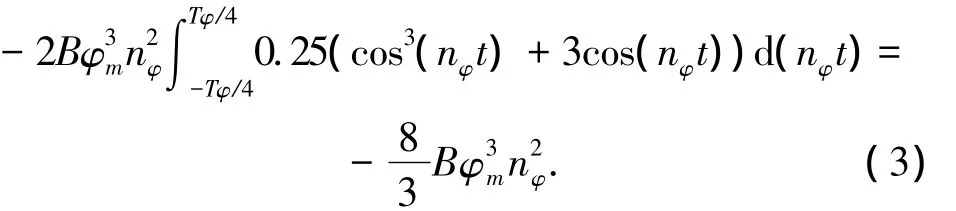
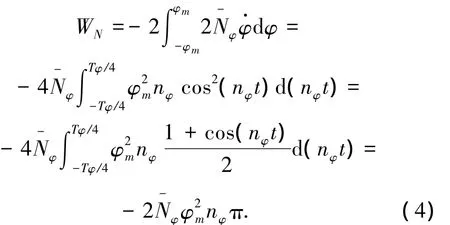
可见等效线性化得阻尼系数与横摇角的幅值呈正比，知道了平方阻尼系数后，可用式(5)求得.通常，平方阻尼系数B可用经验公式近似.

1.2 横摇阻尼系数近似公式

1)贝尔登公式.

这种方法是从平方阻尼公式转化而来的，等效线性阻尼表达式为

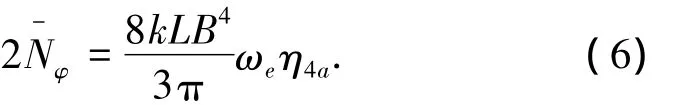
式中:η4a为横摇运动幅值;ωe为遭遇圆频率;L、B为垂线间船长、型宽;k为经验系数，根据船型特征确定.

2)米勒法.

米勒等根据军舰模型的静水横摇衰减曲线分析整理，给出平方阻尼的无因次等效线性阻尼系数与船主尺度，舭龙骨长度以及航速相关的近似式:

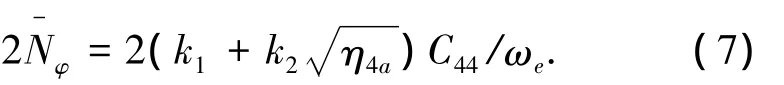
其中:

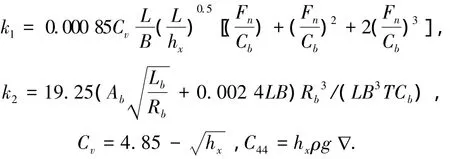
式中:hx为横稳心高，Cb为方形系数，Rb、lb、Ab为舭龙骨参数.

3)驳船经验公式法.

驳船经验公式适用于船体型线较为方整的船舶，其等效线性化的阻尼表达式为

其中:

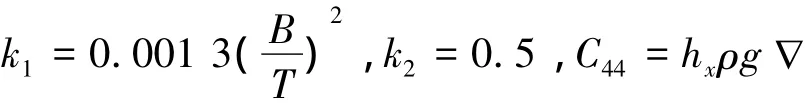
4)临界阻尼系数修正法.

等效线性化的阻尼表达式:

式中:Bcoef为临界阻尼修正系数，通常取0.05;I11为船舶绕纵轴惯性矩;A44为横摇附加质量.

此外，等效线性化得阻尼系数与横摇运动幅值有关，所以求解横摇运动的过程是一个迭代计算的过程，由计算机实现计算.

2 横摇运动修正

根据三维势流理论，船舶在波浪中运动时的总的运动方程为

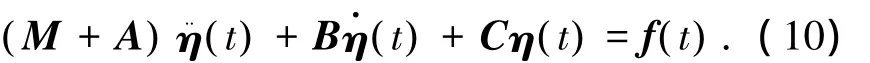
式中:M为船舶质量矩阵;C为静恢复力矩阵;η(t)为船舶6自由度运动列向量;f(t)为波浪干扰力，为波浪主干扰力和波浪绕射力之和.波浪辐射力:

式中，A为附加质量矩阵，B为阻尼系数矩阵，且

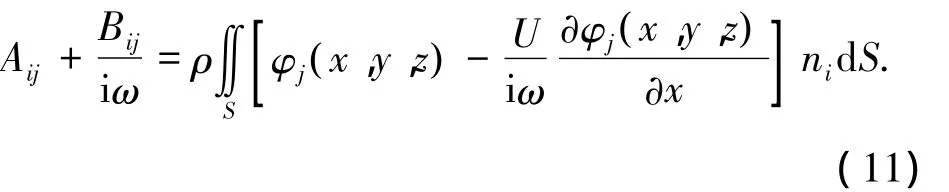
式中，φj(x，y，z)为单位辐射势，在定解条件下运用源汇分布法［12］求解.

针对横摇运动，需要对阻尼系数矩阵中的B44项进行非线性阻尼修正，具体方法是用上述等效线性化后的阻尼系数代替线性阻尼系数，求解横摇运动方程.

本文根据船舶在波浪中横摇的剧烈程度选取4种不同标准船型:散货船、大型浮吊船、集装箱船和Wigley船型.运用上述原理和非线性横摇阻尼系数近似公式，基于三维线性运动与波浪载荷计算程序计算其横摇运动的幅频响应，从而反映各种近似公式对不同船型的修正效果，计算采用1 m和6 m波幅，波浪频率范围 0.1 ～1.8 rad/s，间隔 0.1 rad/s，浪向角取艏斜浪60°.图1为计算船舶水动力模型，表1为计算船舶的主要船型参数.

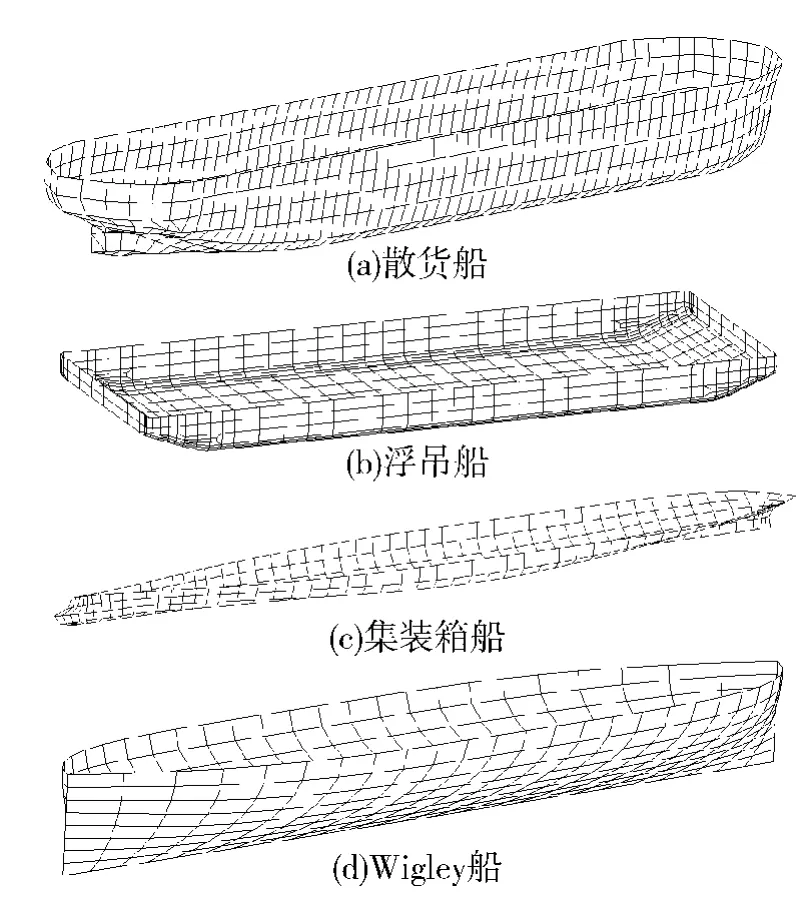
图1 船舶水动力计算模型Fig.1 Hydrodynamic model of the ship

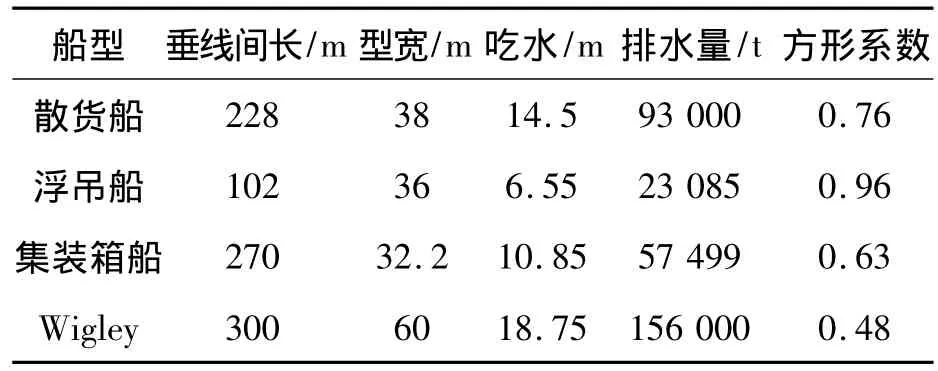
表1 船型参数Table 1 Principal dimensions of the ship

计算结果如图2～5，其中横摇运动幅值响应经过无因次化处理:

分析图2～5可得:

1)由于考虑了非线线横摇阻尼，运用等效线性化方法进行横摇运动修正后，横摇幅值有所下降，且不同经验公式下的修正程度不尽相同.

2)当波幅是1 m时，由于横摇幅度较小，非线性现象不明显，基本体现不出非线性修正效果，但随着波幅的增加，非线性修正效果体现得十分明显，各种修正公式之间差距较大，横摇幅值也随着波幅的增加呈非线性增长.

3)针对所选4种标准船型，各个横摇非线性阻尼系数近似经验公式的修正效果不同，其中临界阻尼系数法和贝尔登法对各船的横摇运动修正程度较小，米勒法修正效果较明显.

4)通过与试验值的比较可以发现，集装箱船采用以舭龙骨原理的米勒法修正效果最好，Wigley船型采用驳船经验公式和米勒法有较好的修正效果.对于散货船和大型浮吊船，米勒法的修正效果最为显著，幅值的变化最大，更能体现横摇非线性效应，但由于缺少试验数据，其工程适用性有待进一步研究.

图2 不同波幅下散货船横摇运动响应Fig.2 Roll response of bulk carrier at different wave am plitudes

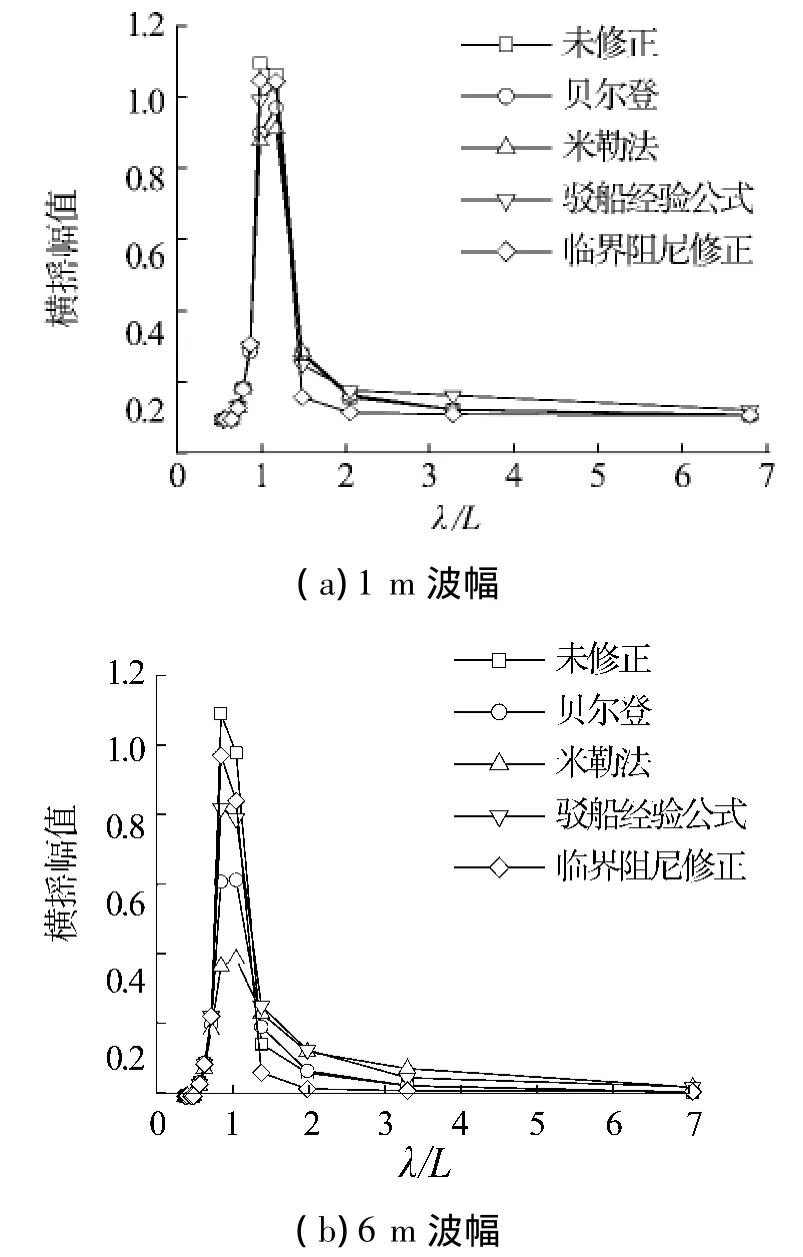
图3 不同波幅下浮吊船横摇运动响应Fig.3 Roll response of floating crane at different wave amplitudes

图4 不同波幅下集装箱船横摇运动响应Fig.4 Roll response of container ship at different wave am plitudes

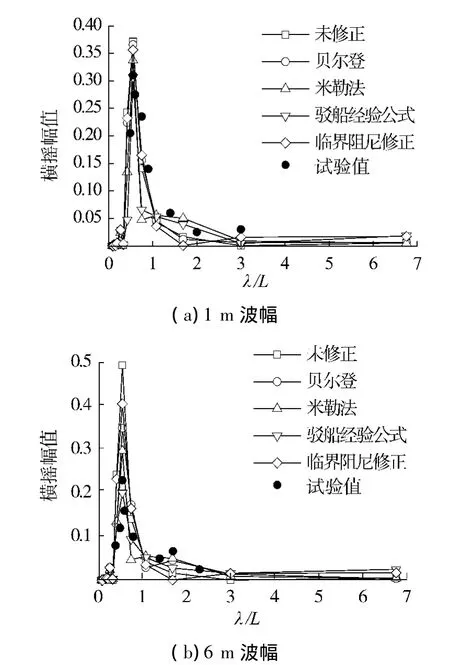
图5 不同波幅下Wigley船横摇运动响应Fig.5 Roll response of Wigley at different wave amp litudes

3 波浪扭矩修正

3.1 问题描述

根据求得的船舶在规则波中的运动稳态解ηj(j=1，2，...，6)和速度势采用线性化的的伯努利方程，并计入静水压力变化部分的贡献，得到总的脉动压力:

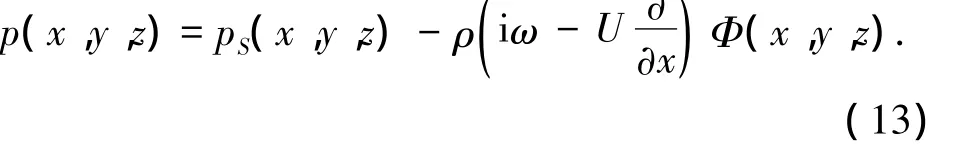
式中:

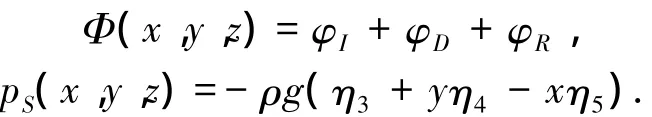
根据达朗伯原理，作用于部分长度船体上的真实流体载荷与刚体惯性力载荷相平衡，可得船体剖面载荷:

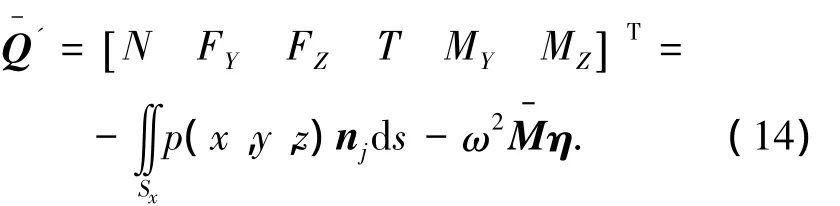
图6 修正前不同频率和浪向下的扭矩分布Fig.6 Distribution of torque at different wave frequencies

扭矩的计算涉及到船体表面脉动压力的积分和横摇运动，上一步在求解横摇运动时，对运动方程中的阻尼系数B44进行了非线性修正，但是脉动压力的求解还是根据线性化理论求得，并未考虑横摇非线性的影响，如式(11)所示，线性化的阻尼系数与式中的辐射势相对应.因此，扭矩的求解会因为只考虑了运动单一方面的非线性横摇修正使方程不封闭，导致扭矩沿船长的分布在船艏处发散.

为了形象地反映该问题，用上述方法计算了某大型浮吊船的扭矩分布，计算时使用米勒法经验公式来近似非线性横摇阻尼，取斜浪和横浪状态，3 m波幅，选取波浪圆频率 ω =0.2，0.6 rad/s，结果如图6所示，其中扭矩采用无因次形式，可见扭矩在船艏处有明显的发散.

3.2 修正方法

为了解决上述扭矩发散的问题，从微观和宏观2个角度分析:

1)微观角度.为了使船体表面脉动压力考虑非线性横摇的影响，本质上需要从速度势入手，基于线性假设的速度势定解条件中需考虑非线性横摇的作用，使得这个问题变得非常复杂.此外，不考虑速度势的修正，直接从修正脉动压力入手，使脉动压力计入阻尼力矩的影响，需要调整每个面元上的脉动压力，但工作量较大且容易出错.

2)宏观角度.由于脉动压力未计入非线性横摇阻尼的影响，致使扭矩在船艏发散.既然对每个面元的脉动压力修正存在困难，可以采用整体修正的方法，即在各个剖面的扭矩计算结果中直接计入非线性横摇阻尼力矩的修正.

通过分析采用宏观修正方法比较合理.应用等效线性化的横摇阻尼系数和线性阻尼系数B44计算出全船受到的横摇阻尼力矩中的非线性部分

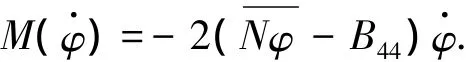
如何正确地将横摇阻尼力矩的非线性部分分配到各个剖面是修正的关键.本文认为每个面元受到的非线性横摇阻尼与其面积有关，因此在宏观上，可以根据湿表面积的大小来分配每个剖面受到的横摇阻尼力矩.剖面离船尾越远，所占的湿表面积越大，则分配到的阻尼力矩也就越大.因此，在这里采用的湿表面积插值分配法，即按照各个剖面到船尾所占湿表面积的比例大小分配非线性横摇阻尼力矩，从而在波浪扭矩的计算中考虑了非线性横摇阻尼的影响.

3.3 结果验证

对于湿表面积插值法原理，本文通过上述大型浮吊船来验证.计算时取浪向角60°和90°，3 m 波幅，选取波浪圆频率 ω =0.2，0.6，1.2 rad/s.计算结果见图7.从图中可以看到，经过上述方法修正后，扭矩在船艏不再出现发散现象，接近封闭，且并没有对其在其他位置的分布造成太大影响，从而有效地在波浪扭矩计算中考虑了非线性横摇阻尼的影响.

图7 修正后不同频率和浪向下的扭矩分布Fig.7 The distribution of torque at differentwave frequencies and wave headings after correction

4 结论

本文基于三维线性势流理论对船舶在波浪中的横摇运动和受到的波浪扭矩进行了全面的横摇非线性修正，得到以下结论:

1)采用等效线性化方法计算得到的非线性横摇阻尼系数可以有效地反映横摇非线性效应，将其运用在运动方程中，可以更加真实准确地预报船舶的横摇运动.本文计算得到了各种非线性横摇阻尼选取方法对横摇运动的影响，为多种船型的横摇运动计算提供了工程指导意见.

2)本文提出的湿表面积插值法，可以在船舶运动求解后的扭矩计算中有效地计入非线性横摇阻尼的影响，解决了由于非线性横摇阻尼在运动和波浪载荷计算时的不统一而造成的波浪扭矩不封闭问题，使横摇的非线性效应在船舶运动和波浪载荷预报中得到完整地体现.

［1］戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京:国防工业出版社，2007:62-64.DAIYishan，DUAN Wenyang.Potential flow theory of ship motions in waves［M］.Beijing:National Defense Industry Press，2007:62-64.

［2］冯铁成.船舶摇摆与操纵［M］.北京 :国防工业出版社，1980:46.

［3］NAYFEH A H，SANCHEZ N E.Stability and complicated rolling responses of ships in regular beam seas［J］.International Shipbuilding Press，1990，37(410):331-352.

［4］胡开业.船舶在波浪中的非线性横摇运动及其稳定性分析［D］.哈尔滨:哈尔滨工程大学，2006:16-22.HU Kaiye.Analysis of nonlinear rolling and stability of a ship in waves［D］.Harbin:Harbin Engineering University，2006:16-22.

［5］李浩，陆建辉.船舶非线性横摇运动方程的线性化研究［J］.船舶，2011，22(5):1-4.LIHao，LU Jianhui.On linearization of ship’s nonlinear rollmotion equation［J］.Ship ＆ Boat，2011，22(5)，1-4.

［6］EISSAM，EI-BASSIOUNY A F.Analytical and numerical solutions of a non-linear ship rolling motion［J］.Applied Mathematics and Computations，2003，34(2):243-270.

［7］李远林，伍晓榕.非线性横摇阻尼的试验确定—数据处理方法［J］.华南理工大学学报:自然学科版，2003，30(2):79-82.LI Yuanlin，WU Xiaorong.Experimental determination of nonlinear roll damping:a technique for data processing［J］.Journal of South China University of Technology:Natural Science Edition，2003，30(2):79-82.

［8］BASS D W，HADDARA M R.Nonlinear Models of Ship Roll Damping［J］.ISP，1998，35(401):5-24.

［9］李积德.船舶耐波性［M］.哈尔滨:哈尔滨工程大学出版社，2001:80-98.LIJide.Ship seakeeping performance［M］.Harbin:Harbin Engineering University Press，2001:80-98.

［10］JOURNEE JM J.Theoretical Manual of SEAWAY［S］.Delft University of Technology Shipydromechanic Laboratory，2001:148-153.

［11］TAYLANM.The effect of nonlinear damping and restoring in ship rolling［J］.Ocean Engineering，2000，27(9):921-932.

［12］戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京:国防工业出版社，2007:23-35.