求解二层线性规划问题的交互式人工蜂群算法

张 涛 (长江大学信息与数学学院，湖北 荆州 434023 水资源与水电科学国家重点实验室(武汉大学)，湖北 武汉 430072)

陈 忠，吕一兵 (长江大学信息与数学学院，湖北 荆州 434023)

求解二层线性规划问题的交互式人工蜂群算法

张 涛 (长江大学信息与数学学院，湖北 荆州 434023 水资源与水电科学国家重点实验室(武汉大学)，湖北 武汉 430072)

陈 忠，吕一兵 (长江大学信息与数学学院，湖北 荆州 434023)

基于人工蜂群算法提出了一种求解二层线性规划问题的交互式人工蜂群算法, 即将求解二层规划问题转化为交互求解下层单目标规划问题和上层单目标规划问题。数值试验表明,该算法能够在较短的时间内得到问题的近似最优解,说明该算法是一种求解二层线性规划问题的有效方法。

人工蜂群算法；线性二层规划；交互式

二层规划问题是一类递阶优化问题,它具有2个决策层, 2个决策层分别有各自的目标函数和约束条件。进行决策时,上层决策者首先根据自己的目标给定一个决策,下层决策者根据上层决策者的决策进行自身目标决策, 并将最优决策反馈到上层,上层决策者再根据下层的反馈修正自己的决策,最终找到使上层目标达到最优的决策。

二层规划模型的求解十分困难,原因之一就是由于双层规划问题是一个NP-难问题。即使是很简单的二层线性规划问题也是NP-难问题,不存在多项式求解算法[1]。二层规划的非凸性也是造成二层规划问题求解异常复杂的另一重要原因。目前，国内外一些学者提出的求解算法或求解方法,但大多数都是针对特定的二层规划模型提出的。设计求解二层规划算法的主要难点在于：上层问题的可行解一定是下层问题的最优解。这就要求只能将下层问题的精确最优解反馈给上层。大量实践表明，下层问题的近似最优解通常可以作为最优响应反馈给上层，从而通过上层问题的求解得到整个问题的近似最优解，然后再通过预设的迭代次数，可以使整个问题的近似最优解任意精度的逼近精确解[2]。为此，笔者基于人工蜂群算法提出了一种求解二层线性规划问题的交互式人工蜂群算法。

1 线性二层规划模型

假设x∈X⊂Rn,y∈Y⊂Rm,F:X×Y→R,andf:X×Y→R,则线性二层规划可以写为：

(1)

式中，F(x,y)和f(x,y)分别为上层目标函数和下层目标函数；c1,c2∈Rn；d1,d2∈Rm；b1∈Rp；b2∈Rq,A1∈Rp×n,B1∈Rp×m,A2∈Rq×n,B1∈Rq×m。

假设：

S={(x,y)|G(x,y)≥0,g(x,y)≥0}X={x|∃y,G(x,y)≥0,g(x,y)≥0}

S(x)={y|g(x,y)≥0}

定义1固定x∈X, 如果y是下层问题的一个最优Pareto最优解，则(x,y)为问题(1)的可行解。

定义2如果(x*,y*)是问题(1)的可行解, 对于任意的(x,y)∈IR, 都有F(x*，y*)≤F(x,y), 则(x*,y*)是问题(1)的一个最优解。

2 人工蜂群算法

人工蜂群算法是Karaboga提出的一种模仿蜜蜂觅食的新型启发式算法[3]，与遗传、模拟退火、粒子群等算法相比，人工蜂群具有控制参数少、计算简洁、易于实现等优点，且有较好的平衡探索与开发能力，已被越来越多的学者所关注并已成功的应用于解决函数的数值优化问题[4-6]。在优化问题求解时，食物源的位置对应优化问题的可行解，食物源的收益度对应优化问题的适应度值，最大收益度食物源对应优化问题的最优解。

一般地，人工蜂群通过方程(1)随机产生P个解：

(2)

(3)

式中，vij代表在xij附近产生一个新解，k∈{1,2,…,s}，k和j都是随机选取，k是i邻域的一个解，且k≠i；rij∈rand[-1,1]。跟随蜂对解的选择是通过观察引领蜂的摇摆舞来判断解的适应度值，并依据选择概率大小来选择跟随哪个引领蜂。

适应度值fitnesssi和选择概率p计算公式如下：

在人工蜂群算法中，利用参数R来记录某个解被更新的次数。如果某个解连续R次循环后没有得改善，则证明该解陷入局部最优，就要被放弃。假设被放弃的解是xi，则根据邻域构成规则随机产生一个新解来代替原来解xi。人工蜂群算法(算法1)的计算步骤如下：

步1 产生初始解集xij,i=1,2,…,S,j=1,2,…,D。设置triali=0，triali表示非改进解xi的数量。

步3 设置外循环初始值m=1。

步4 设置内循环初始值l=1。

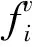
步7 如果解xi没有改进，则triali=triali+1；否则，triali=0。

步9 跟随蜂根据概率pi选择食物源(解)，然后进行领域搜索产生新解，再计算其适应度；转步6～步7。

步10 设置i=i+1。

步11 如果l

步13 所有搜索完毕后，记录当前最好的解。

步14 设置m=m+1。

步15 如果m

3 求解线性二层规划问题的人工蜂群算法

利用人工蜂群算法求解线性二层规划问题,对上下层都采用人工蜂群群算法进行求解。算法(算法2)步骤如下:

步1 根据方程(2)初始化上层决策变量xi,设置i=0，设置i的最大值为P。

步2 求解下层优化问题。固定xi，将xi带入到问题(1)的下层，利用算法1求解下层问题的最优解y*。

步3 求解上层优化问题。将步2中的y*反馈到上层，利用算法1求解上层问题的最优解x及最优值F。令x*=x,y*=y,F*=F。

4 试验仿真与结果分析

算例1[7]设x∈R,y∈R,考虑如下线性二层规划问题：

算例2[8]设x∈R2,y∈R3，考虑如下线性二层规划问题：

根据算法2，利用c#进行编程，算法中的具体参数设置如下：算法1中种群S=100，内层循环次数l=40，外层循环次数m=80; 算法2中，p=50，最后得出的结果与文献的结果比较见表1。从数值试验结果来看,利用笔者所设计算法的计算结果与最优解的误差很小，因此，该算法是有效的。数值试验还表明，人工蜂群算法对种群规模要求不是很大，节约了计算时间。

表1 仿真结果

[1]Bard J. Some properties of the bi-level linear programming[J]. Journal of Optimization Theory and Applications, 1991, 32: 146-164.

[2] Zhang T, Hu T S，Zheng Y.An Improved Particle Swarm Optimization for Solving Bilevel Multiobjective Programming Problem[J]. Journal of Applied Mathematics, doi:10.1155/2012/626717, 2012.

[3]Karaboga D, Basturk B.A powerful and efficient algorithm for numerical function optimization：artificial bee colony (ABC) algorithm[J].Journal of Global Optimization, 2007, 39(3):459-471.

[4]罗钧，李研.具有混沌搜索策略的蜂群优化算法[J].控制与决策，2010,25(12):1913-1916.

[5]胡珂，李迅波，王振林.改进的人工蜂群算法性能[J].计算机应用, 2011,31(4):1107-1110.

[6]王慧颖，刘建军，王全洲.改进的人工蜂群算法在函数优化问题中的应用[J].计算机工程与应用，2011,7(13)：36-39..

[7]Anandalingam G， White D J. A solution method for the linear static stackelberg problem using penalty functions [J]. IEEE Transaction on Automatic Control, 1990,35(10):1170-1173.

[8]Bard J F. Partical Bilevel optimization Algorithm and Applications [M]. Kluwer Academic Publishers, USA, 1998.

2012-10-25

国家自然科学基金项目(11201039；61273179)；湖北省教育厅重点项目(D20101304)。

张涛(1978-)，男，讲师，博士生，现主要从事复杂系统建模与智能计算方面的教学与研究工作。

O221.1

A

1673-1409(2013)01-0001-03

[编辑] 洪云飞