几个最值问题的再思考

●

(奉化高级中学 浙江奉化 315500)

几个最值问题的再思考

●罗永高

(奉化高级中学 浙江奉化 315500)

文献[1]给出了3个最值问题：

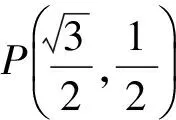
(1)略；

(2)求|OM|+|ON|-|MN|的最大值.

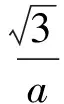
作者用纯粹的代数方法，并巧施待定系数法构造柯西模型展示了3个相关问题的初等解法.细心的读者不难发现，3个问题均蕴含几何意义，能否运用几何意义来解答上述3个问题呢？

1 化归问题

过点P(4,8)任作一条直线分别交x轴、y轴的正半轴于点M(a,0),N(b,0)，求Rt△OMN中直角所对旁切圆半径的2倍的最小值.

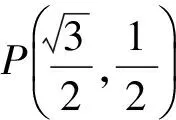
2 问题解决

2.1 问题1的解答

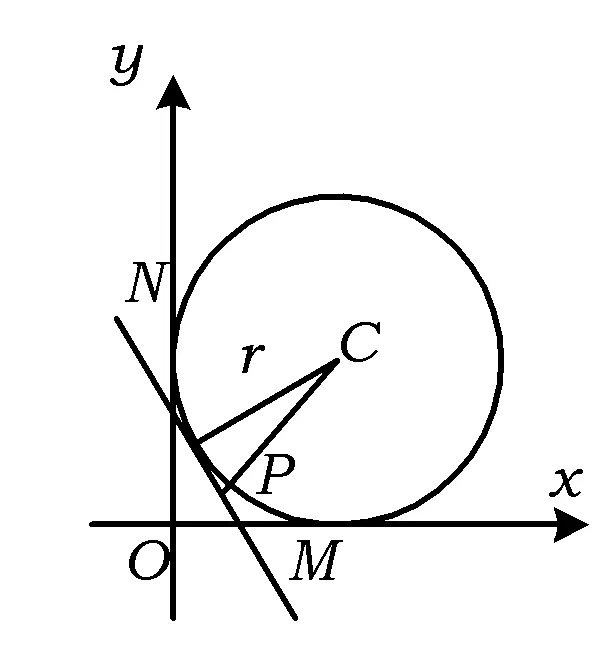
图1

解如图1，设△OMN中直角所对旁切圆的圆心为C,令旁切圆的半径为r,则点C的坐标为(r,r).因为|CP|≥r,所以

(r-4)2+(r-8)2≥r2,

即

r2-24r+80≥0,

解得r≥4或r≥20.显然r≥4不符合条件，舍去.

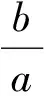
2.2 一般情形

运用上述方法，可得以下一般情形:

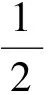
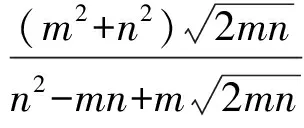
同样可得问题2与问题3的一般情形：

定理2过定点P(m,n)(m>0,n>0)的直线l交x轴的正半轴于点M,交y轴的正半轴于点N,O为坐标原点.令|OM|=a,|ON|=b,Rt△OMN内切圆的半径为r,则

证明如图2，设△OMN内切圆的圆心为C,令内切圆的半径为r,则点C的坐标为(r,r).因为|CP|≥r,所以

(r-m)2+(r-n)2≥r2,

即

r2-(2m+2n)r+m2+n2≥0,

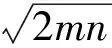
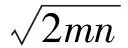
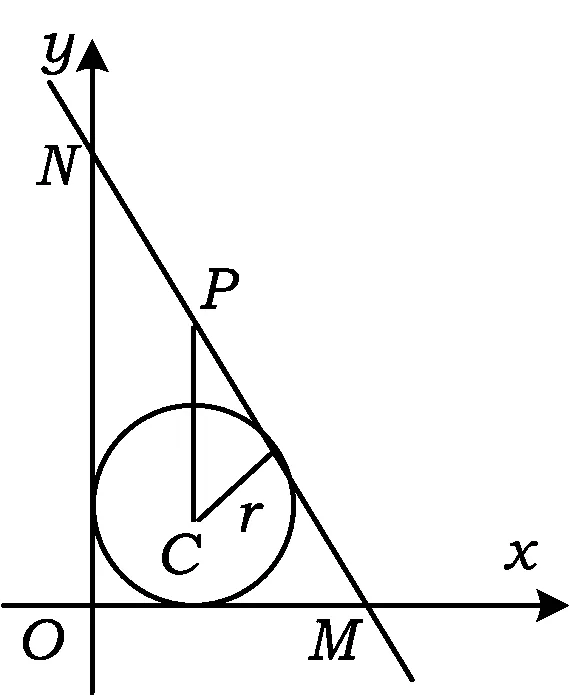
图2

从而

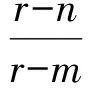
解得

从而

得

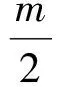
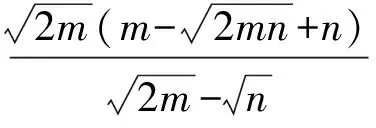
点评解决上述问题除了发现|CP|≥r以外，还需要对内切圆存在的条件进行分析，只有当kCP>0时，内切圆存在，否则内切圆不存在.

3 进一步推广

问题4过定点P(m,n,p)(m>0,n>0,p>0)的平面α交x轴的正半轴于点A,交y轴的正半轴于点B,交z轴的正半轴于点C,O为坐标原点.令|OA|=a,|OB|=b,|OC|=c,三棱锥O-ABC的内切球半径为r,求内切球半径的最大值.

解如图3，设内切球的球心为M,内切球的半径为r,则M(r,r,r),因为|MP|≥r,所以

(r-m)2+(r-n)2+(r-p)2≥r2，

即

2r2-2(m+n+p)r+m2+n2+p2≥0.

令Δ=4[(m+n+p)2-2(m2+n2+p2)]=4(2mn+2mp+2np-m2-n2-p2).

(1)当Δ≤0,即m2+n2+p2≥2mn+2mp+2np时，

2r2-2(m+n+p)r+m2+n2+p2≥0

对任意的r恒成立，因此r没有最值.

(2)当Δ>0,即m2+n2+p2<2m+2mp+2np时，

图3

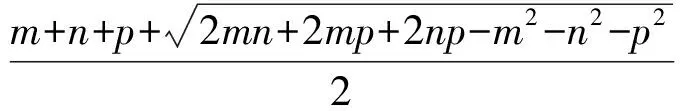
(m-r)∶(n-r)∶(p-r)=bc∶ac∶ab,

从而

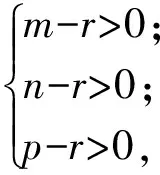
即

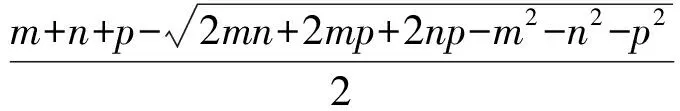
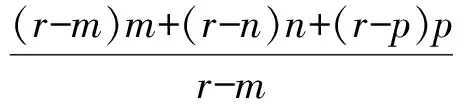
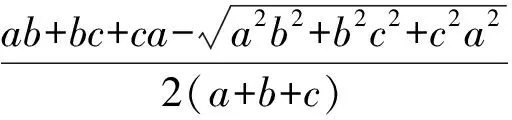
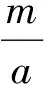
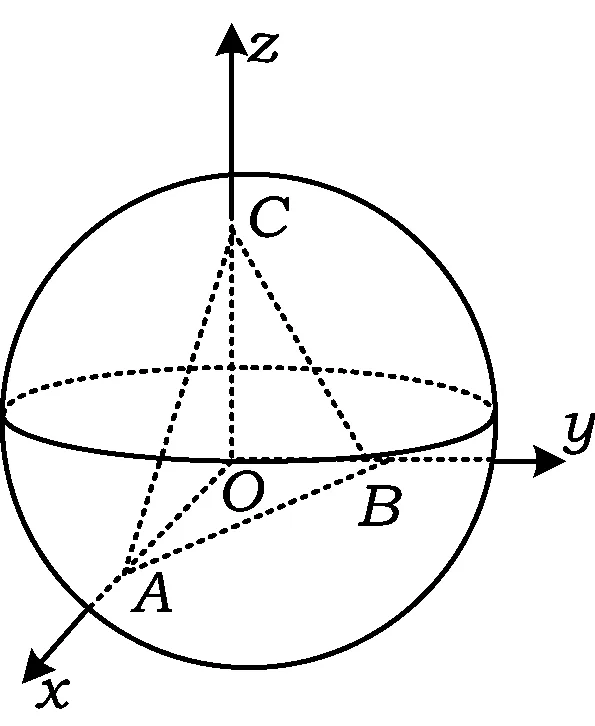
图4

问题5过定点P(m,n,p)(m>0,n>0,p>0)的平面α交x轴的正半轴于点A,交y轴的正半轴于点B,交z轴的正半轴于点C,O为坐标原点.令|OA|=a,|OB|=b,|OC|=c,三棱锥O-ABC的顶点O所对旁切球的半径为r,求旁切球半径的最小值.

解如图4，设旁切球的球心为M,半径为r,则点M的坐标为(r,r,r).因为|MP|≥r,所以

(r-m)2+(r-n)2+(r-p)2≥r2，

即

2r2-2(m+n+p)r+m2+n2+p2≥0.

令Δ=4[(m+n+p)2-2(m2+n2+p2)]=4(2mn+2mp+2np-m2-n2-p2).

(1)当Δ≤0,即m2+n2+p2≥2mn+2mp+2np时，

2r2-2(m+n+p)r+m2+n2+p2≥0

对任意的r恒成立，因此r没有最值.

(2)当Δ>0,即m2+n2+p2<2mn+2mp+2np时，

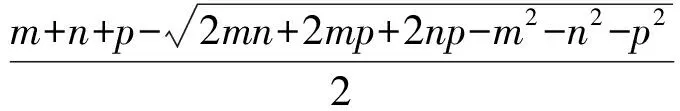
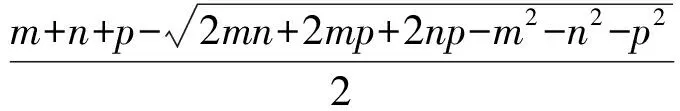
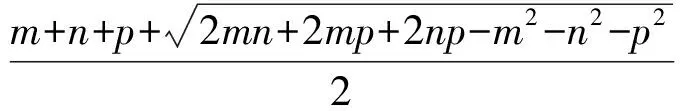
因此,当m,n,p满足m2+n2+p2<2mn+2mp+2np时，旁切球的半径有最小值，最小值为

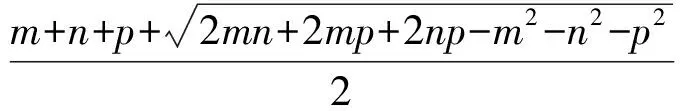
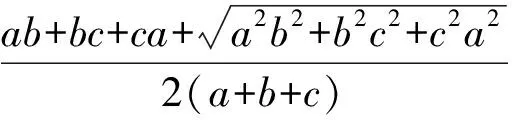
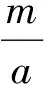
以上通过对每个问题的几何意义进行分析：首先从图形中找到不等关系；然后分析最值取得的条件，使问题的解答变得直观易懂，易于洞察问题的本质.尽管探求过程充满艰辛，但又一次让人体验到“数缺形时少直观，形缺数时难入微”.只有数形结合，数学才会展现出其艺术魅力.

[1] 李建潮.关于几个最值问题的研究[J].中学教研(数学),2013(1):39-41.