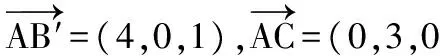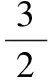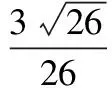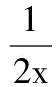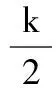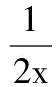2013年数学高考模拟卷(二)

2013年数学高考模拟卷(二)

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的4个选项中，只有一项是符合题目要求的.

1.已知U为全集，A,B,I都是U的子集，且A⊆I,B⊆I，则CI(A∩B)=

( )

A.{x∈U|x∉A且x∉B} B.{x∈U|x∉A或x∉B}

C.{x∈I|x∉A且x∉B} D.{x∈I|x∉A或x∉B}

图1

2.执行如图1所示的程序框图，输出的T的值为

( )

A.12 B.20 C.30 D.42

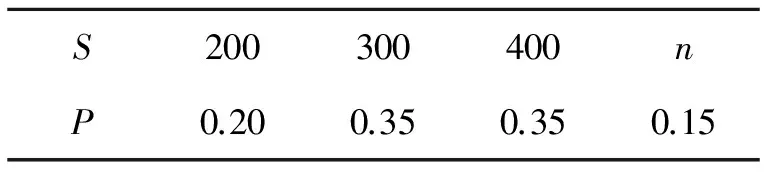
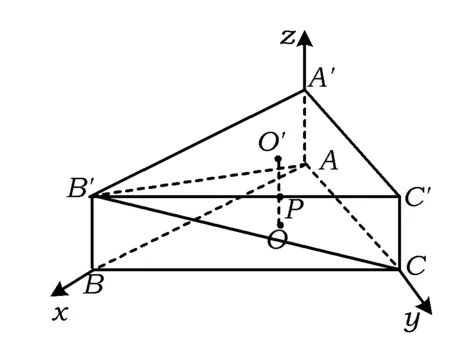
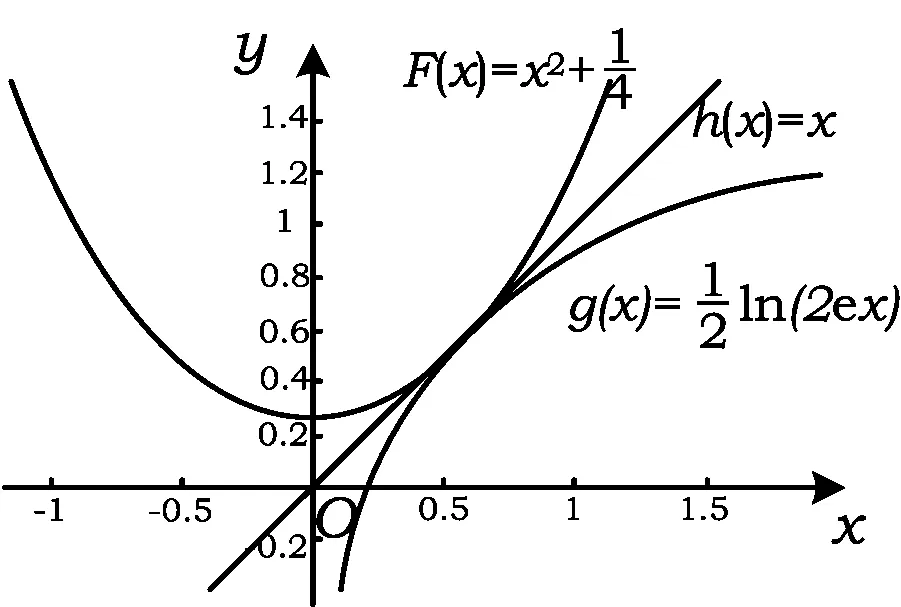
3.等比数列{an}中，a1>0，则“a1

( )

A.充分而不必要条件 B.必要而不充分条件

C.充要条件 D.既不充分也不必要条件

4.已知点A(cos10°,sin10°),B(sin40°,cos40°)，则直线AB的倾斜角等于

( )

A.135° B.120° C.105° D.95°

5.已知m是平面α的一条斜线，点A∉α，l为过点A的一条动直线，那么下列情形可能出现的是

( )

A.l⊥m,l∥αB.l∥m,l⊥αC.l⊥m,l⊥αD.l∥m,l∥α

6.(理)对任意复数x+yi(x,y∈R)，i为虚数单位，定义f(x+yi)=(x+y)+(x-y)i，则对于复数z=a+bi(a,b∈R)，下列结论不正确的是

( )

(文)设i为虚数单位，则下列运算结果不是纯虚数的是

( )

7.已知△OAB的3个顶点坐标分别是O(0,0),A(1,1),B(2,0),直线ax+by=1与线段OA,AB都有公共点，则对于2a-b下列叙述正确的是

( )

图2

A.有最大值而无最小值 B.有最小值而无最大值

C.既有最大值也有最小值 D.既无最大值也无最小值

8.(理)如图2，在正方体ABCD-A′B′C′D′中，M为BC边的中点，点P在底面A′B′C′D′和侧面CDD′C′上运动并且使∠MAC′=∠PAC′，那么点P的轨迹是

( )

A.2段圆弧 B.2段椭圆弧 C.2段双曲线弧 D.2段抛物线弧

(文)如图2，在边长为2的正方体ABCD-A′B′C′D′中，M为BC边的中点，点P在底面A′B′C′D′和侧面CDD′C′上运动并且使AM=AP，那么点P的轨迹长度等于

( )

9.(理)在△ABC中，内角A,B,C所对边长为a,b,c(其中c为常数)，满足a2+b2=2c2，那么当△ABC面积最大时角C的值为

( )

(文)在△ABC中，内角A,B,C所对边长为a,b,c，满足a2+b2=2c2，如果c=2，那么△ABC的面积等于

( )

A.tanAB.tanBC.tanCD.以上都不对

10.已知f(x)是定义在[a,b]上的函数，其图像是一条连续的曲线，且满足下列条件：f(x)的值域为G，且G⊆[a,b]；对任意x,y∈[a,b]，且x≠y,都有|f(x)-f(y)|<|x-y|.那么，关于x的方程f(x)=x在区间[a,b]上根的情况是

( )

A.可能没有实数根 B.有且仅有1个实数根

C.恰有2个实数根 D.可能有无数多个实数根

图3

二、填空题：本大题共7小题，每小题4分，共28分．

(文)某工厂对一批元件进行了抽样检测，根据抽样检测后的元件长度(单位：mm)数据绘制了频率分布直方图(如图3)．若规定长度在[97，103)内的元件是合格品，则根据频率分布直方图估计这批产品的合格品率是______．

12.如图4,△ABC与△ACD都是等腰直角三角形,且AD=DC=2,AC=BC,平面DAC⊥平面ABC,如果以ABC平面为水平面,正视图的观察方向与AB垂直,则三棱锥D-ABC左视图的面积为______.

图4

13.(理)编号为1～8的8个小球按编号从小到大顺序排成一排，涂上红、白2种颜色，5个涂红色，3个涂白色，求恰好有3个连续的小球涂红色，则涂法共有______种.

(文)编号为1～4的4个小球按编号从小到大顺序排成一排，其中2个涂红色，另2个涂白色，求涂红色的2个小球不相邻的概率等于______.

14.(理)首项a1=1的等差数列{an}，其前n项和为Sn，对于一切k∈N*，总有Sk2=(Sk)2成立，则an=______.

(文)函数y=cos2x+2cosx的最小值等于______.

图5

17.(理)实数a>b>c且a+b+c=1，a2+b2+c2=1，则c的取值范围为______.

(文)实数a>b>c且a+b=1-c，a·b=c(c-1)，则c的取值范围为______.

三、解答题：本大题共5小题，共72分，解答应写出文字说明、证明过程或演算步骤．

(1)若BC边长等于1，求θ的值(只需写出(0,2π)内的θ值)；

(2)若θ恰好等于内角A，求此时内角A的大小.

19.(14分)(理)某种鲜花进价每束2.5元，售价每束5元，若卖不出，则以每束1.6元的价格处理掉.某节日需求量X(单位：束)的分布列如表1所示.

表1 X的分布列

(1)若进鲜花400束，求利润Y的均值.

(2)试问：进多少束花可使利润Y的均值最大？

(文)设数列{an}的前n项和为Sn，已知Sn=2an-3n(n∈N*)，

(1)求数列{an}的通项公式an.

(2)问数列{an}中是否存在某3项，它们可以构成一个等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由.

20.(14分)(理)如图6，△ABC的3条边长分别为AC=6,AB=8,BC=10,O′为其内心；取O′A,O′B,O′C的中点A′,B′,C′，并按虚线剪拼成一个直三棱柱ABC-A′B′C′(如图7)，上、下底面的内心分别为O′与O.

(1)求直三棱柱ABC-A′B′C′的体积；

(2)在直三棱柱ABC-A′B′C′中，设线段OO′与平面AB′C交于点P，求二面角B-AP-C的余弦值.

图6 图7 图8

(文)如图8，直三棱柱ABC-A′B′C′中，AA′=1，AB=4,AC=3,BC=5.

(1)求证：AC⊥AB′并说明图中点A,B,C,C′,B′在同一个球面上；

(2)设平面AB′C和平面ABC′的交线为AN，求直线AN和侧面ABB′A′所成角的正弦值.

(1)求轨迹C的方程；

(文)设函数f(x)=x2-x和g(x)=lnx，

(1)求y=f(x)-g(x)(x>0)的最小值.

(2)探究是否存在一次函数h(x)=kx+b使得f(x)≥h(x)且h(x)≥g(x)对一切恒x>0成立.若存在，求出一次函数的表达式;若不存在，说明理由.

(1)求y=f(x)-g(x)(x>0)的最小值；

(2)探究是否存在一次函数h(x)=kx+b使得f(x)≥h(x)且h(x)≥g(x)对一切x>0恒成立.若存在，求出一次函数的表达式，若不存在，说明理由；

(1)求抛物线C的方程.

(3)是否存在垂直于x轴的直线l，使得l被以AT为直径的圆截得的弦长为定值？若存在，求出l的方程；若不存在，请说明理由.

参考答案

1.D 2.C 3.B 4.B 5.A 6.(理)B(文)B

7.D 8.(理)C(文)C 9.(理)C(文)C 10.B

若BC边长等于1，则

(2)因为

所以

即

从而

19.解(理)(1)销售量S(单位：束)的分布列如表2所示.

表2 S的分布列

从而E(S)=325,而Y=3.4Z-360，因此

E(Y)=3.4×325-360=745.

(2)设进n(n≤500)束花，当400

表3 S的分布列

可得E(S)=0.15n+285，从而E(Y)=-0.39n+901.

同理可对其他区间讨论后得

易知，当n=400时，E(Y)取最大值745.

(文)(1)易知a1=3,当n≥2时，

Sn=2an-3n且Sn-1=2an-1-3(n-1)，

两式相减得

an=2an-1+3,

于是

an+3=2(an-1+3)，

从而

an+3=2n-1(a1+3)=3×2n,

即

an=3×2n-3.

(2)设m,k,n∈N*且m

am+an=2ak,

从而

2m+2n=2·2k，

于是

1+2n-m=2k+1-m.

而1+2n-m是奇数，2k+1-m是偶数，假设不成立，因此不存在某3项可以构成一个等差数列.

图9

20.解(理)(1)易知△ABC为直角三角形，且其内切圆半径等于2，于是直三棱柱ABC-A′B′C′的高等于1，体积

可得

n=(0,1,-4).

(文)(1)因为BC2=AB2+AC2，所以AC⊥AB，而AC⊥AA′，从而AC⊥面ABB′A′，故AC⊥AB′；同理可得AB⊥AC′.联结B′C和BC′交于点N，则

因此点A,B,C,C′,B′在以N为球心的球面上.

即

(2)①若l不与y轴重合，设直线l的方程为y=kx+1，代入椭圆C的方程得

(4k2+9)x2+8kx-32=0.

设P(x3,kx3+1),Q(x4,kx4+1),则

设点T(0,t)，则

(1+k2)x3x4+k(1-t)(x3+x4)+(1-t)2=

(文)(1)当x>0时，

当x∈(0,1)时,y′<0，y=f(x)-g(x)递减；当x∈(1,+∞)时,y′>0，y=f(x)-g(x)递增.因此,当x=1时,y=f(x)-g(x)取最小值0.

(2)由第(1)小题易知，f(1)=g(1)=0，所以h(1)=0.

猜测一次函数的图像恰为y=f(x)和y=g(x)在点(1,0)处的公切线，即

h(x)=x-1.

而

f(x)-h(x)=(x-1)2≥0；

G(x)=g(x)-h(x)≤0(证略).

因此f(x)≥h(x)且h(x)≥g(x)对一切x>0恒成立.

22.解(理)(1)当x>0时，

图10

(2)由第(1)小题易知

得

恒成立，于是

Δ=(k-1)2≤0，

得

k=1,h(x)=x.

综上所述，存在h(x)=x符合题目要求，它恰好是y=f(x),y=g(x)图像的公切线.

an=g(an-1)

即{an}为递减数列.因此

(2)设直线AB:x=ny+2,与抛物线方程联立消去x得

y2-4ny-8=0，

因此

y1+y2=4n，y1y2=-8.

设抛物线C上点M(x0,y0)，A(x1,y1)，B(x2,y2),则

(ny1+2-x0)(ny2+2-x0)+(y1-y0)(y2-y0)=

(n2+1)y1y2+(2n-x0n-y0)(y1+y2)+4-

而圆心到直线l的距离

因此l被圆截得的弦长

当m=1时,弦长L=2为定值，此时直线l的方程为x=1.

(供稿人：李金兴)