直线与圆锥曲线综合问题的求解策略
2013-10-26海宁市高级中学浙江海宁314400
● (海宁市高级中学 浙江海宁 314400)
直线与圆锥曲线综合问题的求解策略
●顾贯石(海宁市高级中学 浙江海宁 314400)
解析几何是通过代数方法来研究几何问题的一门学科,它将几何与代数进行完美地结合,有很强的综合性.其中直线与圆锥曲线综合问题是历年高考的重点之一,常以中难题为主,主要涉及:位置关系的判定问题、求值问题(长度、面积等)、求参数的最值与范围问题、定点与定值问题、存在性问题等等.突出考查数形结合、函数与方程、分类讨论、等价转化等数学思想方法,对分析问题和解决问题的能力、运算能力等有较高的要求.
1 典例剖析
直线与圆锥曲线综合问题的求解策略主要有2种:线参数法与点参数法.
1.1 线参数法
所谓“线参数法”,是将条件或结论用坐标(直线与圆锥曲线的交点坐标)表示为x1±x2,x1x2(或y1±y2,y1y2),通过直线方程与圆锥曲线方程联立,用韦达定理或求交点坐标等来求解的方法.其中将条件或结论用坐标表示是线参数法的关键.

图1

(1)当直线l过右焦点F2时,求直线l的方程.
(2)设直线l与椭圆C交于点A,B,且△AF1F2,△BF1F2的重心分别为点G,H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
(2010年浙江省数学高考理科试题)
分析(1)不难求得直线l的方程为
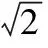
(2)设A(x1,y1),B(x2,y2),则

x1x2+y1y2<0.
联立直线l与椭圆C的方程得到
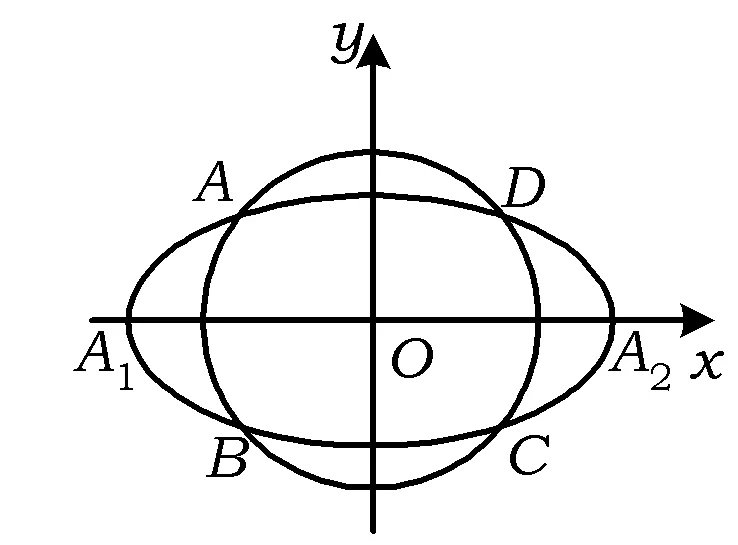
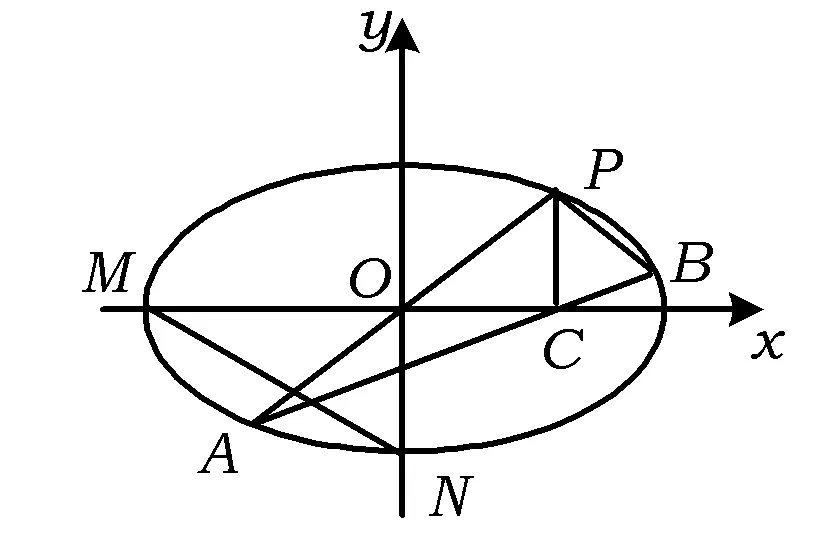
通过韦达定理结合Δ>0,解得m的取值范围为1 图2 (1)求椭圆C的方程. (2)直线l过椭圆C内一点M(m,0),与椭圆C交于点P,Q,点N在直线x=-2上.如果点F恰为△PNQ的垂心,求m的取值范围. λy=x-m. 本题有3个变量m,λ,y0,可以通过“垂心”的条件获得三者关系,从而得到f(m,λ)=0或g(m,y0)=0,再通过求函数值域或解不等式求得m的取值范围. 解由PQ⊥NF,得 即y0=λ. (1) 由NQ⊥PF得 (2) 式(1),式(2)化简得 (λ2+1)y1y2+λ(m+1)(y1+y2)+(m+1)(m+2)=0. (3) (λ2+2)y2+2λmy+m2-2=0. 代入式(3)化简得, mλ2=-(3m2+6m+2)(显然m≠0). 由λ2≠0得 评注本题容易发现:m的变化与l的斜率、点N的纵坐标有关.由“垂心”的条件可转化为f(m,λ)=0来求解,但列出关于坐标的等式(3)是本题的难点.本题主要考查椭圆的几何性质、直线与椭圆、三角形垂心等基础知识,考查解析几何基本思想方法和综合解题能力. 1.2 点参数法 所谓“点参数法”,是根据条件列出相关点坐标的等式,通过对得到的等式进行有目的的变形而求解的方法.但由于列出的等式有时参数较多,如果代数变式基础薄弱、变形目标不明确,有时较难求解问题. 图3 (1)求该椭圆的标准方程. (2011年重庆市数学高考理科试题) (2)若存在,不难知道点P在以F1,F2为焦点的椭圆上,因此目标是求点P的轨迹方程,即寻找x,y的等式.但本题很难通过联立方程组,用线参数法的方法求解. 寻找x,y的等式可转化为寻找关于x1,y1,x2,y2的等式.考虑到点M,N在椭圆上,则 (5) 因为 所以 x1x2+2y1y2=0. (6) 从而x2+2y2= (x1+2x2)2+2(y1+2y2)2= 20+4(x1x2+2y1y2)=20, 即点P在椭圆x2+2y2=20上,从而求解. 评注本题考查椭圆的定义与方程、椭圆的性质等知识,同时综合向量知识应用“点参数法”考查求曲线方程等问题,也考查学生的探究能力.如果按存在性问题常规解题思路设F1,F2坐标求解,很难获得结论.本题选用“点参数法”比“线参数法”更简单,问题是:能否得出式(4),(5),(6)中的5个等式及对于等式的合理变形,这也是“点参数法”的最核心之处. 图4 (1)求直线AA1与直线A2B交点M的轨迹方程. (2012年辽宁省数学高考理科试题) 分析(1)设A(x1,y2),B(x1,-y1),又A1(-a,0),A2(a,0),由直线A1A,A2B的方程及点A或点B在椭圆上,共3个等式消去x1,y1可得M的轨迹方程为 (2)如果设A=(x2,y2),由矩形ABCD与矩形A′B′C′D′的面积相等可得 由点A,A′均在椭圆上得 根据上述3个式子可变形得 图5 (1)当直线PA平分线段MN,求k的值; (2)当k=2时,求点P到直线AB的距离d; (3)对任意k>0,求证:PA⊥PB. (2011年江苏省数学高考试题) A(-μ,-μk),C(μ,0), 得 从而 因此 PA⊥PB. 证法2线参数法.设A(x1,y1),B(x2,y2),则 P(-x1,-y1),C(-x1,0). 从而 因为点A在椭圆上,代入得 即 PA⊥PB. 证法3点参数法.设P(x1,y1),B(x2,y2),则 A(-x1,-y1),C(x1,0). 由点A,C,B共线得 即 由于点A,B在椭圆上,得 代入上式得 kPAkPB=-1, 因此 PA⊥PB. (1)求椭圆方程. (2)如图6,过点(0,-2)的直线l交椭圆于点A,B、交x轴于点P,点A关于x轴的对称点为C,直线BC交x轴于点Q.探究:|OP|·|OQ|是否为常数? 图6 图7 2.如图7,已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M. (1)求点M到抛物线C1的准线的距离. (2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的2条切线,交抛物线C1于点A,B.若过点M,P的直线l垂直于AB,求直线l的方程. (2011年浙江省数学高考理科试题) (1)求椭圆C的方程; (2)求△ABP的面积取最大时直线l的方程. (2012年浙江省数学高考理科试题) 图8 图9 (1)求椭圆E的方程. (2)是否存在定点M,N,使得|PM|+|PN|为定值?若存在,求出M,N点坐标;若不存在,说明理由. 参考答案 令y=0,则 于是 kAB=x1+x2,kPA=x0+x1,kPB=x0+x2. 由PM⊥AB,PA,PB与圆相切分别得 代入式(7)得 (2)解设直线l1,l2斜率分别为m1,m2,设A(x1,y1),B(x2,y2),则 同理可得 由k1+k2=k3+k4,得 m1m2+2=0. 设P(x,y),则 即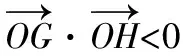

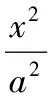
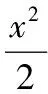
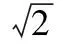
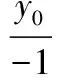



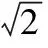

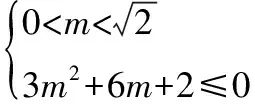


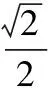











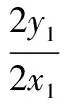
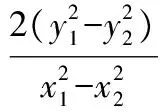

2 精题集萃