C＋＋编程在牛顿环实验误差分析中应用

鞠爱宇，马小程，夏雪琴

（浙江海洋学院，浙江 舟山 316000）

牛顿环是光学中等厚干涉现象的一个典型实例，根据其产生的原理以把它应用在测量凸透镜曲率半径。而实验过程中经常疏忽因中心暗斑直径过大，给测量带来一定误差，影响实验结果。下面通过调节牛顿环中心暗斑大小分别测量曲率半径，再进行误差比较，得到实验时调节适当大小的暗斑直径，能减少实验误差，这为大学物理实验操作提供有利的科学依据。

1 实验原理

在一块平面玻璃上安放上一焦距很大的平凸透镜，使其凸面与平面相接触，在接触点附近就形成一层空气膜。当用一平行的准单色光垂直照射时，在空气膜上、下表面反射的光束相干叠加，形成以接触点为圆心的明暗相间的环状干涉图样，称为牛顿环。其光路示意图如图1［1－2，4－5］。

如果已知入射光波长，并测得第k级暗环的半径rk，则可求得透镜的曲率半径R。但实际测量时，由于透镜和平面玻璃接触时，接触点有压力产生形变或有微尘产生附加光程差，使得干涉条纹的圆心和环级确定困难。用直径Dm、Dn，有

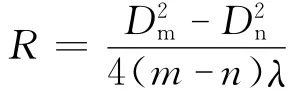
图1 牛顿环及其形成光路图

此为计算R用的公式，它与附加厚光程差、圆心位置、绝对级次无关，克服了由这些因素带来的系统误差，并且Dm、Dn可以是弦长。

不同的中心暗斑大小多次测量，得实验结果也不同，各个曲率半径的相对误差进行比较，就可获得中心暗斑大小对实验测量曲率半径的影响。

2 实验数据记录

表1 凸透镜曲率半径测量数据数据表取mn＝25，λ＝5.893×10 7 m，仪器误差5×10 m，R标 ＝1.038m

表1 凸透镜曲率半径测量数据数据表取mn＝25，λ＝5.893×10 7 m，仪器误差5×10 m，R标 ＝1.038m

暗斑直径mm 组数 环数m XL XR Dm×10 3 m ×10 3 m ×10 3 m XL XR Dn D2m-D2n R 百分差环数n ×10 3 m ×10 3 m ×10 3 m ×10 3 m ×10 3 m %1.486 1 45 25.262 15.722 9.540 20 23.595 18.003 5.592 59.741 1 013.8 2.3 1.686 2 45 25.328 15.751 9.577 20 23.731 18.385 5.346 63.139 1 071.4 3.2 1.842 3 45 25.425 15.792 9.633 20 23.759 18.399 5.360 64.065 1 087.1 4.7 1.908 4 45 25.509 15.806 9.703 20 23.798 18.421 5.377 65.236 1 107.0 6.6_2.924_______5__________45_____25.625__15.846__9.779_____20_____23.991__18.511__5.480__6________________5.598__1_113.2__7.2__

3 C＋＋编程处理实验数据

表1中Dm、Dn、（_）、R、百分差%的运算全部采用C＋＋编程，编写代码小程序，将所测量的实验数据输进去就可得到表1中的计算结果，C＋＋语言程序输出数据界面见图2［3］。

图2 C＋＋语言程序输出数据界面图

C＋＋语言程序代码如下：

4 实验结果与分析

图3 用Excel得到暗斑直径大小与百分差的关系图

在牛顿环实验教学中平凸透镜和平面玻璃接触点的大小是由牛顿环装置三个螺钉所施加的压力来控制。理论上，透镜凸面和平面玻璃应为一点接触，但实际观察牛顿环时会发现，牛顿环的中心并不是一个点，而是一个不太清晰的、或暗或亮的圆斑，是由于重力及压力的作用引起接触处玻璃的形变，使接触点变成一个面所造成的。因此我们观察到的牛顿环中心是一个暗斑。实验时这个暗斑应该调到多大，没有统一规定，这就给测量带来某种程度的不确定性。现在用Excel得到暗斑大小与误差的百分差的关系图3，从图3可知，实验时当暗斑直径在1.5mm左右时，实验测量的百分差在最小区域范围。这为实验调节暗斑的直径大小提供了有利的实验操作科学依据。

［1］ 竺江峰，鲁晓东，夏雪琴.大学物理实验教程［M］.北京：中国水利水电出版社，2011，9.

［2］ 夏雪琴.牛顿环实验数据处理方法的探究［J］.浙江海洋学院学报：自然科学版，2011，7：13－15.

［3］ 钱能.C＋＋程序设计教程［M］.北京：清华大学出版社，2005.

［4］ 王必利.利用牛顿环实验测定玻璃的弹性模量［J］.大学物理实验，2012，04：44－46.

［5］ 用数值计算的方法研究面光源的牛顿环干涉及干涉条纹的可视化［J］.大学物理实验，2013（2）：65－69.