二维表面声源模拟GPS实验算法的讨论

姚赫明，苗明川，Saddam Foad（胡森）

（北京航空航天大学，北京 100191）

模拟GPS实验采用声发射技术的声源定位原理，以声信号传感器模拟定位卫星发射及用户GPS接收机，传感器可接收或发射声波信号，由一个传感器的声发射（AE）信号通过媒质传播到其他多个模拟定位传感器后，转换为电压信号，通过放大得到所需定位时差，通过移动声发射传感器模拟卫星的实际位置［1］，并通过同一个模拟接收机的多组时差计算获得该传感器位置［2］。以声发射技术为基础的GPS模拟实验装置［3］通过理论计算知，媒质中传播的声波可以看作是无频散的表面波，沿表面各方向有相同的速度c。时差测定仪是计时装置，可记下各输入通道收到的传感器输出的电脉冲的时刻，即声波传播到传感器所在点的时间点。

1 实验及数据处理

1.1 实验数据

通过GPS模拟实验进行10次测量，所获实验数据如表1

表1 实验数据

1.2 四种数值算法对数据进行处理

在实验数据的处理过程中，使用matlab程序完成计算，选择的数值方法不同［4］，会得到不同的实验结果。由于不同方法的实现方程组数值收敛的原理不同，对同一组数据会有不同的收敛次数及不同精度［5］。通过比较各组结果，得出适合本实验的最优解法［6］。

1.2.1 牛顿法

（须为非奇异矩阵）选取一组初值

计算得到新的迭代值

重复以上步骤知道d满足精度要求为止。

1.2.2 拟牛顿法

设非线性方程组为

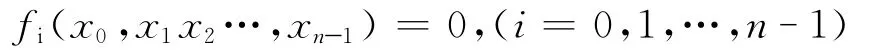
由线性方程组AZ＝B解出

重复计算直到maxB（i）小于所规定的限定条件为止。

1.2.3 蒙特卡洛法

设非线性方程组为

1.2.4 梯度法

设非线性方程组为

定义目标函数为

重复以上步骤直到满足精度要求为止。

1.3 结果示例

以P3（0，0）点为例代入主函数求解得用四种解法得到的最终定位点位置和迭代次数如表2

表2 定位点计算结果

与实际P3（0，0）点比较，四种方法的误差均在实验允许范围内。

2 结 论

从结果可以发现牛顿法与梯度法的迭代次数明显少于拟牛顿法与蒙特卡洛法迭代次数。蒙特卡洛法由于随机数的产生极大影响了收敛的方向与速度，使得此算法对于GPS模拟的计算效果不佳。拟牛顿法计算过程中由于为了避免牛顿法中Jacobi矩阵的偏导数计算，用差商来代替Jacobi矩阵的各偏导数，虽可减少每步的计算量，但每步的收敛速度较慢。而牛顿法梯度法由于计算的直接性，收敛的速度很快，可以达到平方收敛。对于GPS模拟的计算效果很理想。可以看出对于模拟GPS实验的数据处理应选择牛顿法或梯度法。

［1］ J.Lee.Global Positioning／GPS ［J］.International Encyclopedia of Human Geography，2009：548－555.

［2］ 梁家惠，王成云.声源定位实验［J］.物理实验，2000，20（1）：5－7.

［3］ 李朝荣.基础物理实验［M］.北京：北京航空航天大学出版社，2009.

［4］ 王开荣，杨大地.应用数值分析［M］.北京：高等教育出版社，2010.

［5］ 刘寅立，王剑亮.MATLAB数值计算案例分析［M］.北京：北京航空航天大学出版社，2011.

［6］ 范校蜜.对GPS水下远位仪定位的精确性再探究［J］.大学物理实验，2011（5）：7－9.