二阶非线性Schrödinger方程Dirichlet问题的整体W1，2解

宋玉坤，陈 阳，袁洪君

（1.吉林大学 数学研究所，长春130012；2.承德石油高等专科学校 数理部，河北 承德067000）

0 引 言

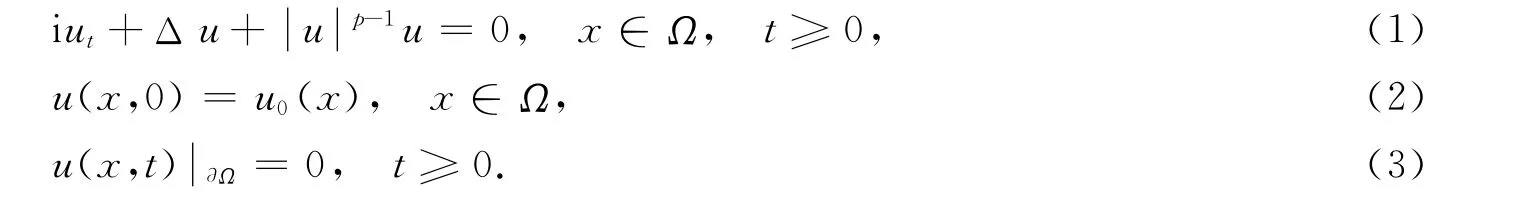
考虑有界域Ω⊂Rn上二阶非线性Schrödinger方程的Dirichlet问题：在物理上，方程（1）描述强激光束通过非均匀介质和等离子体的传播.目前，对不同物理背景下Schrödinger方程整体解的不存在［1－4］与存在性［5－15］研究已有很多结果.

文献［5］研究了一类具非齐项二维方程解的局部和整体适定性；文献［6］利用基态的变分特征、势井和凹性方法给出了类似方程Cauchy问题小初值整体解存在的最佳条件；文献［7－8］研究了方程

本文通过位势井方法结合Sobolev嵌入定理，进一步研究问题（1）－（3），得到了位势井深度d的表达式，并讨论了相关集合在流之下的不变性，得到了解的存在条件，进一步揭示了在位势井内问题（1）－（3）整体解W1，2的存在性.

用‖·‖p表示‖·‖Lp（Ω），‖·‖k，p表示‖·‖Wk，p（Ω），‖·‖＝‖·‖L2（Ω），（u，v）＝∫Ωuvdx.

1 主要结果

引理2 对于u∈W（Ω），‖▽u‖为‖u‖1，2的等价模.

先考虑问题（1）－（3）W1，2解的定义，设u（x，t）是问题（1）－（3）的古典解，用任意的v（x）∈W1，2（Ω）乘以式（1），在Ω上积分，并利用格林公式可得

定义1 若u∈L∞（0，T；W（Ω）），且式（4）对任意的v（x）∈W1，2（Ω）及0≤t≤T 成立，则称u＝u（x，t）为问题（1）－（3）在Ω×［0，T）上的W1，2解.

定义能量泛函：

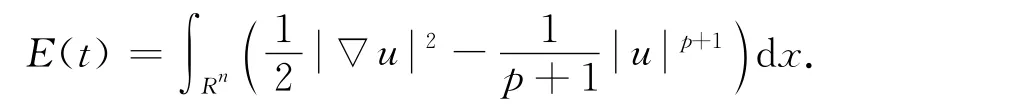
由于问题（1）－（3）不具有正定能量，因此需引入位势井理论，当满足条件（H）时，定义

位势井：

先证明位势井深度d＞0.

证明：由J（u）和I（u）的定义，结合I（u）＝0，‖▽u‖≠0及嵌入定理，有

故

证毕.

定理1 设p满足条件（H），u0（x）∈（Ω）.若0＜E（0）＜d，I（u）＞0或‖▽u0‖＝0，则问题（1）－（3）存 在 一 个 整 体 W1，2解 u（x，t），u∈W，0≤t＜ ∞，且 u∈L∞（0，∞；（Ω）），ut∈L∞（0，∞；L2（Ω））成立.

证明：设｛ωj（x）｝为（Ω）的一个基函数系，构造问题（1）－（3）的近似解：

其中，gjm（t）是［0，T］上的复值函数，且满足如下非线性常微分方程组的初边值问题：

对t从0到t积分得

由E（0）＜d知，J（u0）＜d.再由I（u0）＞0或‖▽u0‖＝0可得，u0∈W.又因为W 是W1，2（Ω）中的开集，因此由式（6）可知，对充分大的m，有

下面证明W 在问题的流之下不变.假设式（8）不成立，则必存在某个t0＞0及充分大的m，使得um（t）∈∂W，即

由式（7）可得，对充分大的m，有J（um）＜d，故J（um（t0））＝d不可能.若

则显然有J（um（t0））≥d，这与式（8）矛盾，即对于充分大的m，有um（t）∈W.又由式（6）可得

从而

由于｛ws｝在W1，2（Ω）中稠密，故由式（9）可得式（4）成立.又由式（6）可得u（x，0）＝u0（x）.所以u（x，t）是问题（1）－（3）在Ω ×［0，∞）上的整体W1，2解.

［1］Glassy R T.On the Blowing up of Solutions to the Cauchy Problem for Nonlinear Schrödinger Equations［J］.J Math Phys，1977，18（9）：1794－1797.

［2］Takayoshi Ogawa，Yoshio Tsutsumi.Blow up of H1Solutions for the One－Dimensional Nonlinear Schrödinger Equations with Critical Power Nonlinearity［J］.Proc Amer Math Soc，1991，111（2）：487－496.

［3］Takayoshi Ogawa，Yoshio Tsutsumi.Blow up of Solutions for the Nonlinear Schrödinger Equation with Quartic Potential and Periodic Boundary Condition ［C］／／Functional－Analytic Methods for Partial Differential Equations Lecture Notes in Mathematics.Vol.1450.［S.l.］：Springer，1990：236－251.

［4］ZHANG Jian，LI Xiao－guang，WU Yong－hong.Remarks on the Blow－up Rate for Critical Nonlinear Schrödinger Equation with Harmonic Potential［J］.Applied Mathematics and Computation，2009，208（2）：389－396.

［5］Ginibre J，Velo G.On a Class of Nonlinear Schrödinger Equations.Ⅰ.The Cauchy Problem，General Case［J］.J Funct Anal，1979，32（1）：1－32.

［6］SHU Ji，ZHANG Jian.Sharp Conditions of Global Existence for a Class of Inhomogeneous Nonlinear Schrödinger Equations［J］.Acta Mathematicae Applicatae Sinica，2009，32（2）：193－199.（舒级，张健.一类具非齐次项的非线性Schrödinger方程整体解存在的最佳条件 ［J］.应用数学学报，2009，32（2）：193－199.）

［7］Lange H.On Nonlinear Schrödinger Equations in the Theory of Quantum Mechanical Dissipative Systems［J］.Nonlinear Analysis，1985，9（10）：1115－1133.

［8］GUO Bo－ling，XING Jia－sheng.On Nonlinear Schrödinger Equations with Harmonic Oscillator ［J］.Acta Mathematicae Applicatae Sinica，2001，24（4）：554－560.（郭柏灵，邢家省.具调和振子的非线性Schrödinger方程 ［J］.应用数学学报，2001，24（4）：554－560.）

［9］SHU Ji，ZHANG Jian.Nonlinear Schrödinger Equation with Harmonic Potential［J］.Journal of Mathematical Physics，2006，47（6）：063503.

［10］SONG Yu－kun，CHEN Yang.The Global Solutions of Cauchy Problem for a Class of Schrödinger Equations［J］.Journal of Natural Science of Heilongjiang University，2008，25（2）：253－255.（宋玉坤，陈阳.一类Schrödinger方程的Cauchy问题的整体解 ［J］.黑龙江大学自然科学学报，2008，25（2）：253－255.）

［11］Ozawa T.Finite Energy Solutions for the Schrödinger Equations with Quadratic Nonlinearity in One Space Dimension［J］.Funkcialaj Ekvacioj，1998，41（3）：451－468.

［12］Chabrowski J，Szulkin A.On the Schrödinger Equation Involving a Critical Sobolev Exponent and Magnetic Field［J］.Topological Methods in Nonlinear Analysis，2005，25（1）：3－21.

［13］DING Yan－heng，LIN Fang－hua.Solutions of Perturbed Schrödinger Equations with Critical Nonlinearity ［J］.Calculus of Variations，2007，30（2）：231－249.

［14］ZHANG Hui－xing，LIU Wen－bin.Existence of Solutions of Perturbed Schrödinger Equation Involving a Critical Nonlinearity and Magnetic Fields ［J］.Journal of Jilin University：Science Edition，2012，50（2）：227－231.（张慧星，刘文斌.带有磁势和临界增长的薛定谔方程解的存在性 ［J］.吉林大学学报：理学版，2012，50（2）：227－231.）

［15］YE Yao－jun.The Global Small Solutions for a Class of Nonlinear Schrödinger Equation［J］.Acta Mathematicae Applicatae Sinica，2006，29（1）：91－96.（叶耀军.一类非线性Schrödinger方程的整体小解 ［J］.应用数学学报，2006，29（1）：91－96.）