基于混合算法的大坝变形预测分析
2013-10-24周密
周 密
( 中国南方电网调峰调频发电公司 天生桥水力发电总厂,贵州 兴义562400)
0 引 言
我国水能资源丰富,水资源分布却极不平衡,为了开发利用水能资源和解决垮流域供水问题,我国自建国以来兴建了将近9 万座大坝,这些大坝不仅在防洪、灌溉、水力发电、水路航运和城市供水等方面发挥着重要作用,同时对流域生态环境改造等方面也有着重要影响。由于大坝在运行过程中,受到水压力、温度、当地环境等多种因素影响会产生变形,该变形在时间上具有明显的时效性,是一种复杂的非线性变化。一旦大坝变形超过了设定范围,将直接影响到大坝自身安全,进而对周围工农业生产和人类生活活动造成极大的威胁。因此,开展大坝自动检测与趋势预测,一直都是水利水文工作者的研究热点之一[1-2]。
近年来,由于自动化水平的提高以及逐步回归分析、神经网络、小波分析等函数逼近与预测算法的发展,大坝变形预测也得到了较快的发展。比如黄世秀等[3]针对港口湾大坝实测数据,采用BP 神经网络模型进行大坝变形预测,获得了有效的预测值,进一步研究了大坝变化规律; 朱金海等[4]结合大坝沉降监测的具体实例,应用时间序列分析理论和方法对大坝变形进行预报,该预测方法对短期预报效果更佳,对中长期预报效果不佳;李明然等[5]采用改进的灰色马尔科夫模型进行大坝预测,该研究表明大坝变形监测数据呈现随机性和波动性变化特点,仿真方法的适当与否对大坝变形预测至关重要。
由上述分析可知,由于大坝变形影响参数较多,变化周期不一致,比如,温度变化是日星期型的,水位的变化则以季节为周期,这都极大地影响着大坝变形预测的精度;同时,大部分的预测分析方法或多或少都有着一些缺陷,比如,逐步回归分析模型的精度与观测样本数目有关; 人工神经网络预测方法收敛速度又比较慢等等,这些又影响这大坝变形预测分析的经济性。
为此,本文采用多元线性回归分析方法对大坝变形影响因素进行深入分析,在此基础上引入神经网络模型,构成大坝变形预测混合模型,有效提高了大坝变形预测的精度。
1 大坝变形的影响因素
一般认为,影响大坝变形的3 类因素为: 水压因素H、温度因素T 和时效因素S。其中,水压因素与水库水位密切相关,水库水位与大坝变形之间呈复杂非线性关系,为此,可将水压因素分解成H、H2、H3、H4、H5等5个分量,即大坝变形与水位及水位的2、3、4、5 次方有关; 温度因素又可以分为水温和气温,由于水温变化较小可以省略,而气温变化对大坝的影响又具有滞后效应,为此,选取温度T 和T1 ( 为上一个记录时刻的温度) 作为温度影响因素。再考虑到时效因素,则影响大坝变形参数可分为3 类,共8个变量。
2 大坝变形混合预测模型
2.1 多元线性回归分析简介
多元线性回归分析是将变量一个一个引入,进而通过检验各个变量的偏回归平方和是否显著,以决定是否保留该变量,这样经过显著性判断之后,所保留下来的变量就是对大坝变形影响较显著的变量。
假设随机变量y 与p个自变量x1,x2,…xp之间存在着线性相关关系,实际样本量为n,则其n 次观测值可写为如下形式:

式中: β1,β2,…βp是未知参数; x1,x2,…xp是p个可以精确测量并可控制的一般变量; ε1,ε2,…εn是随机误差。假定εi是相互独立且服从同一正态分布N(0,σ) 的随机变量。
若将方程组(1) 用矩阵表示,则有:

多元线性回归分析的首要任务就是通过寻求β 的估计值b,建立多元线性回归方程见式3,来描述多元线性模型见式1:

2.2 神经网络简介
大坝变形神经网络预测结构,见图1 所示,大坝变形神经网络预测模型由输入层、中间层和输出层组成,其中输入层节点数n 为多元线性分析后保留下的影响参量个数,输出节点只有一个,即大坝变形值。中间层节点数m个,一般m 可取6 ~15个。在模型预测的过程中,将大坝影响参量分别送入输入层的n个节点,而中间层每个节点的输出值为输入层所有节点对其输出的累加( 利用sigmoid 函数计算) ,整个模型的输出,则是中间节点输出与其连接权系数之积的线性和。

图1 大坝变形神经网络预测结构图
2.3 混合模型简介
大坝变形混合预测模型是针对多元线性回归分析和神经网络的缺点构建起来的,即针对大坝实测数据,先使用多元线性回归方法,分析水压等8个因素在大坝变形中的权重,保留影响因素较大的几个参量,舍弃影响因素较小的参量,进而针对保留的参量,引入神经网络模型进行网络训练,最终完成混合预测模型。这样一方面克服了多元线性回归分析在小容量样本下精度不够的问题,又解决了神经网络在变量较多时收敛速度慢,预测解振荡大的特点。
3 实例分析
针对贵州某大坝2002年5月—2007年7月实测数据,共44 组,见表1 以前34 组数据作为大坝变形预测模型的训练样本,以后10 组数据作为预测目标,分别采用多元线性回归分析、神经网络和本文所建立的混合模型进行预测,并比较其精确度。

表1 贵州某大坝实测水平位移及相关数据表
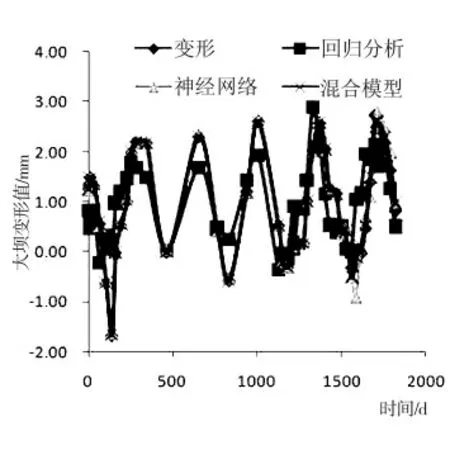
图2 多种预测分析结果比较图
比较图2 可知,多元线性回归分析模型不论是样本训练精度还是预测精度都比较差,只能粗略分析各影响因素之间的权重; 神经网络的样本训练较好,但是预测精度稍差,这与输入影响因素较多,各参量权重不明确有关,而混合模型预测效果最好。

表2 多种预测分析结果比较 mm
表2 表明,采用多元线性回归分析模型的预测结果最大误差为1.5 mm,采用神经网络模型进行预测最大误差为0.71 mm,采用本文提出的混合模型最大误差为0.18 mm,误差最小,预测精度最高,达到了预测目的。
另外,多元线性回归分析结果表明,贵州某大坝变形的关键影响因素为: 水位、水位2 次方、水位3次方、气温和时效性,其中水位和气温的权重最大。
4 结 论
1) 采用多元线性回归分析方法对贵州某大坝进行变形分析,结果表明:水位、水位2 次方、水位3 次方、气温和时效性,其中水位和气温的权重最大。这不仅为大坝变形研究提供了理论依据,也为下一步展开神经网络预测分析奠定了基础。
2) 采用多元线性回归分析和神经网络构建大坝变形预测模型是可行的,实例对比分析结果表明,采用该方法所获得变形预测结果精度最高。
[1]吴中如. 水工建筑物安全监控理论及其应用[M]. 北京:高等教育出版社,2003.
[2]顾冲时,吴中如. 大坝与坝基安全监控理论和方法及其应用[M]. 南京:河海大学出版社,2006.
[3]黄世秀,洪天求,高飞. 基于小波消噪及BP 神经网络的大坝变形分析[J]. 人民长江,2011,42(09) :90 -93.
[4]朱金海,丛枝鲜,李秀海. 大坝变形的动态预报模型研究[J]. 煤炭技术,2009,28(03) ,124 -126.
[5]李明然,田林亚,洪毅. 改进的灰色马尔科夫模型在大坝变形预测中的应用[J]. 水利与建筑工程学报,2012,10(03) :65 -67.
