流域汇流单位线推求方法分析

王丽丽，高志军，田长涛

(1. 孙吴县水文局，黑龙江 孙吴164200;2. 呼玛县水文站，黑龙江 呼玛165100;3. 伊春水文局，黑龙江 伊春153000)

1 流域降雨径流预报方法简介

在水文预报工作中，降雨径流预报方法应用范围较广。应用降雨量预报径流需要解决两个方面的问题:①某次降雨所产生的径流多少。②这些径流是怎样汇集到预报断面的。前者称为产流量预报，后者称为汇流过程预报。从降雨开始到形成流域出口断面流量的整个过程，称为径流的形成过程。这一过程在理论上可分为流域产流和汇流两个阶段:在产流阶段的预报任务就是求出降雨在扣除蒸发、下渗、截留等损失后所产生地表径流的净雨量( 用一次洪水过程的径流深表示) ，一般由流域降雨～径流相关图查得。流域在产流过程中主要受流域内各种因素对降雨的调蓄作用影响，流域的调蓄作用为洪水预报提供了一定的洪峰预见期; 降落在流域上的雨水，从流域各处向流域出口断面汇集的过程称为流域汇流，流域汇流包括坡地汇流和河网汇流两个阶段。实际工作中一般采用净雨量和流域出口断面流量资料，将坡地和河网汇流视为一个总体分析出流域汇流单位线，以用于洪水预报。

2 流域汇流经验单位过程线简介

单位过程线法由L. k. 谢尔曼于1932年提出，至今仍是汇流计算中应用最为普遍的方法。因它是由流域汇流系统实测的雨洪资料反推而得，所以又称为是由黑箱分析法求得的经验单位线。

2.1 单位线的定义

在一个特定的流域上，在单位时段内均匀分布的单位净雨量所形成的流域出口站的地面径流过程线称为单位线。单位线有3个基本要素:①单位线洪峰流量( qm) 。②洪峰滞时( Tp，从净雨中心到单位线洪峰的时距) 。③单位线总历时( TD) 。在我国单位净雨深一般取10 mm，单位时段可根据流域的大小、汇流历时长短和实际需要而定，一般可取1、3、6、12、24 h等，大致是流域出口过程涨洪历时的1/3 ～1/4。

2.2 单位线基本假定

由于实际降雨不可能恰巧是一个单位和上述限定的某段，因此在分析单位线时，要事先作以下基本假定。

1) 在单位时段内净雨深不同，所形成的地面径流过程的总历时相同。

2) 如果单位时段内净雨深不是一个单位，而是n个单位，那么它形成的流域出口流量过程线的流量则为单位线的n 倍。实际进行洪水预报时就是选用适当类型的事先推算出的流域经验单位线，将实际净雨量按与单位净雨的倍比逐时段相乘而得到预报径流过程。

3) 如果净雨历时不是一个时段，而是m个时段，那么各时段净雨量所形成的流量过程之间互不干扰，出口断面的流量等于各时段净雨量所形成的流量之和。

以上3个假定，就是将流域视为线性系统，符合倍比迭加原理。这里着重介绍在汇流分析方面如何选用最佳方法来推求单位线。单位线三要素示意图见图1。

图1 单位线三要素示意图

3 流域汇流单位线推求方法

推求单位线的基本方法是基于上述定义和假定条件。在流域的实测水文资料中选择若干次在洪水量级和降雨时空分布方面有代表性的雨洪过程。各次降雨的历时应较短，洪水过程的峰形要完整，最好是单峰形或易于分割成单峰形的复式峰洪水过程。按事先确定的单位线时段长度Δt 将一次降雨的流域平均降雨过程划分为若干时段，利用本流域已有的产流计算方案来求得各时段的径流量( 净雨量) 。产流方案求出的各时段净雨量总和应与实际选定的洪水过程线径流深一致。由于资料精度、产流方案、洪水过程分割等原因引起两者有一定差异时，应分析原因并做平差修订，一定要使两者相等才能用于推求单位线。

应用已知净雨量及其对应的径流过程推求单位线的方法很多，在系统分析中称为系统识别。在实际工作中应用较多的有直接代数解法、试错法、最小二乘法等，各方法基本原理如下:

已知一次降雨产生的各时段径流深为r1，r2，r3，……，rm，相应的流域出口各时刻流量为Q1，Q2，Q3……，QL。若取单位径流深为10 mm，单位线各时刻纵坐标为q1，q2，q3……，qT。由单位线的基本假定知:直接代数法就是由上述各式解出qi，即:

1) 直接代数解算法计算方便，其明显缺点是误差传递性强，任何时段的Qi或ri有误差时都会依次传递下去而使单位线出现锯齿状甚至负值。再就是在降雨时段较多时( 3 段以上) ，用该方法计算步骤会较多，误差传递现象更加明显。降雨时段越多，降雨与径流之间的假定倍比关系也越加松散，很难得出合理的单位线成果。在实际工作中，能够满足用直接代数法解算单位线的雨洪资料也比较少，因此该方法实际利用率较低。

2) 试错法是先假定一条单位线，根据该假定单位线与已知时段净雨量直接计算流域出流过程，再与实测出流过程进行比较，若两者基本相符，则所假定的单位线即为所求。否则，修正原假定再试算，直至计算值与实测过程相符为止。试错法相当于代数解算法的逆运算，计算步骤简便适合多时段雨洪资料，但计算量较大，试算时间较长且试算时对误差的控制带有主观性，所得的单位线往往不是最优解。

3) 利用最小二乘法推求单位线的基本原理是首先令实测流量为Qo，由单位线推算的流量为Qc，则误差e=Qo－Qc。若取∑e2= min，可将式1 变成方程个数与待求变量相等的正规方程组riqi=Qi，然后解得在最小二乘意义下q 的最优估计值。该方法求解单位线时应用了一次雨洪的全部流量资料，原理上比较完善，但解正规方程组的要求条件较高，不易掌握，而且由于缺少约束条件得到的单位线有时仍会出现锯齿状震荡。

4 利用Excel 线性规划功能推求单位线

本文选择利用Excel 软件中的线性规划功能来推求单位线。线性规划是运筹学中应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。线性规划解决的是线性目标函数在线性约束条件下的最大值或最小值的问题。满足线性约束条件的解叫做可行解，由所有可行解组成的集合叫做可行域。线性规划问题可以表示为:min( z) = cTx ;s. t. Ax = b;x ≥0，上式中，向量x 为可变向量，z 为目标函数，s. t. Ax = b 为线性约束条件( s. t. 意思为“受约束于”) ，A 为系数矩阵。利用Excel 的线性规划功能求解单位线的优点首先在于对使用人员要求起点较低，便于掌握，操作界面简单明了;再就是该法具备试错法和最小二乘法的优点，而且可以灵活设置多项约束条件，可以有效减少和消除解算单位线时易出现的锯齿现象。

4.1 实例应用

选择某水文站的一次洪水过程，断面面积F =552 km2，计算时段△t=3 h，计算结果见表1，并见图6 所示，分析计算过程如下:

4.1.1 数学模型选用

1) min( z) = ∑( Qc－ Qi)2，式中Qc为实测地表径流过程;Qi为计算地表径流过程，目标规划结果为二者误差平方和为最小。

2) s. t. ( Rq) =10;s. t. ( qi) ＞0，式中Rq为单位线径流过程的径流深; 约束条件为解算单位线径流深为10 mm;( qi) 为单位线各时段径流值，约束条件为解算单位线各时段值为非负值。

4.1.2 解算方法

1) 首先在解算表中输入实测地表径流过程和净雨深，再求解单位线一列输入假定的单位线径流过程( 给任意值即可) 。选择“工具”→“加载宏”命令，在弹出的“加载宏”对话框中见图2 确定选中了“规划求解”复选项。

图2 “加载宏”对话框图

2) 见图3 所示设置数据模型计算步骤，在j29 单元格中输入公式=sum( j2; j28) ，此单元格将会作为目标单元格，分析目的是通过改变可变单元格的值使其数值达到最小值。

图3 表格设置与目标单元格确定

3) 选择“工具”→“规划求解”命令，弹出见图4所示的“规划求解参数”对话框。

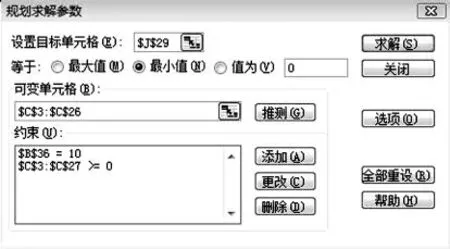
图4 “规划求解”参数设置对话框

在“设置目标单元格”中选择目标函数所在的J29 单元格，在可变单元格中选择可变向量所在的单元格区域C3;C26，可变向量的最终优选结果就是所求的单位线过程。图中“约束”选项用于输入约束条件。本例选择约束条件“$B$36 =10”，目的是使解算的最优单位线径流深为10 mm( 计算公式见表1 备注栏) ;约束条件“$C$3: $C $27 ＞=0”是避免分析出的单位线出现负值。

4) 单击“求解”按钮，Excel 在经过计算之后将得出结果，弹出见图5 所示的“规划求解结果”对话框。最终分析结果见表1。

图5 “规划求解”结果对话框

通过表1 和图6 可见，利用解算单位线推求出的地表径流过程与实测地表径流过程基本一致，单位线径流深控制为10 mm。洪峰流量计算误差为2.7%，满足水文预报规范要求的计算误差须小于实测洪峰流量值20%的精度标准。

图6 线性规划法求得单位线、实侧和计算径流过程图

表1 利用Excel 规划求解功能分析解算单位线实例计算表

5 结 语

1) 利用线性规划方法推求单位线基于线性数学模型和误差控制以及相应约束条件为基础。该方法使用要求较低，在推求单位线时，Excel 软件能够自动对单位线各时段流量进行优选确定，避免了其它方法分析单位线费时费力的弊端。线性规划法分析单位线时对约束条件的设置可以在最大程度上减少单位线某一时段出现负值和线形呈现锯齿现象。

2) 对单位线成果的检验要以实用性为原则，不应仅以满足单位线径流深接近10 mm为标准。由于实际洪水预报主要以预报洪峰流量为主，因此利用单位线计算出的峰值必须与实测洪水峰值一致或接近，否则应对单位线峰值进行必要的修正。

3) 由于任何实测雨洪资料都可能存在不同程度的观测误差和特殊成因，因此有些入选的雨洪资料在采用本文所述方法时系统会出现无法提供最优解的情况，此时应对雨洪关系和数值进行重新审核、取舍和确认，在以提高洪峰流量拟合精度为主要目标的前提下对单位线其余部分进行必要的修正处理。

［1］邓先俊. 陆地水文学［M］. 北京:水利电力出版社，1984.

［2］李慧珑. 水文预报［M］. 北京:水利电力出版社，1979.

［3］宋少忠.Excel 公式、函数和图表应用与实例分析［M］.北京:中国水利水电出版社，2008.