数学建模中的方程思想及其应用*

洪宝剑

(1.南京工程学院;2.江苏大学)

0 引言

伴随着现代社会的高速发展，数学知识的应用已经深入到众多的自然科学和社会科学领域.除了研究数学的专业人才之外，社会还需要大量会用数学知识来解决实际问题，去创造效益的人才，这个过程就是通常所说的数学建模.数学模型［1］是根据现实世界某一现象特有的内在规律，做出一些必要的简化假设，运用适当的数学工具，得到的一种抽象简化的数学结构.这些结构可以是方程、公式，算法、表格、图示等等.而数学建模就是运用数学的语言和方法建立数学模型.如何在大学数学教学中渗透数学建模思想，对于培养学生学习数学的兴趣，提高学生的思维创新能力有重要作用.

数学建模是利用数学工具解决实际问题的动态过程，这就特别体现了“用数学”的思想.建立数学模型的方法有很多，比如运用概率论方法建立随机模型［2］;运用微元法思想建立积分模型［3］;运用图论思想建立网络模型［4］等等.本文重点研究应用方程思想建立数学模型.

对于现实世界的变化，人们关注的往往是其变化速度以及所处位置随时间的连续发展规律，其规律一般可以用微分方程(组)来表示，在现实社会中，又有许多变量是离散变化的，如人口数、生产周期与商品价格等，这时其规律就要用差分方程(组)表示，因此实际问题只要涉及“改变，变化，增加，减少，衰变”等等词语的，都可尝试用方程建立模型.如:投资、还贷、减肥、养老金、种群增长、疾病传播、化学反应、污染控制、空间飞行、军事战斗等等实际问题，对这些动态过程建立数学模型，能够表现这些过程的演变，并给出分析和预测.其中的连续模型适用于常微分方程和偏微分方程建模，离散模型适用于差分方程建模.下面以几个例子做说明.

1 应用举例

1.1 常微分方程建模

主要用于处理那些描述动态过程的状态变量随时间连续变化的实际问题.

例1 人口增长的逻辑斯蒂(Logistic)方程模型(一阶常微分方程模型)18世纪末，英国人马尔萨斯(Malthus)在研究了百余年的人口统计资料后认为，在人口自然增长的过程中，净相对增长率(净增长率比上总人数)是常数.出生率减去死亡率为净增长率.在此假设下，推导出人口随时间变化的数学模型，分析该模型的优缺点，并进行改进.

解:据假设，在t到t+Δt时间段内，人口的增长量为 N(t+Δt)-N(t)=rN(t)Δt，并设 t0时刻的人口数为N(t0)，于是

用分离变量法易求出其解为:N(t)=N0er(t-t0)，这里r，N0可以通过统计历史数据得到.此式表明人口以指数规律随时间无限增长.这个公式非常准确地反映了在1700-1961年间世界人口总数.但是，按此模型计算，到2670年，地球上将有36000亿人口.这是非常荒谬的.因此，这一模型应该修改.考虑到地球上的所有资源只能供应一定数量的人生活，1838年荷兰生物数学家韦尔侯斯特(Verhulst)引入常数Nm，用来表示自然环境条件所能容许的最大人口数，并且假设净增长率等于r(1-N(t)/Nm)，由韦尔侯斯特假定，马尔萨斯模型应改为

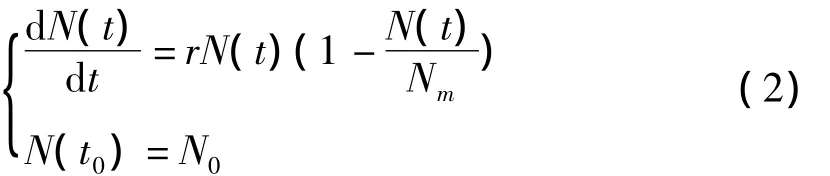
例2 导弹追踪问题(二阶常微分方程模型)

设敌舰在我舰正东方向d km处，行驶速度为v0km/min，行驶方向与正东方向的夹角为θ，导弹的飞行速度为v km/min.现根据情报，这种敌舰能在我舰发射导弹后T min做出反应并摧毁导弹.试问，如何改进电子导弹系统，使其根据敌舰与我舰的距离，行使方向和速度，能自动判断出敌舰是否在有效打击范围之内.

解 问题的关键是计算出导弹击中敌舰所需要的时间t*，并将t*与T比较，若t*＜T，则敌舰在打击范围内.我们仍以我舰位置为坐标原点，以正北方向为y轴建立坐标系，设t时刻导弹所处的位置为P(x(t)，y(t))，敌舰所处位置为 Q(d+v0tcosθ，v0tsinθ).如图2 所示.

图1 Logistic曲线

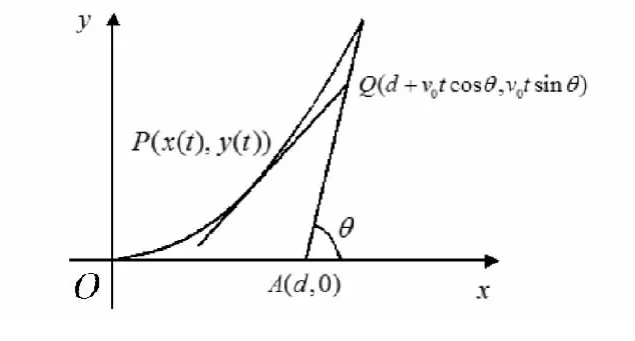
图2 导弹追踪问题

由于导弹头始终对准敌舰，因此直线PQ是导弹运行轨迹OP在P点的切线，即

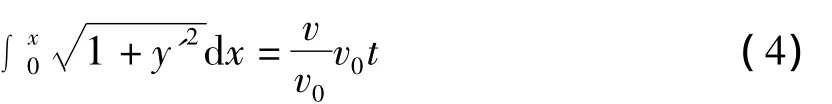
联立方程(3)和(4)，消去t，再对方程两边对x求导，得到二阶常微分方程

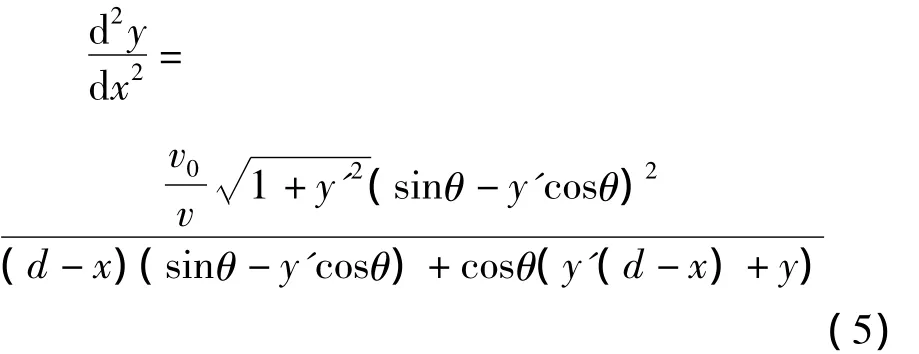
当P和Q两点的运动曲线相遇时，导弹击中敌舰.因此，若x*、y*满足方程(5)且

则点(x*，y*)为导弹击中敌舰的击中点.再根据Q 点的表达式 Q(d+v0tcosθ，v0tsinθ)，可以计算出击中时间若 t*＜T，则敌舰在打击范围内，可以发射.

在现实生活中各式各样的追击问题，如狼追兔子，狮子捕杀鹿，导弹追踪敌机等等追击模型都可以归结为二阶微分方程模型.

1.2 差分方程建模

如果描述动态过程的状态变量在离散时段上发生变化，这时就要考虑用差分方程建模.

例3 离散的人口增长模型.

假设人口的增长主要归结为生育，以某一离散时段(如25岁)为周期进行生育.

解 不妨用yk表示第k代的人口数量，则得到下列模型

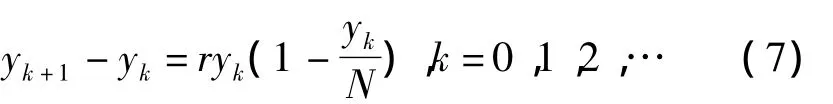
即为

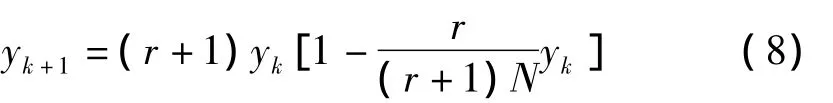
其中r为固有增长率，N为最大容量.

若 yk=N，则 yk+1，yk+2，… =N，y*=N 是平衡点.

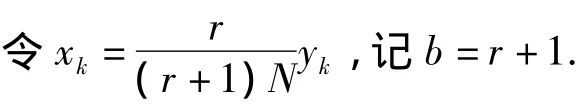
式(8)化为

这是一阶非线性差分方程，无须求出xk，事实上，只要给出x0，利用数学软件就可以递推出xk.仅考虑平衡点:x=f(x)=bx(1-x)，则，因为f'(x*)=b(1-2x*)=2-b，当|f'(x*)|＜1时稳定，当|f'(x*)|＞1时不稳定.所以，当1＜b＜2或2＜b＜3时.当 b＞3时，xk不稳定.如图3-图5所示.

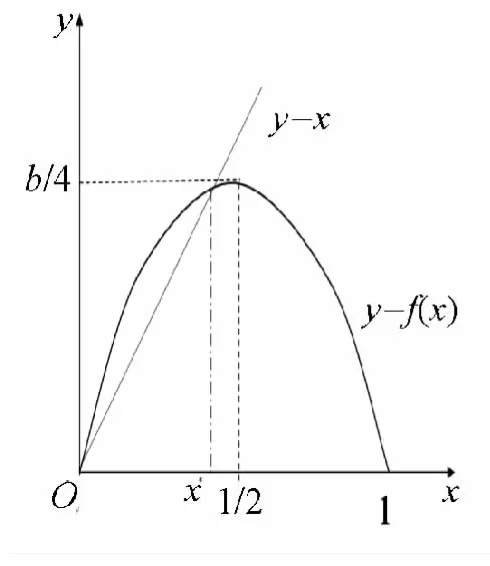
图3 1＜b＜2

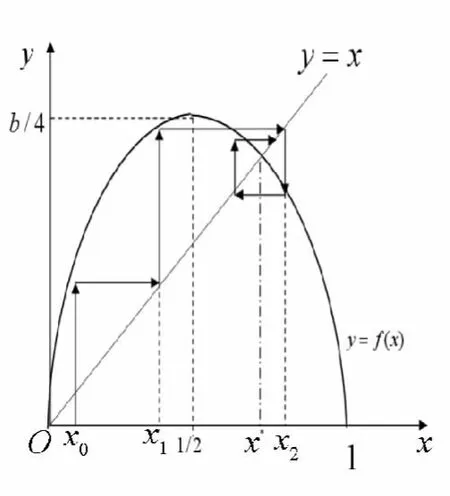
图4 2＜b＜3

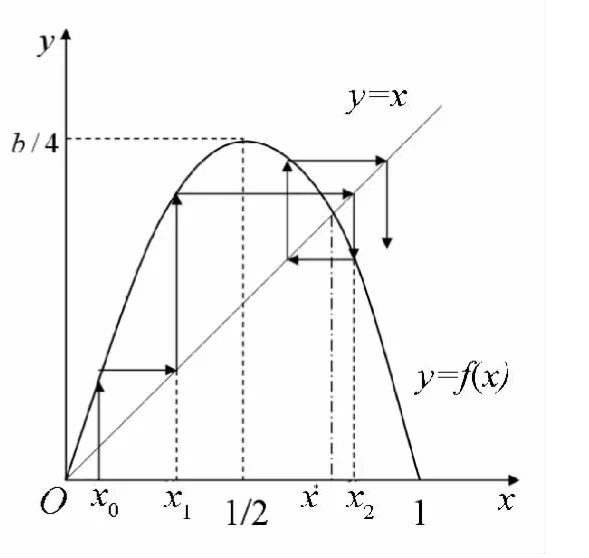
图5 b＞3

此外，以一定周期变化的实际问题都可以考虑采用差分方程建模，如:市场经济中的蛛网模型，减肥计划模型，养老保险模型，种群增长模型等等.

1.3 偏微分方程建模

在处理描述动态过程的状态变量随时间连续变化的实际问题时，如果考虑的自变量的个数为两个或两个以上，这时就要考虑用偏微分方程建模.

例4 人口增长模型的再次修正.

Verhulst模型改进了马尔萨斯的一些弊端，但它和马尔萨斯模型都将生物群体中的每一个个体视为同等地位来对待的，这个原则只适用于低等动物，对于人类群体来说，必须考虑不同个体之间的差别，特别是年龄因素的影响.不考虑年龄因素就不能正确地把握人口的发展动态.

解 人口的数量，出生率、死亡率等量不仅和时间有关，还应该和年龄有关，这时，得到用偏微分方程描述的人口模型:

其中，p(t，r)表示任意时刻t按年龄r的人口分布密度，μ(t，r)表示年龄为 r的人口死亡率，φ(t，r)表示年龄为 r的人口迁移率，β(r，t)表示年龄为r的人的生育率(可进一步细化为β(r，t)=b(t)k(r，t)h(r，t)，b(t)为总和生育率，k(r，t)为女性比例，h(r，t)为生育模式.)r1表示可以生育的最低年龄，r2表示最大年龄，该模型中的人口分布密度、死亡率和出生率均与年龄有关，这与现实情况相符，因此，这个模型确实更能精确地描述人口的发展过程.

如果上述方程把年龄视为恒定，则退化为常微分方程，若令 μ(t，r)=-r，p(t，r)=N(t)，N(0)=N0，φ =rN2(t)/Nm即变为 Verhulst模型.

此外物理中的半导体模型［5］、生态学中的传染病模型［6］等等，都可以用偏微分方程建立.

2 结束语

在数学教学中融入数学建模思想［7-8］，在数学建模的过程中充分应用方程的思想和理论，不仅可以激发学生学习大学数学的兴趣，使学生了解数学知识在实际生活中的应用，还能提高学生运用数学知识解决实际问题的能力，为后续课程的学习打下坚实的基础，真正做到“学以致用”.这对大学数学的教学改革和课程建设都将起到积极的推动作用.最后，与其说数学建模是一门技术，不如说是一门艺术，它需要熟练地数学技巧，丰富的想象力和敏锐的洞察力，需要大量阅读，思考别人做的模型，尤其要自己动手，亲身体验.熟练掌握方程思想及理论对于提高数学建模水平有着重要意义.

［1］ 姜启源，谢金星，叶俊.数学模型:第三版［M］.北京:高等教育出版社，2003.

［2］ 陈华，奚敏.概率模型构造及其思维方法［J］.青岛理工大学学报，2006，27(5):124-126.

［3］ 王庚，张珠宝.数学建模融入微积分教学单元［J］.大学数学，2006，22(4):31-35.

［4］ 张彦超，刘云，张海峰，等.基于在线社交网络的信息传播模型［J］.物理学报，2011，60(5):050501-050506.

［5］ 叶其孝，李正元.反应扩散方程引论［M］.北京:科学出版社，1999.

［6］ 马知恩，周一仓，王稳地，等.传染病动力学的数学建模与研究［M］.北京:科学出版社，2004.

［7］ 阮妮.融入数学建模思想的常微分方程教学初探［J］.大学教育，2013(8):67-68.

［8］ 王晓.在偏微分方程教学中融入数学建模思想［J］.怀化学院学报，2009，28(11):112-113.