三维单李代数sl(2,F)上的Yang-Baxter方程
2013-10-24高岩
高 岩
(哈尔滨师范大学)
0 引言
Baxter代数由Baxter于1960年提出,源于Glen Baxter概率论中波动理论积分方程[1].Rota在90年代对Baxter算子进行了更深入的研究.[2]近年来,Baxter代数在理论物理和数学物理方面得到了广泛而显著的应用,许多学者刻画了低维代数上的Rota-Baxter算子.例如,文献[3]给出了维数小于等于3时权0的结合代数上的Rota-Baxter算子,文献[4]给出了维数小于等于3时权1的Rota-Baxter算子,而文献[5]对权0的二阶矩阵构成的四维结合代数上的Rota-Baxter算子进行了研究.代数闭域F上权0的Rota-Baxter算子称为Yang-Baxter方程.该文刻画了三维单李代数sl(2,F)上的Yang-Baxter方程.
1 基本概念
该文规定F为特征p≠2的代数闭域,L是域F上的李代数,用[,]表示李乘.
定义1[6]设L是域F上的一个李代数,若R是L×L→L的线性算子,满足
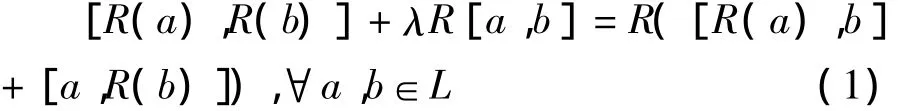
则称R是一个权为λ的Rota-Baxter算子,L是一个权为λ的Rota-Baxter代数,当λ=0时称上式为Yang-Baxter方程.
令{e1,…,en}是李代数L的一组固定基,设,其中∈F.L上的任意Rota-Baxter算子R都可以写成矩阵(rij)形式,其中rij由唯一确定,易见rij满足如下方程(λ=0):
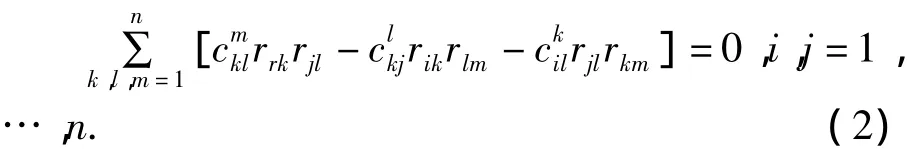
2 Yang-Baxter方程
记L=sl(2,F)是域F上的一个三维单李代数,其中L的标准基为:
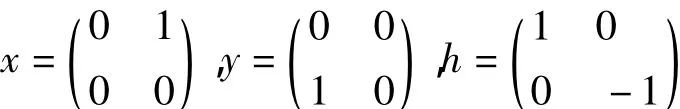
规定基元素间的乘法表:[x,y]=h,[h,x]=2x,[h,y]=-2y.
命题1 三维单李代数L上Yang-Baxter方程的解共有9个(任何参数属于代数闭域F,且 a,b≠0):

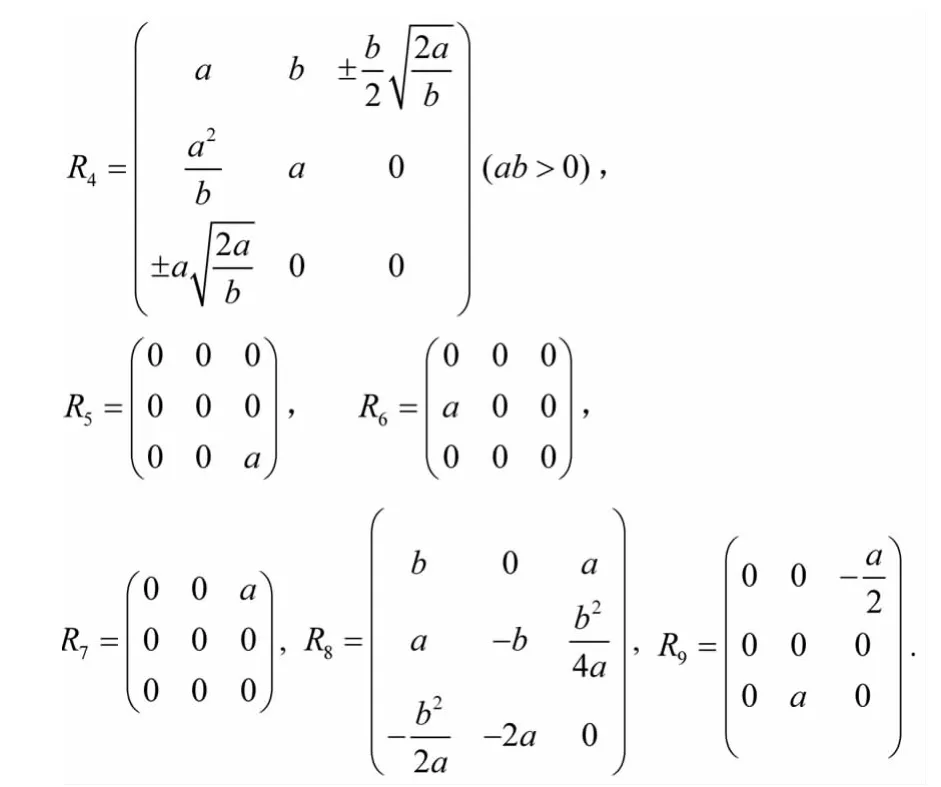
证明 由定义可知三维单李代数L上Yang-Baxter方程的解即为权0时的Rota-Baxter算子.
根据L的标准基,则L上任意Rota-Baxter算子R能够由矩阵(rij)表示,
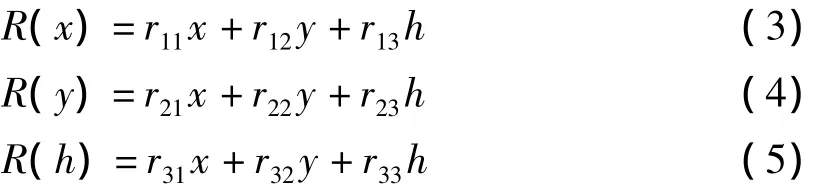
且 R(x),R(y),R(h)满足(1)式,由 L的基的乘法表可以得到以下9个等式:
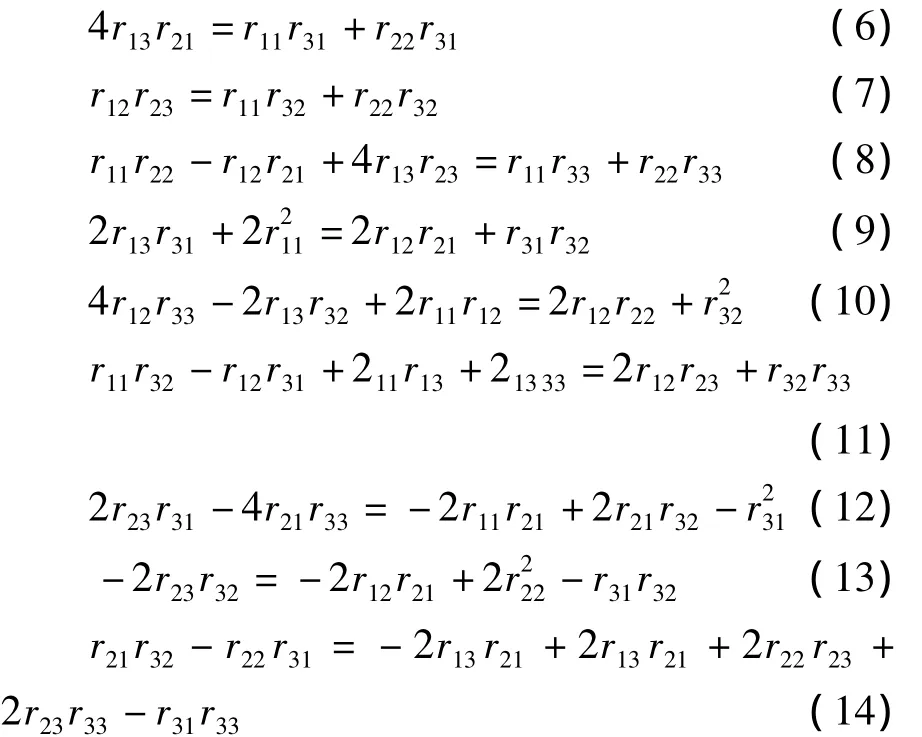
则上述命题的证明能够分成以下六种情况:

则在以下的六个引理中分别考虑这些情况.
引理1 当r32=0,r12=0,r23≠0时,L上的Yang-Baxter方程的解由上述命题中的R1与R2给出.
证明 由(13)推出r22=0,由(11)对r13=0进行分类讨论:(i)当r13=0时,通过计算可得命题1中的R1和R2.(ii)当r13≠0时,通过计算可知此情况下Yang-Baxter方程无解.
引理2 当 r32=0,,r12=0,r23=0时,L上的Yang-Baxter方程的解由上述命题中的R3与R4给出.
证明 由(13)推出r12r21=代入(8)有r22(r11-r22)=r11r33+r22r33(*),由(13)且 r12≠0推出2r33+r11=r22推出r11-r22=-2r33代入(*)推出-2r33r22=(r11+r22)r33,则下对r33进行分类讨论:(i)当r33≠0时,通过计算可知此情况下Yang-Baxter方程无解.(ii)当r33=0时,可得命题1中的R3和R4.
引理3 当 r32=0,,r12=0,r23=0时,L上的Yang-Baxter方程的解由上述命题中的R5与R7给出.
证明 由(13)推出r22=0,由(8)推出r11r33=0,下分类讨论:(i)当r11=0,r33≠0时,计算可得命题1中的R5.(ii)当r11≠0,r33=0,时,由(11)推出r13=0,由(9)推出 r11=0,与 r11≠0矛盾,故此种情形不存在.(iii)当r11=r33=0时,可得命题1中的R6与R7.
引理4 当r32≠0,r12=0,r23≠0时,L上的Yang-Baxter方程的解由上述命题中的R8给出.
证明 由(10)推出r32=-2r13,令r13=a≠0,推出r32=-2a≠0,由(11)推出 r33=0,由(7)推出r11=-r22=b≠0,代入(6)推出r21=0,由(8)推出,由(9)推出r=31,则可得命题1中R8.
引理5 当r32≠0,r12≠0,r23≠0时,L上的Yang-Baxter方程无解.
证明 由(7)推出r11=-r22=a≠0,由(8)推出r12r21=-a2,推出,由(8)推出r13=0,又由于 r32≠0,故令 r32=1,则由(9)推出,由(10)推出,但这些未知元的值不满足方程(12)和(14),故此时L上的Yang-Baxter方程无解.
引理6 当r32≠0,r12=0,r23=0时,L上的Yang-Baxter方程的解由上述命题中的R9给出.
证明 由(10)推出 r32=-2r13=a≠0,推出,由(7)推出r=-r,由(8)1122推出r11r22=0推出 r11=r22=0,由(11)推出r33=0,由(13)推出 r31=0,由(6)推出 r21=0,由(12)推出r31=0,则可得命题1中的R9.
[1] Baxter G.An analytic problem whose solution follows from a simple algebraic identity[J].Pacific J Math,1960,10:731-742.
[2] Rota G C.Baxter algebras and combinatorial I[J].Bull AMS,1969,5:325-329.
[3] Li X X,Hou D P,Bai C M.Rota-Baxter operators on pre-Lie algebras[J].J Nonlinear Math Phys,2007,14:269-289.
[4] Huihui A,Bai C M.From Rota-Baxter algebras to pre-Lie algebras[J].J Phys A:Math Theor,2008,41:015201-015219.
[5] 孙琼.一类Baxter代数及其应用.黑龙江大学硕士论文,2012:4-11.
[6] 苏育才,卢才辉,崔一敏.有限维半单李代数简明教程.北京:科学出版社,2008.
