基于灰色系统理论的我国R&D人力投入预测*
2013-10-24詹厚龙
黄 飞, 詹厚龙
(重庆工商大学 数学与统计学院,重庆 400067)
基于灰色系统理论的我国R&D人力投入预测*
黄 飞, 詹厚龙
(重庆工商大学 数学与统计学院,重庆 400067)
采用灰色预测模型对我国2001-2011年的R&D人员全时当量年度数据进行拟合和预测。研究表明:GM(1,1)模型较好的拟合和预测了我国R&D人员全时当量及其配置结构,未来一段时间(2012-2015年)我国R&D人力投入将会逐步加大,但R&D人力投入的配置结构将更加失衡。因此,未来我国R&D人力投入在加大力度的同时,更需要合理科学的配置。
灰色系统理论;R&D人员全时当量;基础研究;应用研究;试验发展
R&D活动,即科学研究与试验发展活动,是指为了增强知识的总量,包括有关人类、文化和社会方面的知识,以及运用这些知识去创造新的应用而进行的系统的、创造性的工作[1]。R&D活动是科技创新的核心,而R&D活动的主体是R&D人员。在未来的国际竞争中,R&D人力投入是科技竞争力的决定因素。因此,预测我国未来R&D人力投入对我国未来科技创新发展具有重要意义。国际上通用的比较科技人力投入的指标是R&D人员全时当量,它指R&D全时人员(全年从事R&D活动累积工作时间占全部工作时间的90%及以上人员)工作量与非全时人员按实际工作时间折算的工作量之和[2]。基于此将采用灰色系统理论预测我国未来的R&D人员全时当量及其在基础研究、应用研究、试验发展各阶段的配置情况,以期为我国科技人力投入提供实证依据。
1 灰色预测建模原理
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,即是对一定范围内变化的、与时间有关的灰色过程的预测[3]。我国R&D人员全时当量随着年份的增长而不断增加,可以用灰色预测模型对我国R&D人员全时当量做较全面的分析,并做短期的预测。灰色系统理论建模的主要任务是根据具体灰色系统的行为特征数据,充分开发并利用不多的数据中的显信息和隐信息,寻找因素间或因素本身的数学关系。通常的办法是采用离散模型,建立一个按时间做逐段分析的模型。
灰色系统常用的预测模型是GM(1,1)模型,GM(1,1)模型表示一阶的、单变量的线性动态预测模型,其预测原理是将离散的随机数,累加各列变成随机性被显著削弱的较有规律的生成数,在此基础上建立数学模型,建模步骤如下:
1.1 生成时间序列
设研究对象的历史数据为:X(0)=(X(0)(1),X(0)(2),…,X(0)(n)),由于原始数据的随机性和无规律性,需要对原始序列进行数据处理,通过累加生成方式将原始序列转换为规律性较强的递增数列:X(1)=(X(1)(1),X(1)(2),…,X(1)(n))。其中,累加生成列公式:

1.2 灰色预测模型GM(1,1)的建立
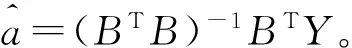
1.3 灰色预测模型的检验
灰色预测检验一般分为残差检验、关联度检验和后验差检验。
1.3.1 残差检验
对模型预测还原值与实际值的残差进行逐点检验,通过计算绝对误差和相对误差,检验判断误差变动是否平稳。

相对残差序列φi=Δ(0)(i)/X(0)(i)。
1.3.2 关联度检验
关联度检验是通过考察模型值曲线与建模序列曲线的相似程度进行检验。关联度说明两个序列之间的关联程度,用来描述模型模拟值序列对原始序列值拟合的程度,根据经验,当λ=0.5时,关联度大于0.9、0.8、0.7、0.6所对应的模型分别为优、合格、勉强合格、满意。
1.3.3 后验差检验
对残差分布的统计特征进行检验。


(3) 计算方差比:C=S2/S1

一般根据下表检验模型的拟合精度,精度等级分为4种:优、合格、勉强合格、不合格。

表1 模型精度等级表
2 实证分析
R&D人员全时当量主要分为基础应用研究人员全时当量、应用研究人员全时当量、试验发展人员全时当量。采用《2012年中国科技统计年鉴》中2001-2011年R&D人员全时当量及其在基础研究、应用研究、试验发展三个阶段的年度数据,应用灰色系统理论,分别建立GM(1,1)模型,对我国R&D人员全时当量及其配置结构进行拟合和预测。
2.1 建立GM(1,1)模型
根据上述灰色预测模型GM(1,1)的原理,通过Matlab软件编程计算得到的我国R&D人员全时当量、基础研究全时当量、应用研究全时当量、试验发展全时当量的灰色预测模型如下:
R&D人员全时当量总量:
X(1)(k+1)=715.255 5e0.123 7k-619.605
(1)
基础研究人员全时当量:
X(1)(k+1)=97.417 8e0.087 2k-89.537 8
(2)
应用研究人员全时当量:
X(1)(k+1)=746.701 8e0.133 4k-724.102
(3)
试验发展人员全时当量:
X(1)(k+1)=388.635 2e0.147 9k-323.465
(4)
2.2 GM(1,1)模型的检验
根据上述预测模型计算我国R&D人员全时当量、基础应用、应用研究、实验发展各序列的残差、关联度、后验差,参数如表2。
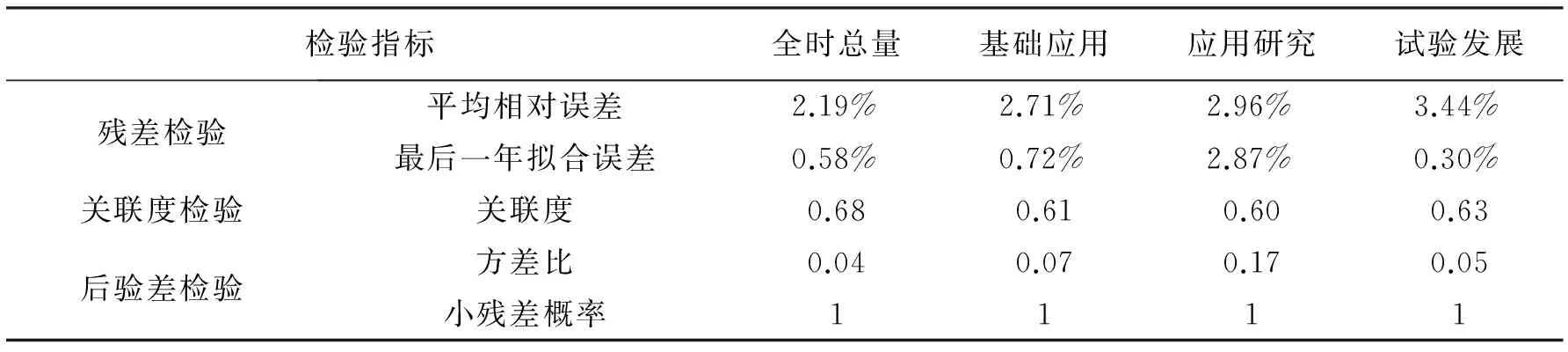
表2 灰色模型检验指标
表2为我国R&D人员全时当量、基础研究人员全时当量、应用研究人员全时当量、试验发展人员全时当量灰色模型预测的各项指标检验结果。
从残差检验检验的结果看,各项人员全时当量的检验结果均小于检验水平5%,且最后一年拟合误差均在5%以下,认为模型在5%的检验水平下时平稳的,即认为模型合格;从关联度检验的结果看,各项人员全时当量的关联度均大于0.6,可见,预测模型拟合程度较好,这一点可以从图1中看出来;从后验差检验的结果看,方差比均在0.35以下,认为模型优;小残差概率均为1,大于检验标准0.95,认为模型优。进一步检验模型的精度等级,通过表1中的标准可以看出,各项人员当量的方差比和小残差概率均满足1级标准。因此认为模型精度优。
综上分析,我国R&D人员全时当量、基础研究人员全时当量、应用研究人员全时当量、试验发展人员全时当量均通过残差检验、关联度检验、后验差检验,且模型满足1级精度标准。
2.3 灰色预测模型拟合
GM(1,1)模型的检验结果显示灰色预测模型满足1级精度标准,则可采用GM(1,1)进行预测,2001-2011年R&D人员全时当量、基础研究全时当量、应用研究全时当量、试验发展研究当量的拟合情况如图1。
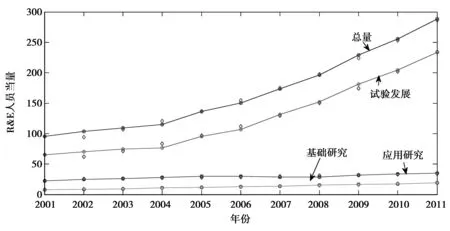
图1 2011-2011年R&D人员全时当量GM(1,1)预测
从图1中可以看出灰色拟合预测情况的特点,即:我国R&D人员全时当量、试验发展人员全时当量、应用研究人员全时当量、基础研究人员全时当量的各年的预测点紧紧围绕着实际点上下波动,其波动幅度很小;试验发展人员全时当量的投入曲线与R&D人员全时当量投入的曲线增长幅度基本一致,上升趋势很明显,特别是2004年之后;应用研究人员全时当量、基础研究人员全时当量的增长趋势平稳,增长幅度较小。
2.4 我国R&D人员全时当量预测
基于2001-2011年的历史数据所建立的灰色预测模型,分别预测2012-2015年我国R&D人员全时当量、基础研究人员当量、应用研究人员当量和试验发展人员当量,结果如表3。

表3 2012-2015年R&D人员全时当量预测值 万人/年
从2012-2015年R&D人员全时当量的预测值来看,2012-2015年我国R&D人员全时当量预测值具有以下特点:
(1) R&D人员全时当量总量显著增加。具体表现为:我国R&D人员全时当量在2015年将达到470.04万人/年,其中基础研究人员全时当量、应用研究人员全时当量和实验发展人员全时当量分别为27.59万人/年、37.88万人/年、423.55万人/年。
(2) 基础研究、应用研究、试验发展人员全时当量年平均增速有明显差异。具体表现为:R&D人员全时当量总量在2012-2015年平均增长速为13.6%,但其各研究阶段R&D人员当量年平均增速有明显差异,试验发展人员全时当量平均增长速度最高为15.94%,基础研究人员全时当量和应用研究人员全时当量的平均分别为9.13%、3.34%,明显低于总体平均增长速度。
2012-2015年我国R&D人员全时当量的配置结构预测图(图2)则更具体的揭示了R&D人员全时当量在2012-2015年配置结构情况。

图2 2012-2015年我国R&D人员全时当量配置结构预测
由图2可知,2012-2015年我国R&D人员全时当量预测的配置结构基本特征为:
(1) 基础研究比例最低,应用研究第二,且两者均逐年降低。至2015年,基础研究R&D人员全时当量占比仅为6.40%,应用研究仅为8.79%。
(2) 试验发展R&D人员全时当量占我国R&D人员全时当量的绝大部分。至2015年,试验发展R&D人员全时当量占比将达到84.80%。
3 结论及建议
基于灰色系统理论对2001-2011年我国R&D人员全时当量总量及其在基础研究、应用研究、试验发展全时当量的年度数据进行灰色拟合,残差检验、关联检验、后验差检验结果显示,各灰色预测模型均满足1级精度标准。根据已经过检验的灰色预测模型,预测2012-2015年我国R&D人员全时当量总量及其在研究阶段间的配置结构,预测结果显示:2012-2015年间R&D人员全时当量总量将按照年均13.16%的增速发展,即R&D人员投入的力度在未来4年将继续加大;2012-2015年R&D人员全时当量在研发阶段(基础研究、应用研究、试验发展)上的配置将更失衡,试验发展研究比例继续扩大,同时基础研究、应用研究比例逐年降低。可见,未来我国R&D人力投入不仅要继续加大力度,更要注意R&D人力投入在基础研究、试验发展、应用研究间的配置,合理科学地安排R&D人力投入。
[1] 袁卫.中国R&D理论、方法及应用研究[M].北京:中国人民大学出版社,2009
[2] 吴林海,杜文献,童霞.中国未来R&D投入配置的理论与实证研究[M].北京:化学工业出版社,2009
[3] 杨德平.经济预测方法及MATLAB实现[M].北京:机械工业出版社,2012
[4] 李恩平.山西省综合配套试验改革背景下科技人才需求预测研究[J].科技和产业,2012(3):51-58
[5] 朱昌明.基于灰色预测的湖北省R&D资源发展的趋势分析[J].科技创业月刊,2012(8):14-17
[6] 詹锦华.中国城镇居民收入和消费的灰色预测.[J].重庆工商大学学报:社会科学版,2009(2):42- 46
Human Input Prediction for China’s R&D Based on Grey System Theory
HUANGFei,ZHANHou-long
(School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)
This paper uses grey prediction model to conduct fitting and prediction for the annual data of R&D personnel FTE of China during 2001-2011, and the research shows that GM(1,1) model better fits for and predicts China’s R&D personnel FTE and its matched structure, that China’s R&D personnel input will be enlarged in the future (2012-2015), however, the matched structure for R&D personnel input will be more unbalanced. Thus, in the future, scientific and reasonable allocation of China’s R&D personnel is more needed while China’s R&D personnel input is enhanced.
grey system theory;R&D personnel FTE;basic research;applied research;experiment development
1672-058X(2013)09-0051-05
2013-04-17;
2013-04-24.
重庆工商大学创新型项目(yjscxx2012-037-36, yjscxx2012-037-37, yjscxx2013-026-09).
黄飞(1988-),女,重庆石柱人,硕士研究生,从事社会经济统计学研究.
F202
A
责任编辑:李翠薇
校对田静
