基于FEM－SPH 耦合方法的AISI4340钢超精密切削过程仿真

郭晓光，魏延军，张小冀，金洙吉，郭东明

（大连理工大学 精密与特种加工教育部重点实验室，辽宁 大连 116024）

0 引言

超精密切削是20世纪60年代发展起来的新技术，它在国防和尖端技术的发展中起着重要作用.目前采用得到广泛应用的单点金刚石切削技术（SPDT），可以获得纳米级表面粗糙度［1］.超精密切削服从金属切削的普遍规律，同时也有不少特殊规律.

切削实验是研究超精密切削机理的重要途径，但它需要精密的实验及检测设备且费时费力.20世纪70年代，人们开始将有限元方法应用于切削过程的研究［2］.有限元方法的一个显著优点在于它可以清晰地描述切削过程中的瞬态应力、应变等，从而为材料去除机理的研究提供有效途径.近年来，有限元模型逐渐由二维平面应变模型发展为三维模型［3］.

但是传统的有限元方法依赖于有限元网格，在处理大变形问题时网格畸变往往导致计算崩溃.而且有限元方法需要人为设定分离准则，与实际情况相差较大，这些都限制了有限元法在切削过程仿真中的应用.近年来发展起来的无网格法为切削模拟提供了新的途径，光滑粒子动力学（smoothed particle hydrodynamics，SPH）法是其中发展较为成熟的方法.SPH 法由Lucy 等提出［4－5］，最早应用于天文学领域.由于不依赖于网格，而是采用粒子划分，可以避免网格畸变，准确反映大变形问题中材料的本构行为［6］.

传统有限元方法作为一种发展成熟的数值方法，与无网格方法相比，具有更高的计算效率和便捷的边界处理方法.无网格法计算效率较低，但模拟切削时具有两个主要优势：（1）可以避免网格畸变问题，更好地模拟切削层材料的大变形；（2）无需人为设置材料的分离准则，能够更加自然地模拟切屑的形成过程［7］.近年来研究者开始将SPH法应用到切削过程的模拟中.Heinstein等［8］证明了SPH 法在直角切削模拟中的有效应用.Limido等［9］采用SPH 法对高速切削过程进行模拟，分析了切屑的形成并进行了切削力预报.王永刚［10］采用SPH 法研究了超精密切削切屑的形成机理.Bagci［11］采用SPH 法对切削过程中材料内部应力、应变进行了分析.

但以往研究多针对应力场的计算而未考虑温度的变化，而实际切削会产生大量的热，是热力相互作用的过程.本文结合有限元法与SPH 法各自的优点，建立AISI4340钢金刚石超精密切削过程的FEM－SPH 耦合模型，同时将热分析考虑在内，采用LSTC 公司开发的大型商用动力学分析软件LS－DYNA 进行模拟计算，研究AISI4340钢超精密切削机理.

1 SPH 法的基本原理

与有限元法不同，SPH 法的离散化使用固定质量的可动点而非网格.从计算的角度来看，SPH法是把物理流场用有一定流动速度的运动质点集来描述，每个质点就是已知流场特性的插值点，整个问题的解通过这些质点的规则插值函数来得到，守恒方程用通量或质点内力来等效表示.

SPH 法的基础是插值理论.任一宏观变量如密度、压力、温度等可以方便地借助于一组无序点上的值表示成积分差值计算得到.各质点的相互作用借助于插值函数来描述.利用插值函数给出量场在一点处的核心估计值，将连续介质动力学的守恒定律由微分方程形式转换成积分形式，进而转换为求和.图1形象地表示了有限元近似与SPH 近似的区别，可以看出，后者比前者要“光滑”得多.

图1 有限元法与SPH 法的比较［12］Fig.1 Comparison between FEM and SPH method［12］

SPH 法中质点近似函数定义为

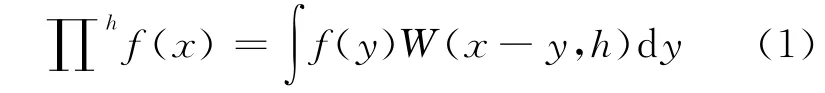
其中核函数W使用辅助函数θ进行定义：

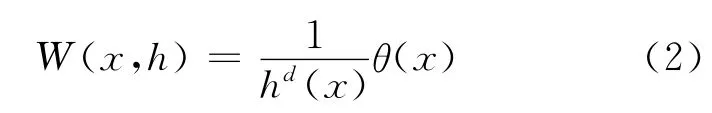
式中：d为空间维数，h为光滑长度.辅助函数可由下式表示：

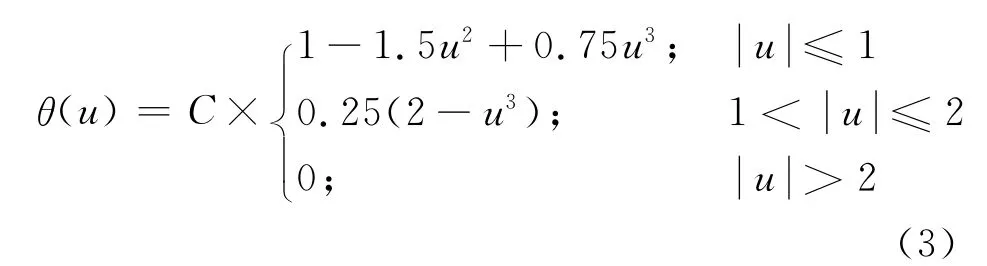
式中：C为归一化常量，由空间维数确定［7］.

2 仿真模型的建立

2.1 FEM－SPH 耦合模型

采用有限元软件ANSYS12.0建立切削模型有限元部分.由于ANSYS 不支持建立SPH 粒子，SPH 部分使用LSTC 公司专门开发的软件LS－PREPOST 建立.

AISI4340钢超精密切削的FEM－SPH 耦合模型如图2所示.为减少计算量，本文简化了计算模型，工件设置成20μm×10μm×2μm 大小的长方体.其中切削变形区划分为120 000个SPH 质点，其他部分及刀具采用有限元网格进行划分.SPH质点可以自由运动，质点之间不存在拓扑关系，从而可以在刀具的作用下实现切屑的自然分离［13］.

刀具沿X轴负方向作直线运动，因此对其Y、Z方向自由度及全部转动自由度进行约束.工件底部施加全自由度约束，左侧施加X方向位移约束.

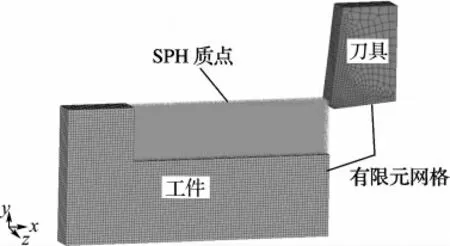
图2 超精密切削仿真几何模型Fig.2 Geometry model of ultra－precision cutting

光滑粒子与有限单元耦合的难点主要集中在光滑粒子区和有限单元区交界面处的计算.本文采用LS－DYNA 提供的点－面固连接触来实现两部分的耦合，将SPH 质点约束在网格上.

本文所采用的刀具角度及切削参数见表1.

2.2 材料模型

工件材料选择AISI4340钢.切削过程中工件将发生严重的塑性变形并伴随温度及应变率的变化.本文选择Johnson－Cook（JC）本构模型来作为工件的材料模型.该模型是von Mises塑性模型中的一种特殊形式，适用于金属材料的高应变率情况.如方程（4）所示，JC 本构方程可以反映切削过程中材料的流动应力：

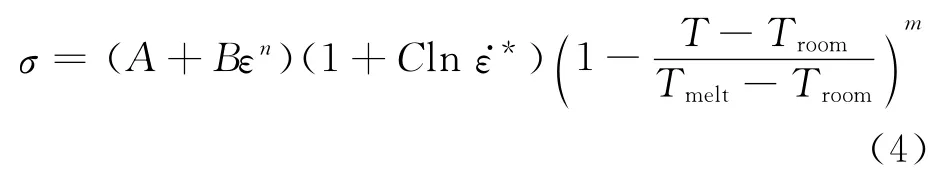
其中ε为等效塑性应变，ε·＊为等效塑性应变率，Troom为室内温度，Tmelt为融化温度.5个材料常数A、B、C、m和n分别为屈服极限、硬化模量、应变率敏感指数、热软化系数以及硬化系数［14］.工件材料本构参数见表2.

表2 工件材料本构参数Tab.2 Constitutive parameters of workpiece

由于金刚石刀具可以获得极锋利的切削刃，超精密切削一般使用金刚石作为刀具材料.考虑到其硬度比工件材料大得多，本文将刀具设置成刚性体，不考虑它在切削过程中的变形.目前超精密切削中采用的金刚石刀具切削刃钝圆半径一般为0.1～0.8μm，这里取切削刃钝圆半径为0.3μm.

3 仿真结果及讨论

3.1 切屑形成及应力分析

金刚石刀具刀刃钝圆半径对切屑形成和加工表面质量有重要影响.图3为初始阶段切削区域SPH 质点位移矢量图.图4特别追踪了切削深度内的6个质点的运动轨迹.从图中可以看出，起主要切削作用的是刀刃钝圆，切削层金属在其强烈推挤作用下发生分离，大部分被推挤到上方逐渐形成切屑，但底层部分材料被刀刃钝圆挤压而滑移到成形表面.因此超精密加工中实际切削厚度要小于理论切削厚度.

图3 切削区域SPH 质点位移矢量图Fig.3 Displacement vector of SPH nodes in cutting area

图4 切削层内6个SPH 质点运动轨迹Fig.4 Traces of 6SPH nodes in cutting layer

图5显示了切削速度v＝10 m／s，切削深度ap＝0.6μm 时不同时刻的等效应力分布情况.初始切入阶段最大等效应力主要分布于刀尖钝圆及剪切滑移带.在刀尖钝圆强烈的挤压作用下，内部应力达到工件材料屈服极限后，SPH 粒子开始发生不可逆变形，沿前刀面塑性流动从而形成切屑，可以形成连续带状切屑.稳定阶段最大等效应力主要分布于由刀尖钝圆向上切屑与前刀面的接触区.切削稳定阶段剪应力变化较为平缓，最大剪应力在840 MPa上下浮动，如图6所示.

图5 不同时刻等效应力分布Fig.5 Equivalent stress distribution for different time steps

图6 最大剪应力变化Fig.6 Variation of maximum shear stress

未观察到大的位错或裂纹，但由于刀具钝圆剧烈的挤压作用，切削层底部材料被向下推挤，生成一层致密的成形表面，表层粒子分布杂乱，应力分布较为复杂，如图7所示.成形表面下（d≈0.5 μm）可观察到较为严重的残余应力分布.这成为影响超精密切削表面质量的重要因素.

图7 成形表面残余应力分布Fig.7 Residual stress on formed surface

3.2 切削温度场分析

超精密切削中虽然切削深度很小，但切削过程中会产生大量的切削热.利用LS－DYNA 提供的热力耦合分析，只需添加材料相应热属性及热分析时间步长等，就可以对切削过程进行热力耦合计算.切削达到稳定状态后切屑的温度分布如图8所示.可以观察到几个层次分明的等温线.切屑的温度比工件温度高得多，意味着大部分的热量被切屑带走.从图中可以看出最高温度出现在刀尖钝圆半径的上端，靠近材料分离的发生点，这是由此处刀尖钝圆对切削层材料的强烈挤压以及切屑与前刀面之间的剧烈摩擦导致.切削达到稳定阶段后所获得的最高温度约为180℃.这与有限元模拟超精密切削得到的最高温度大致相同［15］.温度超过700℃时，金刚石刀具会出现明显的化学磨损，因此本文仿真条件下可以忽略刀具的磨损［16］.

为观察切削速度对温度的影响，进行了切削深度ap＝0.6μm 时不同切削速度的计算.图9显示了在不同切削速度下，切削达到稳定后切屑的最高温度.从图中可以看出，随着切削速度的增大，切削温度显著上升且上升的速度越来越快.这将增大金刚石刀具化学磨损的可能，并导致加工表面精度降低.

图8 切屑温度场云图（v＝10m／s，ap＝0.6μm）Fig.8 Temperature fringe levels of the chip（v＝10m／s，ap＝0.6μm）

图9 不同切削速度下的切削温度Fig.9 Temperature for different cutting speeds

3.3 塑性应变分析

如图10所示，在切削过程中，切屑发生塑性应变，并且从主变形区沿着剪切滑移带延伸至与前刀面的接触区，这是由于两者之间的剧烈摩擦所致.此外，由于受到刀尖钝圆的强烈挤压，成形表面也存在一层致密的塑性变形.最大塑性应变约为15.2，出现在刀尖钝圆顶点，与最高温度分布点相符.这说明切削热主要来源于切削层受挤压时塑性功的热转换.

图10 塑性应变分布Fig.10 Distribution of plastic strain

3.4 切削力分析

如图11所示，刀具与工件接触的初始阶段，随着接触应力的增大，切削力急剧上升，但接触应力达到材料屈服极限后切削力将小幅回落.之后随着切削层粒子在前刀面的堆积，切削力将继续增大.最终切削层粒子进入稳定的塑性流动阶段后，切削力在260N 小幅波动.而超精密切削实验中测得的切削力变化情况如图12 所示［15］.可以看出，模拟与实验得到的切削力变化趋势基本一致.

刀尖钝圆半径的大小对超精密切削有着重要影响.本文计算了同一切削用量（v＝10m／s，ap＝0.6μm）下钝圆半径为0.3μm 和0.6μm 时的切削力.图13所示为两种情况下对应的X、Y方向切削力分量对比.可以看出刀尖钝圆半径的增大会导致切削力的剧增，尤其以Y方向切削力即切削抗力增量较大.X方向切削力增大了23.5%，而Y方向切削力增大了166.7%.显然，切削抗力的增大会导致刀尖对成形表面的挤压，加剧加工硬化从而降低表面质量.

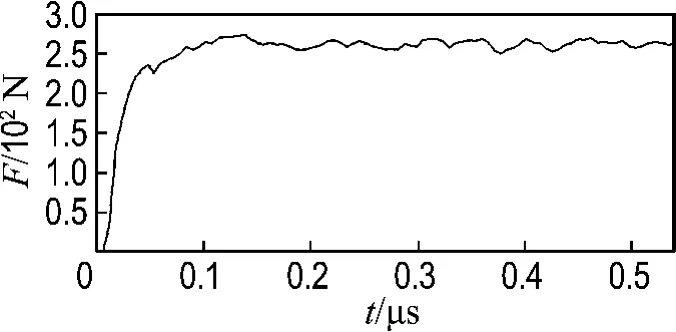
图11 切削力变化情况Fig.11 Change of cutting force

图12 实验测得切削力变化情况Fig.12 Cutting force variation in experimentation

图13 钝圆半径对切削力的影响Fig.13 Effect of edge radius on cutting force

4 结论

（1）将FEM 与SPH 法结合，建立超精密切削的FEM－SPH 耦合模型，有效避免了传统有限元方法处理大变形问题时出现的网格畸变问题.大变形区内SPH 粒子的“自然”流动可以理想地描述切屑的形成过程.

（2）刀尖钝圆起主要切削作用，刀尖的推挤导致切削层发生剪切滑移，SPH 粒子塑性流动而形成切屑.同时刀尖钝圆的强烈挤压导致形成了一层致密且残余应力严重的成形表面.

（3）切屑温度比工件高得多，大部分的切削热被切屑带走.最高温度出现在刀尖钝圆的顶点附近，这也与塑性应变的分布相符，说明大部分切屑热来源于切削过程中的塑性功转换.

（4）切削力随着SPH 粒子在前刀面的堆积而迅速上升，但SPH 粒子进入稳定的塑性流动阶段后，切削力在一稳定值附近小幅波动.增大刀尖钝圆半径将会导致切削力尤其是切削抗力显著增大.

［1］袁巨龙，王志伟，文东辉.超精密加工现状综述［J］.机械工程学报，2007，43（1）：35－48.YUAN Ju－long，WANG Zhi－wei，WEN Dong－hui.Review of the current situation of ultra－precision machining ［J］.Chinese Journal of Mechanical Engineering，2007，43（1）：35－48.（in Chinese）

［2］曾 刚，曾 攀.切削加工过程数值模拟的研究进展［J］.力学进展，2001，31：394－404.ZENG Gang，ZENG Pan.Advances in numerical simulation technology for cutting process ［J］.Advances in Mechanics，2001，31：394－404.（in Chinese）

［3］Guo Y B，Yen D W.A FEM study on mechanisms of discontinuous chip formation in hard machining［J］.Journal of Materials Processing Technology，2006，155－156：1350－1356.

［4］Lucy L B.A numerical approach to the testing of the fission hypothesis ［J］.The Astronomical Journal，1977，8（12）：1013－1024.

［5］Gingold R A，Monaghan J J.Smoothed particle hydrodynamics theory and application to non－spherical stars［J］.Monthly Notices of the Royal Astronomical Society，1977，181：375－389.

［6］Monaghan J J.Shock simulation by the particle method SPH［J］.Journal of Computational Physics，1983，52：374－389.

［7］李裕春，时党勇，赵 远.ANSYS10.0LS－DYNA基础理论与工程实践［M］.北京：中国水利水电出版社，2005：392－394.LI Yu－chun，SHI Dang－yong，ZHAO Yuan.Basic Theory and Engineering Practice of ANSYS 10.0LSDYNA ［M］.Beijing：China Water Power Press，2005：392－394.（in Chinese）

［8］Heinstein M，Segalman D.Simulation of orthogonal cutting with smooth particle hydrodynamics［R］／／Sandia National Laboratories Report.New Mexico：Sandia National Laboratories，1997.

［9］Limido J，Espinosa C.A new approach of high speed cutting：SPH method［J］.Journal de Physique IV，2006，134：1195－1200.

［10］王永刚.超精密切削切屑形成过程的SPH 方法模拟研究［J］.中国机械工程，2009，20（23）：2861－2864.WANG Yong－gang.SPH method simulation of chip formation in ultra－precision cutting processes［J］.China Mechanical Engineering，2009，20（23）：2861－2864.（in Chinese）

［11］Bagci E.3－D numerical analysis of orthogonal cutting process via mesh－free method ［J］.International Journal of the Physical Sciences，2011，6（6）：1267－1282.

［12］Kamoulakos A，Przybylowicz M，Groenenboom P.Smoothed particle hydrodynamics for space debris impact simulations– An approach with the PAMSHOCK transient dynamics code ［C］／／International Workshop in New Models and Numerical Codes for Shock Wave Processes in Condensed Media.Oxford：［s n］，1997

［13］宿 崇，唐 亮，侯俊铭.基于FEM 与SPH 耦合算法的金属切削仿真研究［J］.系统仿真学报，2009，21（16）：5002－5005.SU Chong，TANG Liang，HOU Jun－ming.Simulation research of metal cutting based on FEM and SPH ［J］.Journal of System Simulation，2009，21（16）：5002－5005.（in Chinese）

［14］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures ［C］／／Proceedings of the 7th International Symposium on Ballistics.The Hague：International Ballistics Committee，1983：541－547.

［15］翟元盛，梁迎春，王洪祥.圆弧刃精密切削实验及其三维有限元分析［J］.纳米技术与精密工程，2007，5（1）：72－77.ZHAI Yuan－sheng，LIANG Ying－chun，WANG Hong－xiang.Experimental and three dimensional finite element analysis on precision cutting for tool nose radius ［J］.Nanotechnology and Precision Engineering，2007，5（1）：72－77.（in Chinese）

［16］张元良，周志民，黄春英，等.天然金刚石振动与气体保护切削黑色金属技术研究［J］.机械科学与技术，2004，23（3）：339－342.ZHANG Yuan－liang，ZHOU Zhi－min，HUANG Chun－ying，etal.Diamond turning of ferrous metals by applying ultrasonic vibration and gas shield ［J］.Mechanical Science and Technology，2004，23（3）：339－342.（in Chinese）