马尔可夫模型在过程企业管道维修中应用

丛广佩，高金吉

（1.大连理工大学 化工学院，辽宁 大连 116024；2.北京化工大学 机电工程学院，北京 100029）

0 引言

基于风险的检验（RBI）是一种利用风险来确定设备定期检验范围和检验手段的检验优化方法，它利用一个简化后果计算将设备失效可能性转换为设备损伤带来的风险.API581第1版中将设备失效后介质的扩散面积作为后果，

是传统的安全后果考虑［1］，而在API581第2版中，则倾向于将设备失效后金融损失作为后果［2］，

它弥补了第一版中后果无法考虑经济损失、维修费用和环境影响的问题.

从中可以看出，RBI风险计算中后果只是一个常量，因此决定风险演变规律的是与时间有关的设备失效概率.在失效概率计算方面人们做了许多探索，Fleming开发了应用于核电管道系统中的失效可能性计算模型［3］，并在改进之后将其应用于二十多家核电厂在役检验策略的制定［4］.其中大部分方法都是基于统计方法的计算模型［5］.这种模型的缺点在于需要首先区分可能的失效机理及其关键参数，并将失效数据按照可能的机理和关键参数进行分类统计，否则应用该方法要么会由于数据划分不够而导致统计结果带有巨大的不确定性，从而使不确定性量化失去意义，要么会造成数据过于稀疏，使统计结果不具备统计规律［6］.此外，虽然通过历史数据统计出来的失效概率，可以反映之前的检验和维修活动对于失效概率的影响，但当检验或维修策略发生变化时，这种基于历史数据的统计估计可能将失去作用［7］.为此，人们将检验前的历史统计规律作为先验分布，而将检验结果作为条件概率，然后利用前人提出的贝叶斯方法［8］解决了这个问题.但应用这种方法的前提是损伤增量服从指数分布［9］，因此只能针对等时间间隔的检验和维修.van Noortwijk等吸取挡潮闸［10］和堤坝［11］的成功经验，提出了应用Gamma随机过程为损伤增量建模的方法［12］，但是为了简化贝叶斯方法的计算，必须令先验分布服从倒Gamma分布，这限制了该模型的应用.为了避免应用随机过程建模的复杂性，且要充分考虑检验和维修策略变更的影响，Fleming利用三状态马尔可夫模型对核电管道系统进行了建模，该模型将泄漏和破裂都作为管道失效形式加以考虑.但是中国石化企业的实际情况是针对泄漏问题会采用带压堵漏等复杂维修技术进行维修，这实际上是否定了泄漏作为失效模式三状态马尔可夫模型，鉴于此本文将试图建立一个适合中国石化企业的四状态管道失效模型.

1 马尔可夫模型

1.1 通用四状态马尔可夫模型

通用四状态马尔可夫模型如图1所示，它可以应用于多种在材料基材上的损伤，例如流体加速腐蚀、热疲劳等，甚至可以用于极端荷载条件下的失效，比如水击和超压.

图1 通用四状态马尔可夫模型Fig.1 General four－state Markov model

根据图1，与时间有关的四状态微分方程组［13］为

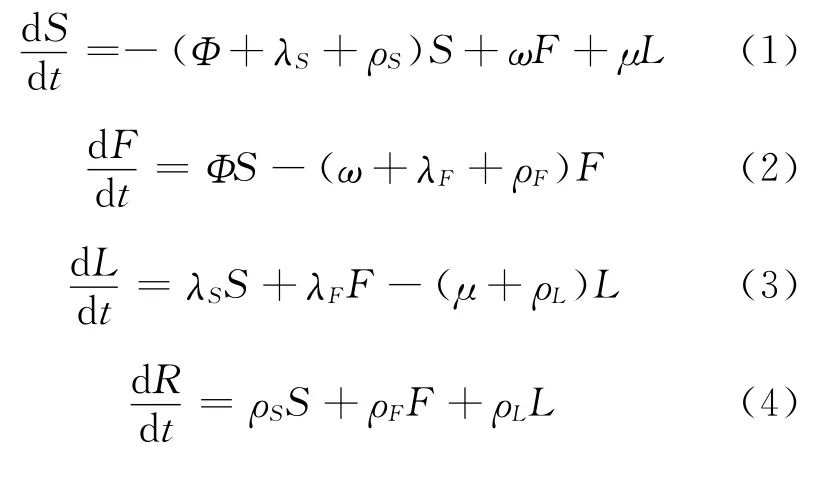
且四种状态的概率关系为

若破裂作为唯一的失效状态，则根据以上方程定义了四状态可靠率为

灾害率的微分方程［14］为

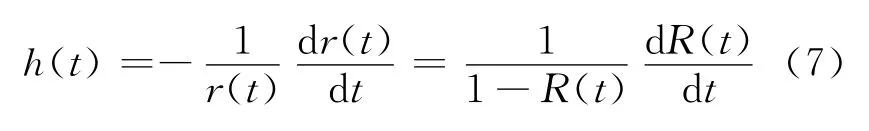
1.2 基于LBB的四状态马尔可夫模型

LBB模型是一种允许泄漏情况发生的失效模型.虽然原则上石化企业一般不允许泄漏，但在中国的石化企业中通常针对泄漏采取带压堵漏、碳纤维布加环氧树脂等办法，往往可以实现泄漏不停车，因此中国石化企业的这种维修等于将石化设备管道的失效看作LBB 模型.据此，更加适合中国石化企业的马尔可夫模型应为如图2所示的四状态马尔可夫模型.

图2 LBB失效四状态马尔可夫模型Fig.2 LBB failure four－state Markov model

根据图2所示的模型，式（1）～（4）中的ρS、ρF为零，则式（1）～（4）变为

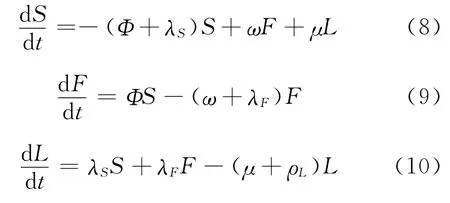
令X＝（SFLR）T，

则式（8）～（11）的矩阵形式为

且边界条件为

则根据常系数微分方程的解法，式（12）的解为

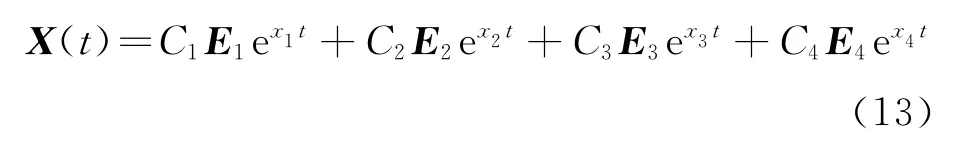
其中C1、C2、C3、C4为由边界条件确定的系数；E1、E2、E3、E4为G的特征向量，且E4＝（0 0 0 1）；x1、x2、x3、x4为G的特征值，且x4＝0；x1、x2、x3是下面特征方程的解：

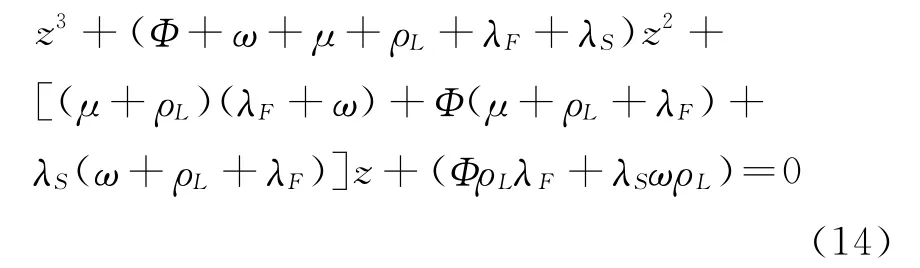
式（14）所示的三次方程可用盛金公式［15］求解.

2 马尔可夫模型的参数估计

2.1 中间参数的估计

2.1.1 在不同后果情况下，缺陷被检验的平均概率 按照RBI的思想，管道在其寿命周期内会根据其风险的变化而经历不同的检验策略，因此本文用这些检验的均值有效率来代表该管道的缺陷检出率.根据文献［1－2］中对于失效可能性等级的定义，假设对高风险和中高风险进行高有效性检验，对中风险且失效可能性等级大于等于3的进行通常有效性检验，而对低于3的进行一般有效性检验，对低风险不进行检验，且各种检验情况的检验效率符合文献［1－2］提供的离散概率分布数据，并得到如图3所示的设备风险矩阵.

从图3可以看出不同的先天后果等级，设备在寿命周期内所经历的检验效率的变化也不同，因此，得到按照不同后果等级的缺陷被检验出的平均概率，如表1所示.

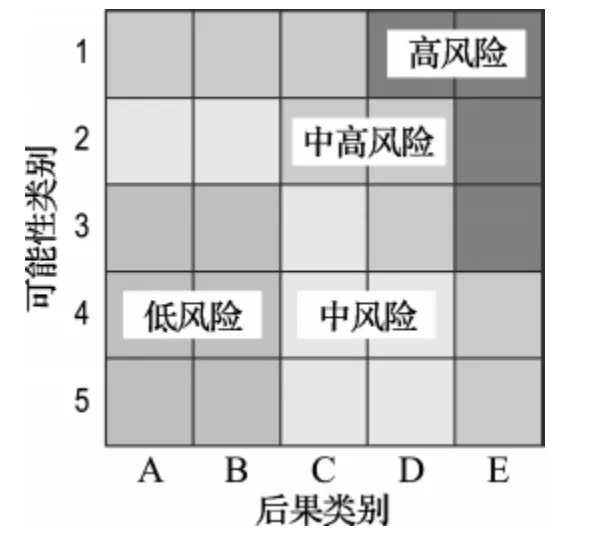
图3 设备的风险矩阵Fig.3 Risk matrix of equipment

表1 在不同失效后果情况下缺陷被检验出的平均概率Tab.1 Average probability of flaw inspected in different failure consequences

2.1.2 在检验部位、检验手段确定情况下检出缺陷存在的概率pid令pid为缺陷可被检验手段识别的概率，x（t）为在t时刻的损伤总量，且x（t）服从Gamma随机过程：

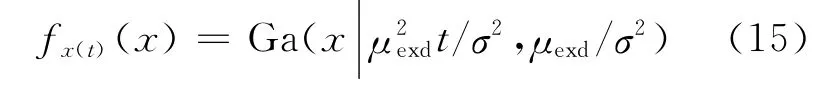
其中

并令

在T时刻，选取的损伤总值作为随机变量数据，计算T时刻的数学期望和偏差，并按式（16）计算平均损伤率和平均损伤率的偏差，代入下式得到在T时刻的总损伤值的Gamma随机分布：

令ε0为检测设备的测量精度，则当x（t）＞ε0时，该缺陷是可以识别的，因此根据式（18）得

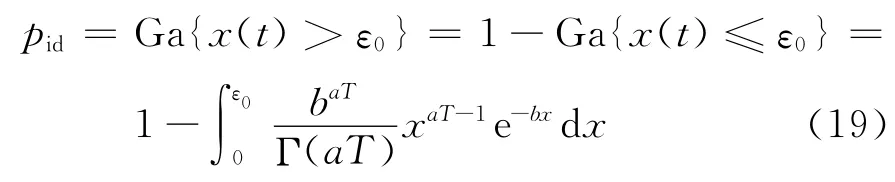
2.1.3 其他中间参数 令发生泄漏时管道的运行时间为τl，在役维修所需时间为τr，从当前管道泄漏时刻到下次预防性或预知维修时间间隔为τp，则在维修期间其他非维修部位发生泄漏的概率pis服从泊松分布：

则到预防性或预知维修时间其他非维修部位发生泄漏的概率pp服从泊松分布：

则在泄漏情况下发生一次有效在役维修的概率

其中为在役维修工艺（如带压堵漏）不导致管道失效的概率；Tld为泄漏探测的时间间隔；pld为泄漏探测有效率.

在役维修所需时间为τm，在发生一次有效维修情况下，发生有效停车维修的概率

令τld为检漏时间，从可探测缺陷状态下，进入泄漏状态的概率pw为

其中w为壁厚.

令设备超压服从对数正态分布，则设备在完整条件下的超压概率pop为

其中pl为压力荷载.

泄漏探测有效率pld为

其中τd为一次泄漏探测所用去的时间；Pldm为某一失效后果下的均值泄漏探测有效率，各种泄漏探测手段的探测有效率如表2所示，则不同失效后果下的Pldm与其对应的缺陷被检验的平均概率一样，如表1所示.

表2 不同泄漏检验手段的探测效率Tab.2 Detecting effectiveness of different leak detection means

2.2 马尔可夫参数

在泄漏情况下发生一次有效维修率

在缺陷条件下的维修率

其中pf为缺陷失效的概率.

从完整状态进入可探测缺陷状态的转换率

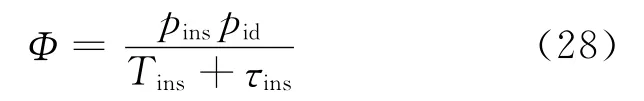
其中τins为检验时间；Tins为检验时间间隔.

从可探测缺陷状态下，进入泄漏状态的概率

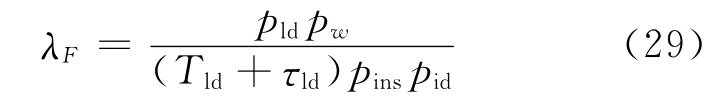
其中：τld为检漏时间.

从可探测泄漏态下，进入破裂状态的概率

从完整或无可探测缺陷状态下，进入泄漏状态的概率为

3 算 例

某石化管道发生穿孔，其具体情况为管道内径200mm，设计壁厚6mm，5a穿孔，以除泄漏点外，最薄点壁厚（1.1mm）计算，平均腐蚀速率为1mm／a，泄漏点附近最薄处为1.6 mm，平均腐蚀速率为0.88mm／a，弯头厚度为4mm，原始厚度为8mm，泄漏发现方式为人工巡检，巡检周期为3h一次，每次用时1h，RBI结果为高风险，设备后果等级为D 级，并且令μf＝0.99.

则根据式（15）～（31），本文提出的马尔可夫模型的参数及中间参数如表3所示.

表3 LBB马尔可夫模型参数的计算结果Tab.3 Results of case based on LBB Markov model

将表3中的马尔可夫参数代入式（6）、（13）和（14），得出在对该管道进行包括带压堵漏技术在内的复杂维修时，该管道的可靠度为

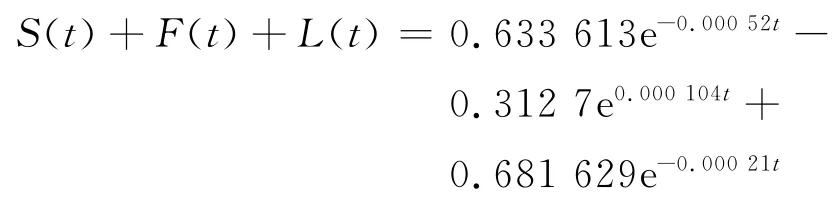
再由式（7）得，该管道的灾害率为

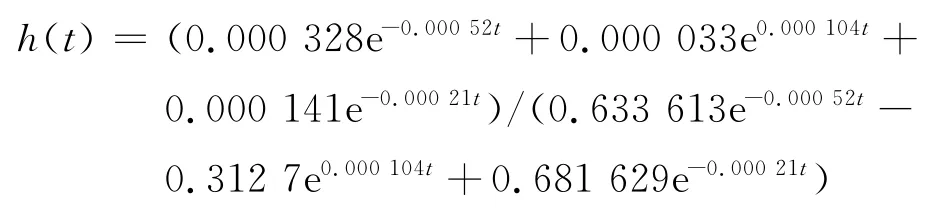
40a（设备的最高使用年限）破裂所导致的灾害率（设备失效率）变化曲线如图4所示.

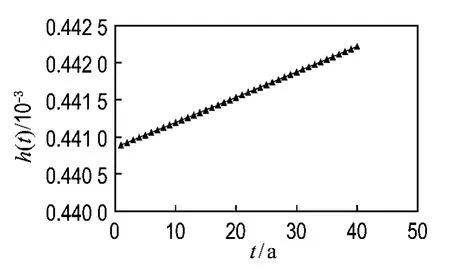
图4 破裂所导致的灾害率变化曲线Fig.4 Hazard rate curve caused by rupture

由图4可知，基于风险的检验、检漏，并在泄漏后对管道进行全面测厚的基础上，在设备寿命期内，采用包含带压堵漏技术的复杂维修过程，可以将该管道发生破裂并导致严重损伤的概率控制得很低，结合其D 级失效后果等级，按式（1）计算，则该管道的安全风险被控制在0.44～4.42m2.根据文献［2］，属于可以忍受的中风险级别.同时图4中灾害率呈逐年增加的趋势，该趋势反映了石化设备维修为非完全恢复性维修的特点.

4 结语

在以往的石化管道马尔可夫模型中通常采用三状态马尔可夫模型，即将泄漏和破裂统统作为失效来看待，但是在中国石化企业中通常会采用包含带压堵漏等技术的复杂维修过程，这种维修过程并不承认泄漏是设备失效的表现形式，反而更加符合允许泄漏发生的LBB失效模型，因此本文建立了基于LBB 的马尔可夫模型用以综合考虑泄漏非停车维修过程的影响，模型中认为存在一个维修过程在泄漏发生时将设备或管道维修回完好状态，更加适合中国石化企业管道的维修定量评估.从算例中可以看出在对管道进行全面测厚的基础上，复杂维修过程可以有效避免管道的破裂发生，而且马尔可夫模型的计算是一个设备失效概率随时间变化逐年增加的函数，正确地反映了石化设备维修为非完全恢复性维修的特点.从而证明本文提出的基于LBB 的四状态马尔可夫模型不但可以定量估算中国石化企业维修过程的风险控制效果，而且还能从时间上推演出非完全恢复性维修过程对设备失效概率的影响.

［1］American Petroleum Institute.API 581Risk－Based Inspection Base Resource Document ［S］.Washington D C：API，2000.

［2］American Petroleum Institute.API 581Risk－Based Inspection Technology［S］.Washington D C：API，2008.

［3］Fleming K N.Piping system reliability and failure rate estimation models for use in risk informed inservice inspection applications ［R］／／EPRI TR－110161.Palo Alto：EPRI，1998.

［4］Fleming K N，Hutchinson J J.Risk informed inservice inspection of the ComEd nuclear plants［C］／／Proceedings of PSAM 5.Osaka：PSAM，1999：98－104.

［5］Gosselin S R，Fleming K N.Evaluation of pipe failure potential via degradation mechanism assessment［C］／／Proceedings of ICONE 5.Nice：ICONE，1997：26－30.

［6］Chapman O J V，Fabbri L.Discussion Document on Risk Informed In－service Inspection of Nuclear Power Plants in Europe ［M］.Petten：European Commission，2000.

［7］Fleming K N，Lydell B O Y.Database development and uncertainty treatment for estimating pipe failure rates and rupture frequencies ［J］.Reliability Engineering ＆ System Safety，2004，86（3）：227－246.

［8］van Noortwijk J M，Cooke R M，Matthijs K.A Bayesian failure model based on isotropic deterioration［J］.European Journal of Operational Research，1995，82（2）：270－282.

［9］van Noortwijk J M，van der Weide J A M，Kallen M J，etal.Gamma processes and peaks－overthreshold distributions for time－dependent reliability［J］.Reliability Engineering ＆System Safety，2007，92（12）：1651－1658.

［10］van Noortwijk J M，Klatter H E.Optimal inspection decisions for the block mats of the Eastern－Scheldt barrier［J］.Reliability Engineering＆System Safety，1999，65（3）：203－211.

［11］Speijker L J P，van Noortwijk J M，Kok M，etal.Optimal maintenance decisions for dikes ［J］.Probability Engineering Information Science，2000，14（1）：101－121.

［12］Kallen M J，van Noortwijk J M.Optimal maintenance decisions under imperfect inspection［J］.Reliability Engineering ＆System Safety，2005，90（2－3）：177－185.

［13］Fleming K N.Markov models for evaluating riskinformed in－service inspection strategies for nuclear power plant piping systems ［J］.Reliability Engineering and System Safety，2004，83（1）：27－45.

［14］Shooman M L.Probabilistic Reliability：An Engineering Approach ［M］.2nd ed.Malabar：Krieger Publishing Company，1990.

［15］范盛金.一元三次方程的新求根公式与新判别法［J］.海南师范学院学报：自然科学版，1989，2（2）：91－98.FAN Sheng－jin.A new extracting formula and a new distinguishing means on the one variable cubic equation［J］.Journal of Hainan Teachers College：Natural Science，1989，2（2）：91－98.（in Chinese）