基于数字全息及复用技术的全场偏振态测试方法*

马骏1)袁操今2)† 冯少彤2)聂守平2)

1)(南京理工大学电子工程与光电技术学院,南京 210094)

2)(南京师范大学物理科学与技术学院,南京 210097)

1 引言

除了振幅、相位、相干长度和光谱信息以外,偏振态也是描述光波波前特征的参量之一.对于光波波前参量的调控,可以实现某些特殊效果,例如,改变光波的相位分布可以实现相衬成像[1];改变光波的偏振态可以实现偏振成像[2]等.常规偏振光如线偏振光、椭圆偏振光或圆偏振光具有偏振态与空间位置不相关特性,而矢量光束是一种偏振态时变且与局部空间位置相关的特殊偏振光.由于矢量光束所具有的独特性质,使得其近年来在显微成像、非线性光学、光通信和生物光子学等领域得到了广泛应用,并且获得了一些十分有意义的结果[3-6].在这些应用中,产生和测试特定偏振态的矢量光束是至关重要的.考虑到矢量光束时变性和空间相关性特点,目前急需获得一种实时、全场探测的测试方法.

利用波片及偏振片组合是实验室进行波前偏振态检测的常规方法,同样也是商用偏振态检测设备的典型方案.然而,常用的偏振态检测设备仅可以提供被测波前在传播方向上固定测试位置处的偏振信息.且由于测试方法不具备二维采样特性,因此不能用来进行整个波面的实时检测.数字全息术是一种可以同时记录被测波前振幅和相位信息,并能数值重构这些信息的技术[7,8],它的出现为实时二维检测光束偏振态提供了可能性.通过用两个偏振方向互相正交的线偏振参考波前与被测波前进行干涉,可以分别记录并重构被测波前两个正交方向上的复振幅信息[9-11].Yokota等[12-14]提出了利用光纤法拉第旋转器顺序调制参考光偏振态,通过CCD同步控制可以采集到两个垂直偏振态方向参考光和物光干涉得到的全息图,虽然装置简单,但旋转器的误差难以消除,而且不能进行实时记录.除此以外,在同轴数字全息中通过使用一束线性偏振参考光和一束椭圆偏振参考光的方法也能够获取测试光波的斯托克斯参量[15],但需要多次记录.对于实时偏振态检测,双参考光的数字全息术被认为是一种可靠的方法.同时,数字全息技术与偏振成像相结合已经在多个领域得到了应用,例如3D成像[16]、光纤双折射测量[17]、散斑噪声抑制[18]、移相等[19].

本文采用了偏振和角分复用技术融入数字全息系统的方法,实现实时、全场偏振态的检测.偏振复用技术保证被记录的两个相互正交的物光分量不会发生相互干涉;而角分复用技术可以利用参考光载频的不同将两个分量在频谱面上进行分离.本文通过实验证明,利用全息再现得到的物光在两正交方向复振幅信息,可以实时构建被测光束的斯托克斯参量的四个分量以及琼斯矢量.同时,为了证明本文方法的可靠性,利用数字全息数值再现计算的特点,对不同再现距离处的偏振态进行了分析.

2 实验装置

实验中用到的光路是一个自行搭建的改进型马赫-曾德尔干涉系统,如图1所示.其中,光源是波长为532 nm的半导体激光器,出射光束为线偏振光,经过扩束准直后,形成一束平面波.通过旋转起偏器P1的角度,可以自由调整入射光波的强度和偏振方向.平面波通过分束镜(BS1)被分为两束光,一束光是物光,另一束是参考光.在参考光光路中,光波经过偏振分束镜(PBS)后,进一步被分成两束偏振方向相互正交的线偏振参考光.为了将两束参考光波的强度比控制为1:1,以避免两再现像振幅的差异,我们在BS1和PBS之间插入一个半波片(HWP),通过旋转半波片,可以改变入射光的偏振方向,进而实现对两束参考光光强比的控制.在图1中,利用双向箭头和点表示两个相互正交的偏振方向.在物光光路中,物波经BS1和M1反射后依次透过起偏器P2和四分之一波片(QWP),可以产生测试偏振光.两参考光的入射角分别由反射镜M2和M3控制,通过改变二者角度为两正交偏振态的参考光叠加不同载频,进而使物光两正交分量在全息图频谱面上相互分离.两个正交偏振参考光束分别与物光正交分解后同方向的分量相干涉.由此看出,偏振态的全局坐标选取是由参考光决定的.

图1 实验装置示意图

3 理论分析

具有不同载波频率且偏振方向相互正交的两束参考光束,可以利用琼斯矢量表示为

式中ϕrx和ϕry是参考光束x,y方向上的初始相位,fx和 fy分别是x和y方向上的载波频率.

入射平面波依次通过一个起偏器和一个四分之一波片后,作为被测物光,其复振幅分布为[20]

式中Eox和Eoy是入射光波在x和y方向上两个分量的振幅,JR(λ/4)和Jp2(θ)分别是四分之一波片和起偏器的琼斯矩阵,Ox和Oy分别是通过两个器件后光波在两正交方向的分量.从这个方程中可以看出,这两个方向分量的相位差是π/2,并且由此可知,x,y方向上的振幅分量是由Eox,Eoy以及起偏器起偏方向与波片快轴方向的夹角θ决定的.

全息图是由物光和两束参考光相干涉产生的,其强度分布为

由于偏振方向相互垂直的光波不会发生干涉,因此在(3)式中直接将这些项略去.从(3)式可以看出,利用偏振复用技术能够分别得到x和y两个方向上的分量,而且可以同时记录,并不发生相互干涉.为了在全息图频谱面中将被记录的两个分量分开,在记录中利用角分复用技术,即通过控制参考光的载波频率将记录到的信息分开.在全息图的频域中通过选择合适的滤波窗口,可以获得如下两项:

由于参考光的载波频率 fx和 fy可以从全息图的频谱图分布上计算得到,因此,在数值再现中,将(4)和(5)式分别乘以exp[-i2πfyy]和exp[-i2πfxx],便可以消除 fx和 fy.但是由于难以准确获得两束参考光波的初始相位ϕry和ϕrx,不能通过数字校正的方法消除二者对测量带来的误差.因此,为了获得准确的实验结果,在全息记录前就需要对两者进行预标定.利用白光光源对两束参考光的光程进行调整,当观察到白光干涉条纹,可以最大程度地使两参考束光的初始相位相等.

将消除了参考光载频的物光复振幅分布进行衍射计算,可以分别获得距离记录面ZI处物光两个分量的复振幅分布,本文采用菲涅耳衍射近似公式:

利用数值重构获取x和y方向分量的复振幅Cx(xI,yI)和Cy(xI,yI)后,它们的强度和相位也都可以很容易地计算得到.将x和y分量的强度值相加和相减分别得到待测光波斯托克斯参量的前两个参数S0及S1,而利用两分量的振幅和相位之间的关系,可以进一步得到参量的后两个参数,即

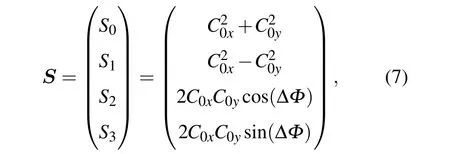
(7)式中ΔΦ是被测波面水平(x方向)和垂直(y方向)方向上的相位差.

除了利用斯托克斯参量外,琼斯矢量也可以描述物光的偏振态,琼斯矢量可以表示为

4 实验结果与分析

图2(a)和(b)为实验记录到的全息图及其局部放大图像.全息图的频谱示于图2(c)中.待测物光波x和y分量的虚像在图中用红色圆圈标注,由于它们在频域内彼此分离,通过数值滤波设计合适的滤波窗口,滤出红色圆圈内的频率成分信息,再进行逆傅里叶变换,可以得到两分量的复振幅.为了确定重构的准确距离,实验中在物光路中插入一个圆形光阑.

图2 实验结果 (a)全息图;(b)局部放大全息图;(c)图(b)的频谱

当再现距离ZI等于196 mm处,利用(6)式可以分别计算得到x和y分量的复振幅,对它们进行取模的平方和取幅角运算,可以进一步得到它们的强度和相位分布,如图3所示.图3(a)和(b)所示分别为x分量的强度和相位分布,y分量的强度和相位分布如图3(c)和(d)所示.由于光学元件表面存在疵病,特别是经过扩束之后,噪声也被放大,加之光阑的位置并非准确位于高斯光斑的中心,造成了两个分量的强度和相位均出现分布不均的情况.而在两个分量的相位差分布中,如图4(a)所示,这一不均匀的情况得到了很好的抑制.其中心部分两个分量相位差的平均值为92.36◦,与理论值90◦非常接近.由于空气扰动、光源出现随机相位漂移、四分之一波片的制作误差,以及即使利用白光对两束参考光初始相位进行标定,也不可能完全保证它们的初始相位完全相等,这些因素的共同影响带来了测量误差.从图4(b)显示的之差的分布,可见物波的x和y分量的振幅是不相等的.的分布也就是斯托克斯参量中S1分量,S0分布如图4(c)所示.限于篇幅,其他两个斯托克斯参量未在文中一一说明.通过求解得到物波x和y分量的振幅之后,可以进一步通过变换得到物波的琼斯矢量.

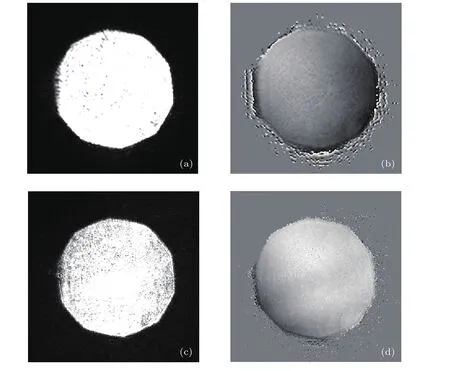
图3 x,y分量的强度及相位分布 (a)Cx的强度分布;(b)Cx的相位分布;(c)Cy的强度分布;(d)Cy的相位分布

图4 (a)相位差ΔΦ;(b)斯托克斯参量S1;(c)斯托克斯参量S0

为了验证该检测方法的可靠性,将再现距离分别增加四分之一、二分之一和四分之三波长,求出它们的复振幅.从图5给出的x方向四幅相位分布图看到,随着光程的改变,它们的相位出现了明显的变化.但是x方向与y方向的相位差在不同再现距离基本相等,均方差为0.35◦.由此可见,该检测方法具有一定可靠性.

图5 不同再现距离处x分量相位分布 (a)ZI=196 mm;(b)ZI=196 mm+λ/4;(c)ZI=196 mm+λ/2;(d)ZI=196 mm+3λ/4

5 结论

本文介绍了一种基于离轴数字全息术的实时、全场偏振测试方法.实验系统可以同时获取物光光波水平和竖直分量的复振幅分布.由于采用了偏振复用技术,保证了被记录的两个相互正交的物光分量之间不发生干涉;由于引入了角分复用技术,两个参考光波引入的倾斜载频不同,记录的两分量信息可以彼此分离并分别重构.控制参考光的入射角度及偏振方向,不仅能实现再现像的分离,而且能够设定偏振参量的全局坐标系.本文通过实验证明利用该方法可以实时获取物波全场斯托克斯参量和琼斯矢量,并且可以获取光波在轴上不同位置处的偏振态.该方法可以进一步应用于双折射物体运动轨迹成像、矢量偏振显微超分辨等领域.

[1]Teschke M,Sinzinger S 2009 J.Opt.Soc.Am.A 261015

[2]Demos S G,Alfano R R 1997 Appl.Opt.36150

[3]Lerman G M,Stern L,Levy U 2010 Opt.Express 1827650

[4]Beckley A M,Brown T G,Alonso M A 2012 Opt.Express 209357

[5]Pu J X,Wang T,Lin H C,Li C L 2010 Chin.Phys.B 19089201

[6]Zhao W Q,Tang F,Qiu L R,Liu D L 2013 Acta Phys.Sin.62054201(in Chinese)[赵维谦,唐芳,邱丽荣,刘大礼2013物理学报 62054201]

[7]Mann C,Yu L F,Lo C M,Kim M 2005 Opt.Express 138693

[8]Cuche E,Marquet P,Depeursinge C 1999 Appl.Opt.386994

[9]Colomb T,Dahlgren P,Beghuin D,Cuche E,Marquet P,Depeursinge C 2002 Appl.Opt.4127

[10]Ohtsuka Y,Oka K 1994 Appl.Opt.332633

[11]Colomb T,Cuche E,Montfort F,Marquet P,Depeursinge C 2004 Opt.Commun.231137

[12]Yokota M,Terui Y,Yamaguchi I 2006 Opt.Rev.13405

[13]Yokota M 2008 Appl.Opt.476325

[14]Yokota M,Terui Y,Yamaguchi I 2007 Opt.Eng.46055801

[15]Chen P,Tang Z L,Wang J,Fu X D,Chen F H 2012 Acta Phys.Sin.61104202(in Chinese)[陈萍,唐志列,王娟,付晓娣,陈飞虎2012物理学报61104202]

[16]Nomura T,Javidi B,Murata S,Nitanai E,Numata T 2007 Opt.Lett.32481

[17]Colomb T,Dürr F,Cuche E,Marquet P,Limberger H G,Salath´e R P,Depeursinge C 2005 Appl.Opt.444461

[18]Rong L,Xiao W,Pan F,Liu S,Li R 2010 Chin.Opt.Lett.8653

[19]Nomura T,Murata S,Nitanai E,Numata T 2006 Appl.Opt.454873

[20]Goldstein D 2003 Polarized Light(2nd Ed.)(New York:Marcel Dekker,Inc.)p211