空间单位区域双二次有理贝赛尔曲面混沌特性研究

2013-10-24于万波周洋

物理学报 2013年22期

于万波周洋

(大连大学信息工程学院,大连 116622)

1 引言

目前,混沌现象的研究仍然在继续,从发现混沌现象到对混沌进行数学描述,从混沌控制到混沌同步再到系统的混沌化,研究人员一直在混沌的各个分支领域进行研究,取得了许多有价值的结果[1-8].系统混沌化是目前混沌领域的研究热点问题之一,通过修改系统的参数或者重新构造系统等使其出现混沌.混沌化的研究可以产生混沌序列用于图像加密等,也可以利用产生的混沌系统进行液体气体混合等实际工作领域.基于混沌本质的探索以及混沌化的需要,文献[9—15]对混沌的本质以及混沌化的一些方法进行了研究,给出了一些混沌化的新方法.文献[16]研究了调整小波函数使其混沌化的问题,文献[17]研究了平面单位区域内二次函数的混沌特性,得到的结论是标准二次映射是Li-Yorke混沌的,也是Devaney混沌的.事实上,在满足一定条件的情况下,还存在大量的二次函数是混沌的.二次函数都可以使用平移与缩放等变换化为标准二次函数,其混沌特性不变.对单位区域上的非标准二次函数进一步研究发现,可以使用平移与缩放的方法把非标准二次函数转化为标准二次函数或者亚标准函数,转化前后其混沌特性是不变的,即其迭代序列的震荡特性是相同的.另外,一个满射函数和单位区域内标准函数复合后仍然是单位区域内标准函数,这样,就可以把所有的二次函数变换到单位区域中进行研究,研究范围可以缩小到单位区域中来.单位区域内的标准函数是重要的,既是研究混沌的本质,也是研究混沌化的方法,文献[18—20]就是研究混沌化方法,并利用混沌化的方法产生序列进行图像加密等,所以该类问题有必要深入研究.

本文工作是文献[16,17]中研究工作的继续,是在曲线研究的基础上继续研究单位区域内曲面的混沌特性.

2 使用双二次有理贝赛尔曲面构造函数

鉴于函数图像的几何形状与混沌特性有直接关系,又因为有理贝赛尔曲面的控制点可以调整曲面的形状,所以使用有理贝赛尔参数曲面来研究曲面函数的混沌特性.作为有理贝赛尔曲面的一个特例,双二次有理贝塞尔曲面定义如下:

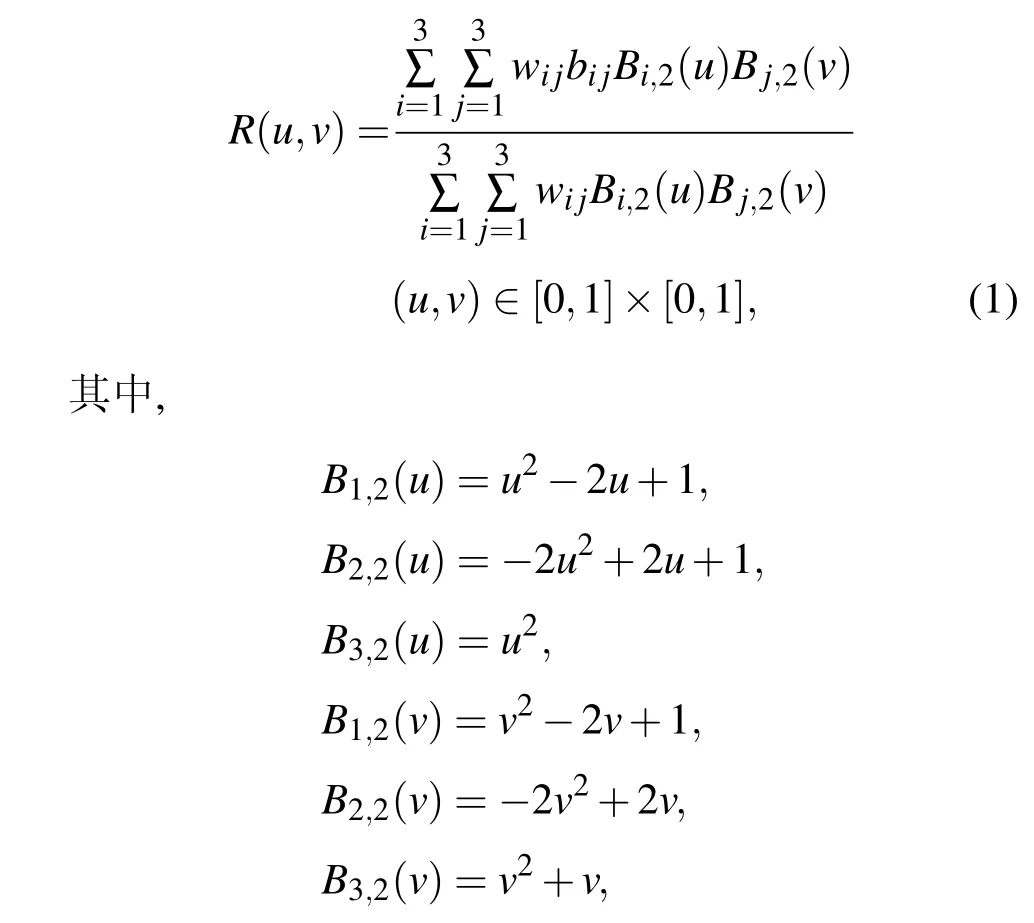
wi,j是权值,用来决定曲面的细节形状(例如,这些参数可以确定该曲面的截面是抛物线、椭圆或者双曲线等);bi,j是控制点,用来决定曲面主体结构形状;双二次有理贝塞尔曲面的变量x,y,z中的每个变量都需要9个控制点,然后由x,y,z构成空间曲面,是不超过4次的曲面.

在迭代过程中,如果使用x,y,z表示曲面,把u,v用x,y表示难度比较大,不易于实现迭代操作,所以在本文中直接使用u,v作为自变量进行研究.研究用的迭代表达式为

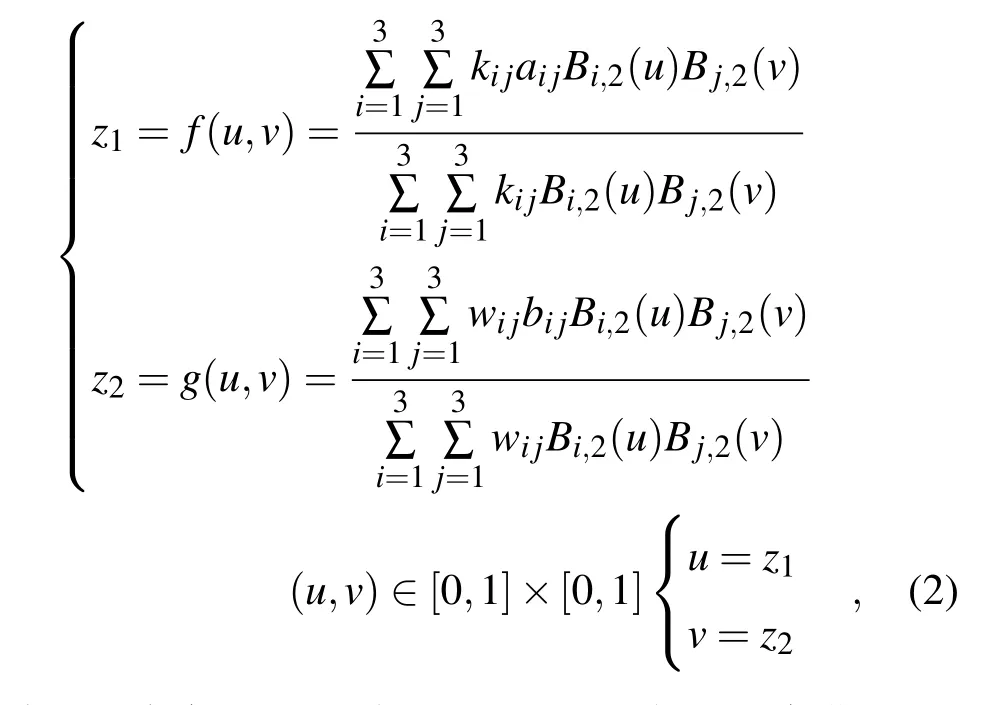
在(2)式中,f(u,v)与g(u,v)分别表示两个曲面,u,v为自变量,定义域为[0,1]×[0,1],根据有理贝塞尔曲面的定义,当9个控制点为(0,0,0),(0,0.5,0),(0,1,0),(0.5,0,0),(0.5,0.5,m),(1,0,0),(1,0.5,0),(1,1,0)时,曲面的形状如图1(b)所示,四条边界都在坐标轴上,图形向上凸起,最大值为1.其中

我们称这种曲面为单位区域内的标准双二次有理贝塞尔曲面.

研究发现,当(2)式中的两个曲面有一个是标准双二次有理贝塞尔曲面,另外一个曲面限制在单位区域内,迭代式(2)极易出现混沌.下面对这类曲面函数迭代进行研究.

3 单位区域内标准双二次有理贝塞尔曲面迭代研究

随机产生参数 kij与 wij,i=1,2,···,9,j=1,2,···,9,利用(3)式计算m,构造一个单位区域内的标准双二次有理贝塞尔曲面;然后随机生成控制点bij,i=1,2,···,9,j=1,2,···,9,构造另外一个二次曲面,两个二次曲面构成迭代表达式.利用该表达式进行迭代,平均每迭代7,8次就可以出现一个混沌,说明在单位区域的有理数中,混沌的参数要占七分之一或者八分之一,这一数据是巨大的.

下面选择有代表性的三个进行研究.

随机生成的第一个曲面的权值参数以及第二个函数曲面参数如下:

迭代表达式(1)的参数

迭代表达式(2)的参数

迭代表达式(3)的参数

这些参数对应的图形以及迭代后的吸引子图形如图1—3所示.

图1到图3在迭代的过程中,都是从u=0.3,v=0.6开始的,那么如果从其他的u,v开始迭代,是否也会出现类似的(近似)吸引子图形呢？让u与v都从0.01开始,迭代到0.99,步长为0.01,嵌套循环;对于每个u,v,迭代600次,去掉前100次,绘制后500次得到的点,结果绘制出的(近似)吸引子图形如图4所示,其形状与图1至图3基本相同.这也说明了吸引子是不与初始迭代值有关的.

图1 迭代表达式(1)的曲面与吸引子 (a)吸引子;(b)标准曲面;(c)随机生成的曲面

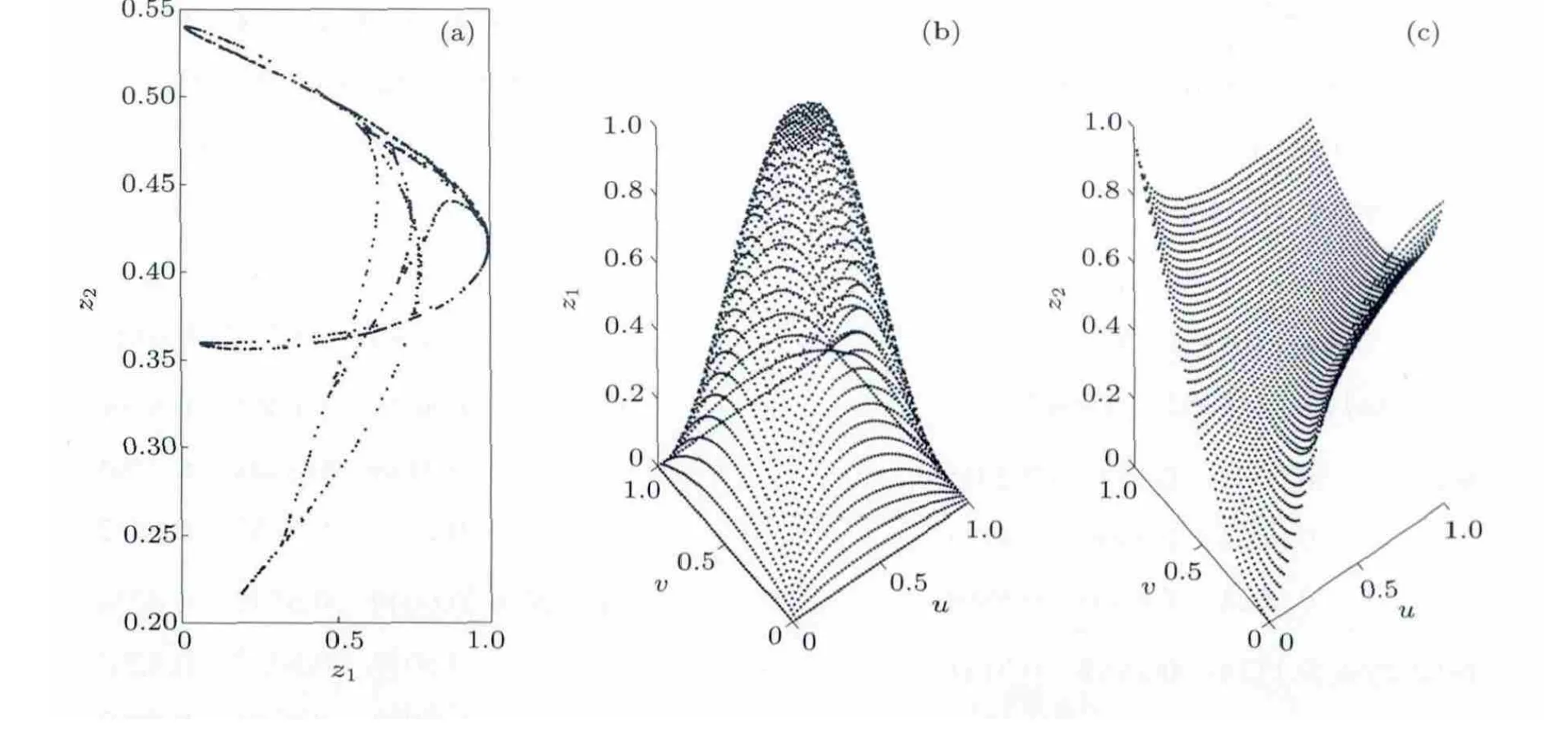
图2 迭代表达式(2)的曲面与吸引子 (a)吸引子;(b)标准曲面;(c)随机生成的曲面

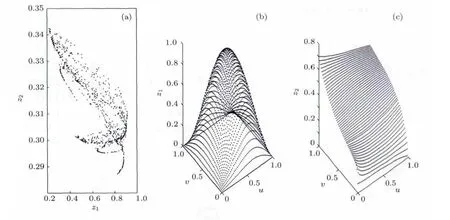
图3 迭代表达式(3)的曲面与吸引子 (a)吸引子;(b)标准曲面;(c)随机生成的曲面

为了更好研究上面迭代式的混沌特性,进一步绘制并观察其分岔图,如图5是迭代式(2)当w(2,3)变化时的分岔图.

通过大量的实验观察,第一个迭代表达式关于k和w的分岔图都有一定的混沌区间,如表1所示.当其他参数不变的情况下,k(1,1)在1.5到4之间变化时,分岔图呈现出混沌状态;其他参数不变的情况下,w(1,1)在-1到0之间变化时,分岔图呈现出混沌状态.

表1 迭代表达式(1)的参数分岔区间

图4 多个u,v绘制的吸引子 (a)迭代表达式(1);(b)迭代表达式(2);(c)迭代表达式(3)

图5 迭代式(1)当w(2,3)变化时的分岔图 (a)z1分岔图;(b)z2分岔图

图6 迭代曲面与吸引子(迭代式(1)参数k(2,2)变为10)(a)吸引子;(b)标准曲面;(c)随机生成的曲面

利用表1,可以得到更多的混沌表达式,例如k(2,2)=10时,迭代表达式(1)其他参数不变,绘制出的吸引子以及其函数图形如图6所示,函数图形与图1(b)相比,函数图形上部变平了而下部变陡;与图1(a)相比,吸引子形状也有改变.

迭代表达式(2)的参数分岔区间如表2所示.

从分岔图的形状上看,迭代表达式(2)的分岔图与迭代表达式(1)的分岔图有些区别,当w(2,3)变化时迭代表达式(2)的分岔图如图7所示.

利用表2,根据分岔图上的混沌区间可以构造出很多新的分形图,例如当w(2,3)=-0.3,其他参数不变时,绘制出的曲面图以及吸引子图形如图8所示.

表2 迭代表达式(2)的参数分岔区间

图7 迭代式(2)当w(2,3)变化时的分岔图 (a)z1分岔图;(b)z2分岔图

图8 w2(2,3)=-0.3,其他参数不变时绘制的吸引子图 (a)吸引子;(b)标准曲面;(c)随机生成的曲面

为了研究多个参数同时变化时迭代式的混沌特性,绘制了二维分岔图.图9是迭代表达式(1)的一个二维分岔图,图10是迭代表达式(3)的一个二维分岔图.

图9 迭代表达式(2)的二维分岔图(w2(2,3)w2(2,1)从0到10,步长0.2,迭代的初始值u=0.5;v=0.3)(a)z1关于w(2,1)w(2,3)的分岔图;(b)z2关于w(2,1)w(2,3)的分岔图;(c)w2(2,3)关于z1,z2的分岔图

图10 迭代表达式(3)的二维分岔图(w2(3,1)w2(3,2)从0到5,步长0.1,迭代的初始值u=0.5;v=0.3)(a)z1关于w(3,1)w(3,2)的分岔图;(b)z2关于w(3,1)w(3,2)的分岔图

图11 迭代表达式(1)的w2(2,3)变化时的Lyapunov指数图,步长0.01;L1是z1的Lyapunov指数,L2是z2的Lyapunov指数

图11是迭代表达式(1)的一个参数变化时的Lyapunov指数曲线图,从该图可以看出其Lyapunov指数为正数的区间.

4 单位区域上双二次有理贝赛尔曲面迭代分析

两个曲面构成一个二维迭代表达式,曲面的形状决定了其是否是混沌的.在第3节中研究的几个曲面都是固定第一个曲面的基本形状,使得其在单位正方形的边界处函数值都是0,中间凸起,最大值为1;第二个曲面是随机生成的.事实上,之所以这种构造方法增大了混沌的概率,是因为第一个曲面的形状与第2个曲面的形状的差异性,在迭代的过程中易于出现混沌.图12所示是迭代式(3)迭代后的函数图像.例如,迭代2次就变成了z1=f(f(u,v),g(u,v))与z2=g(f(u,v),g(u,v)),如此类推,最后出现混沌.

当两个曲面形状相近时,不容易出现混沌状况,图13所示是一个没有出现混沌的迭代.从图13可以看出,随着迭代次数的增加,z1和z2已经逐渐收敛.

图12 迭代表达式(3)多次迭代之后的曲面图形 (a)迭代2次;(b)迭代4次;(c)迭代8次;(d)迭代16次

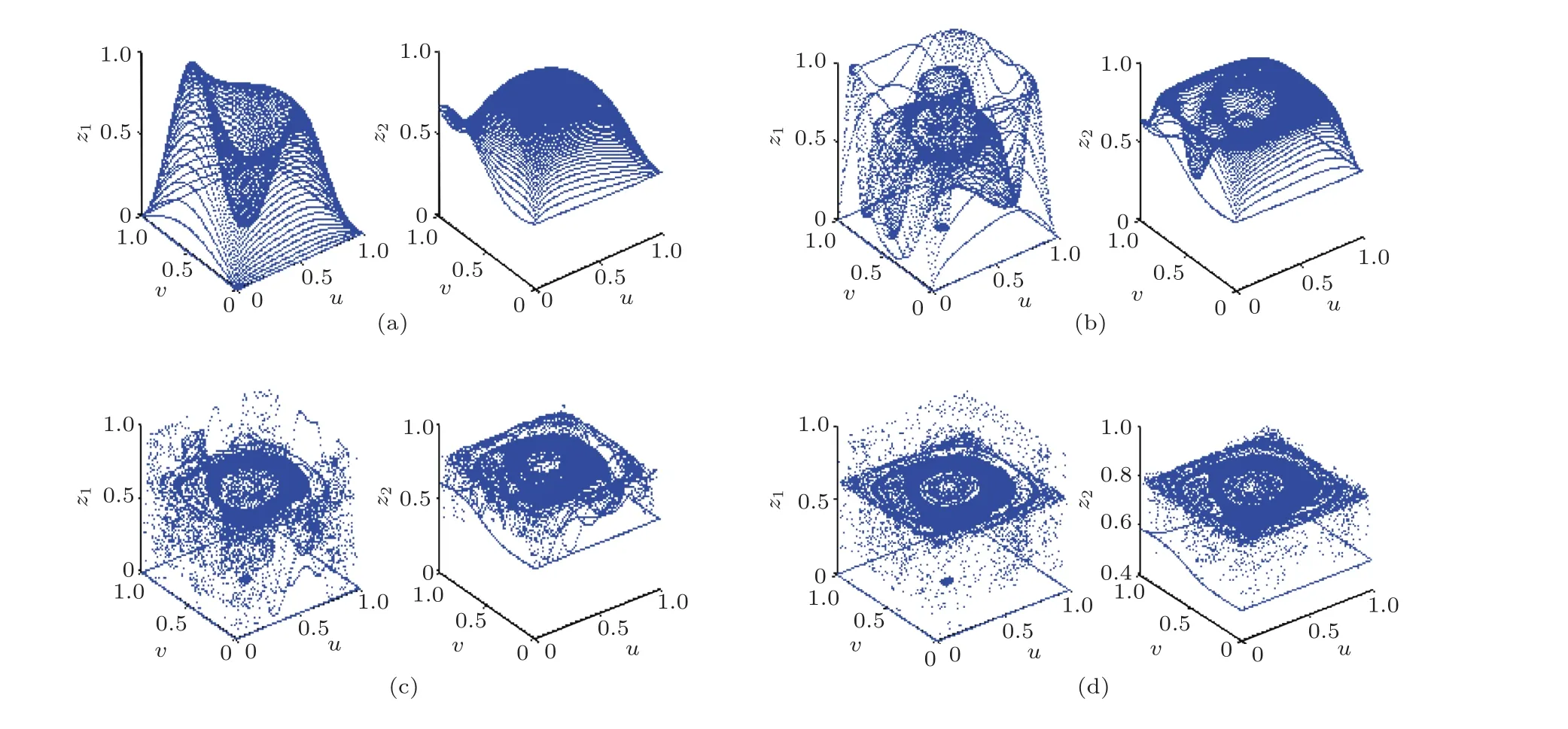
图13 一个收敛的迭代表达式多次迭代之后的曲面图形 (a)迭代2次;(b)迭代4次;(c)迭代8次;(d)迭代16次

从大量的实验结果看,构成迭代表达式的两个曲面形状相近就不易出现混沌,很容易收敛;两个曲面呈现对称或者近似对称,也不会出现混沌;一般当迭代出现混沌时,另外一个非标准函数曲面覆盖区域越大,混沌的区间也越大.

5 图像作为离散曲面的混沌特性研究

图像本质上是一个离散的函数,调整图像,可以构造出混沌映射.基本的构造方法是把图像调整到长宽以及颜色值一样,本文是都调整到1到256,这样就可以让图像的下标与图像的颜色值进行交换,以便实现类似离散动力系统的迭代.

图14中显示了把大小为480×640的两个图像调整为256×256大小,并且把彩色图像也变为灰度图像.

下面以一个简单的迭代为例对图像迭代进行研究.

迭代从x1=23,y1=109开始,图14(b)在(23,109)的灰度值为144,图14(d)在(23,109)的灰度值为255;取出144,255这两个颜色值,然后把(144,255)作为下标,到图14(b)中去查找像素(144,255)位置的灰度值,灰度值为75,再到图14(d)中去查找像素(144,255)位置的灰度值,灰度值为118;然后再以(75,118)为下标,继续迭代取值,如此下去.迭代的序列如下所示:

在12次内还没有重复,也就是还没有陷入到周期点中;编写程序,计算得到该迭代次数小于50000次时,没有出现过第二个(23,109),也就是(23,109)的周期要大于50000.

图14 把图像调整到256×256大小 (a)图像1原;(b)图像1调整后图;(c)图像2原图;(d)图像2调整后

改变初始值进行迭代,计算出当迭代起始点为x1=77,y1=124时,迭代到236次的时候,出现重复,也就是第236次后,其下标也是x1=77,y1=124,所以可以说(77,124)是236阶周期点.进一步实验得到(76,124)也是236阶周期点,但是(75,124)与(78,124)迭代50000次还不曾重复.迭代50000次不重复的点很多,例如,x1=7,y1=12时,迭代72500次也没有出现重复.

下面研究究竟哪些点周期小,哪些点周期大.共迭代25000次,把在25000次迭代之内重复的绘制出来,如图15所示.从图15看,重复的还是少数点.

图15 小于25000的周期点分布示意图

上面研究的是一种最简单的图像迭代,可表示为

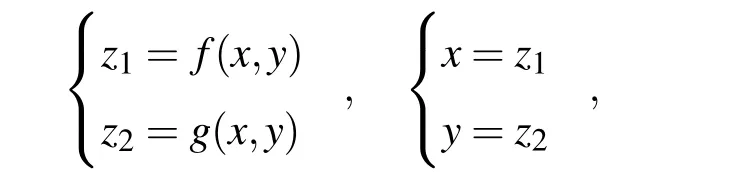
其中 f(x,y)与g(x,y)表示两幅灰度图像.

实验结果还表明,有大量的图像经过这样组对迭代后很容易收敛,得到的基本结论是同一物体的不同图像放在一起进行迭代易于收敛,不同的或者不相近的图像放在一起不易于收敛,所以初步判断改进该方法可以用于图像识别与跟踪、图像理解、图像数据库构造等.

6 总结与展望

本文研究了单位区域内双二次贝赛尔曲面构成的函数的混沌特性,研究发现把其中一个曲面调整为标准曲面,极大地增加了该函数的混沌概率.随机生成两个曲面,构造迭代使混沌的概率不到千分之一,使用本文方法可以使得混沌的概率大于百分之十.在大量的混沌函数中选择三组函数进行了详细研究,通过分岔图以及Lyapunov指数曲线图观察函数的混沌特性.利用这些分岔图可以得到更多的参数,这些参数能够构造出混沌函数.这是一个构造混沌、发现混沌的较好的实用的方法.

进一步的工作需深入研究双二次贝赛尔曲面构成的函数的混沌特性,给出一些结论性的结果,并给出说明或者证明;研究三个三元迭代式在单位区域中的混沌特性,例如把洛伦兹系统族当作一个特例进行研究,研究调整其形状后什么情形下出现混沌;另外,依据现有的混沌理论与实验结果,继续研究图像迭代的混沌特性,期待发现新的结果,例如把一个图像和一个标准函数放到一起迭代,关于这个内容,从最近作者研究结果看,可以作为一种图像识别的方法;事实上,也可以利用单位区域函数的作用研究较规范的湍流问题,如圆柱形管道中的管内的流体的受力、加速度或者速度等可以用标准函数或者亚标准函数来表示,这样可以更好地利用混沌研究湍流问题.

[1]Li T Y,York J A 1975 Am.Math.Monthly 82984

[2]Chen X F,Chen G,Yu X 2000 Chaos Soliton.Fract.10771

[3]Chen Y C 2008 Int.J.Bifurc.Chaos 181825

[4]Liu H,Wang L D,Chu Z Y 2009 Nonlinear Anal.716144

[5]Akhmet M U 2009 Math.Anal.Appl.351804

[6]MengJD,BaoBC,XuQ2011ActaPhys.Sin.60010504(inChinese)[孟继德,包佰成,徐强2011物理学报60010504]

[7]Zhang Y S,Xiao D,Shu Y L,Li J 2013 Signal Process-Image 28292

[8]Liu S X,Guan H Z,Yan H 2012 Acta Phys.Sin.61090506(in Chinese)[刘诗序,关宏志,严海2012物理学报61090506]

[9]Shi Y M,Chen G 2005 Int.J.Bifurc.Chaos 15547

[10]Shu Y L 2008 Nonlinear Anal.691768

[11]Aghababa M P 2012 Chin.Phys.B 21100505

[12]Sun C C,Xu Q C,Sui Y 2013 Chin.Phys.B 22030507