土质路基荷载下地基沉降的修正计算方法

陈伟志，蒋关鲁

（1.西南交通大学土木工程学院，四川 成都 610031；2.高速铁路线路工程教育部重点试验室，四川 成都 610031）

土质路基地基沉降计算是高速铁路设计与施工面临主要难题之一。目前，我国一般采用分层总和法进行地基沉降计算，影响其计算精度主要是应力分析和沉降计算参数的确定。土质路基荷载下应力分析主要是路基基底反力和地基附加应力。传统比例荷载法(γh法，γ为路基土重度，h为路基高度)常作为土质路基基底反力的计算方法，文献［1］、［2］通过离心模型试验和现场填筑试验研究发现，土质路基基底反力受路基宽高比b/h影响显著，提出了路基中心处基底反力修正计算公式。地基附加应力的准确计算在沉降评价中具有关键作用，一般仍将地基土假定为各向同性的弹性体，再基于弹性理论的方法进行分析［3］；文献［4］采用弹性理论和数值模拟结合的手段探讨了路桥交界处地基附加应力的修正计算方法，该法同样适用于普通路基。

地基沉降计算参数主要通过室内试验或现场原位测试确定，近年来，基于原位测试的沉降计算得到广泛应用。文献［5］通过对中等压缩性土一系列原位测试研究，提出了有效的勘探试验方法及合理的指标选择；文献［6］根据载荷试验曲线提出了地基非线性沉降计算的切线模量法；文献［7］将载荷试验与标贯试验成果结合起来提出了地基非线性沉降计算的修正切线模量法。

本文在载荷试验得到的切线模量方程中，引入了考虑路基宽高比修正的地基附加应力，得出了针对土质路基地基沉降计算的修正切线模量法，基于该法分别对胶济客运专线(以下简称“胶济线”)非饱和土地基和海南东环客运专线(以下简称“海东线”)全风化花岗岩地基进行沉降计算验证。

1 土质路基地基沉降的修正计算

1.1 地基附加应力

地基土的力学性质主要表现为明显的非线性、各向异性、不均一性等特征，目前，从考虑地基的非均质非线性角度进行应力分布计算较为困难，一般将地基假定为均质弹性半空间体，再基于弹性理论进行应力求解。Boussinesq于1885年利用弹性理论分析了弹性半无限体表面作用一垂直集中力时内部任一点的应力分布(图1)。其表达式为:

式中:P——集中力；

z——计算点至表面垂直距离；

R——计算点与荷载作用点距离。

式(1)可转换为积分形式:

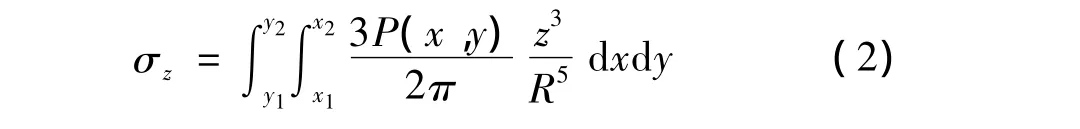
式中，x1、x2和 y1、y2分别为积分限。

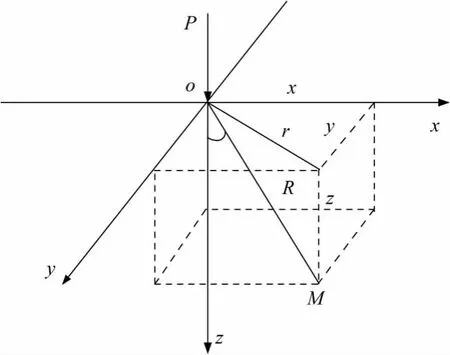
图1 弹性半无限体内部一点应力计算Fig.1 Stress calculation in elastic semi-infinite space

土质路基自重引起的基底应力传统上比较常用的方法是γh法，文献［1］、［2］提出了考虑路基高宽比b/h影响的路基中心处地基反力σc计算公式(修正比例荷载法，即αγh法):

式中:α1，α2，α3——常数，可由相应的地基类型及路基坡度来确定；

b，B——路基顶面、底面宽度；

h，γ，G——路基高度、填土容重、总荷载；

h'，b'——等效荷载高度、宽度。

图2为土质路基基底应力的修正分布，图中实线为按传统比例荷载法得到的路基断面，虚线为按修正比例荷载法得到的修正路基断面。

图2 土质路基基底应力分布Fig.2 Distribution of basal stress of soil subgrade

梯形荷载作用下的地基附加应力，本文仅给出αγh法的计算公式，γh法可由αγh法类似得到。由图2中路基基底应力区Ⅰ、Ⅱ、Ⅲ和公式(2)可推导出土质路基荷载作用下地基中任一点的附加应力［4］:

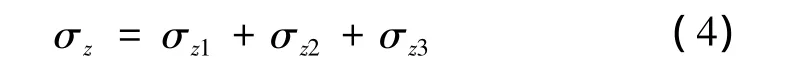
式中:σz1——均布荷载在地基中产生的附加应力，对应图2中的Ⅰ号区域；

σz2——右边三角形荷载产生的附加应力，对应图2中的Ⅱ号区域；

σz3——左边三角形荷载产生的附加应力，对应图2中的Ⅲ号区域。

式中:y0——图2中计算点A在线路纵向上与某一参考点(如桥台背面)之间的水平距离；

x0——图2中计算点A在路基横断面上与线路中心的水平距离。

βi(i=1，2，3，4)可根据式(8)～(11)分别计算:

θi、αi可根据 βi分别由式(12)和(13)求得:

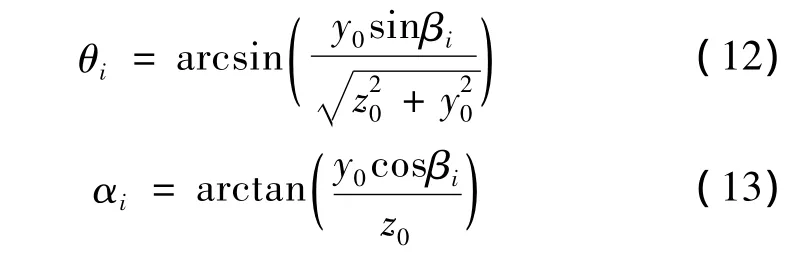
1.2 地基沉降计算

地基中某一分层厚度为Δhi土层在某一附加应力pi作用下，相应的变形模量为Et，则该层土产生的压缩沉降为:

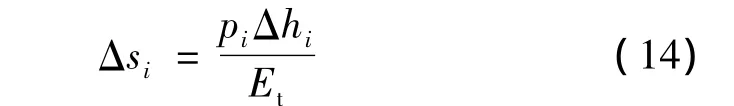
地基总沉降量按分层总和法可表示为:

土体的变形模量受应力水平的影响，文献［6］、［7］将地基假定为非线性非均质弹性体，根据原位载荷试验p-s曲线建立起用附加应力水平表示切线模量的非线性沉降计算方法。

原状土压板载荷试验p-s曲线一般可用双曲线方程表示:

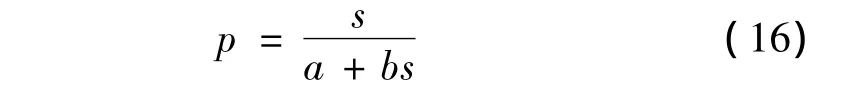
式中，a，b为曲线拟合参数，由式(16)可知，当 s→0时，a=1/Kt，Kt为初始切线基床系数；当s→∞时，b=1/pu，pu为地基的极限承载力。

对式(16)求偏导可得:

压板载荷试验在某一荷载增量Δp作用下，其沉降增量Δs按半无限弹性体的Boussinesq解为:

式中:D——试验压板的直径或边长；

μ——土的泊松比；

ω——刚性承压板的形状系数，圆形承压板取0.79，方形承压板取0.88；

Et——压板底部土体在荷载(p+Δp)作用下对应的非线性切线模量。

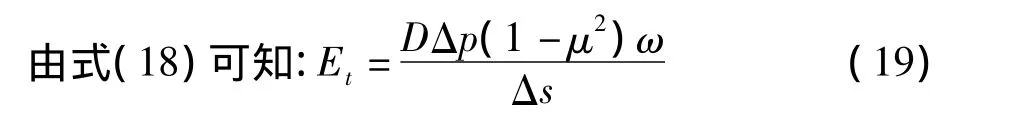
式中，(1－p/pu)2反映了地基中应力水平对土体切线模量的影响，本文称为土体切线模量应力影响系数ζ；E0为土体的初始切线模量:

文献［6］和［7］在式(20)中分别引入了破坏比系数Rf和附加应力修正系数β，对土体切线模量加以修正以求获取准确的沉降计算结果，但Rf是由人为随机选取的，而β值则是根据已有载荷试验资料，假定末级荷载下的计算沉降与载荷试验实测沉降相等的条件下，经拟合计算求得。本文取Rf=1.0，对式(20)中p值则通过考虑路基高宽比(b/h)影响加以修正。

结合式(14)、(15)、(20)和(21)可得:

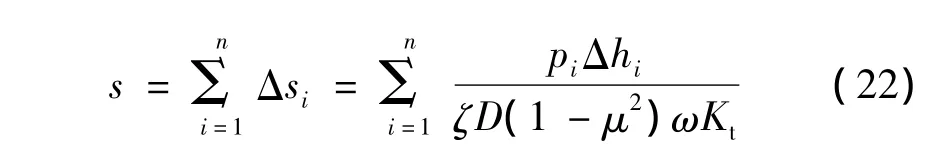
针对土质路基，式(22)中的地基附加应力pi采用γh法计算，本文称为切线模量法，pi采用αγh法计算，本文称为修正切线模量法。

1.3 地基附加应力和切线模量的分布特征

由式(22)可知，地基附加应力pi和切线模量应力影响系数ζ是影响沉降计算的主要因素。本文以路基顶面宽度12.5m、高7.5m、填土重度20kN/m3、路基边坡坡度1:1.5的铁路路基断面为算例，分析了pi和ζ的分布特征，可作为计算精度的评价依据。

1.3.1 地基附加应力

地基附加应力沿深度的分布形态见图3，由图3可知，γh法与αγh法二者得到的地基附加应力分布规律基本相似，均沿深度逐渐衰减(坡脚除外)，同一深度处，γh法计算的pi值并不总大于αγh法，随着距路基中心距离l的增大，出现了相反的情况。在坡脚处，地基附加应力沿深度呈弓形分布，即在一定深度范围内，应力沿深度逐渐增加，表现为应力向地基深层传递的特点，随后曲线出现反弯，应力随深度的增加而衰减。另一方面，浅层地基附加应力受路基高宽比影响显著，随着深度的增加其影响程度减弱。

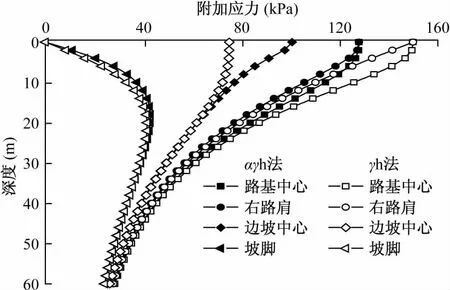
图3 地基附加应力沿深度分布Fig.3 Additional stress distribution along the depth

图4给出了地基附加应力沿路基横向的分布规律。由图4可以看出，地基附加应力沿路基横向均呈Z型衰减分布，即应力随l增大先缓慢递减，再呈线性快速衰减，其衰减幅度随深度的增加而减小，最后曲线趋于稳定。

沉降压缩层厚度的确定，一般根据地基附加应力等于0.1倍或0.2倍自重应力选取，即0.1法或0.2法。图5给出了地基附加应力影响深度的横向分布，由图5可知，按0.1法或0.2法确定的地基压缩层厚度随距l的增大而减小，且γh法和αγh法确定的地基压缩层厚度基本相同。

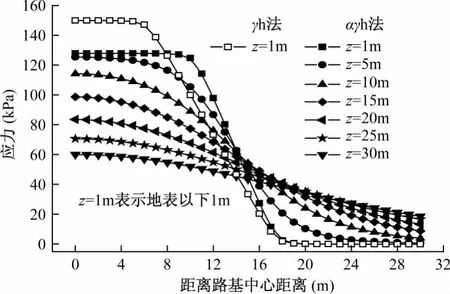
图4 地基附加应力的横向分布Fig.4 Lateral distribution of additional stress

图5 地基附加应力影响深度的横向分布Fig.5 Lateral distribution of additional stress influence depth

1.3.2 切线模量应力影响系数

假定pu=1000kPa，结合图3和图4可给出切线模量应力影响系数沿地基深度和路基横向的分布规律，见图6和图7。从图6和图7可以看出，ζ与pi具有相反的类似分布规律，文中不再赘述。

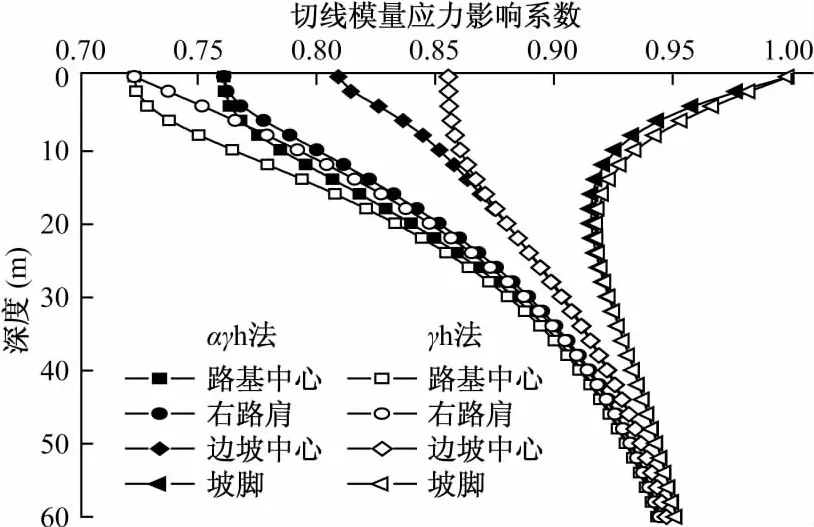
图6 切线模量应力影响系数沿深度分布Fig.6 Distribution along the depth stress influence coefficient of tangent modulus

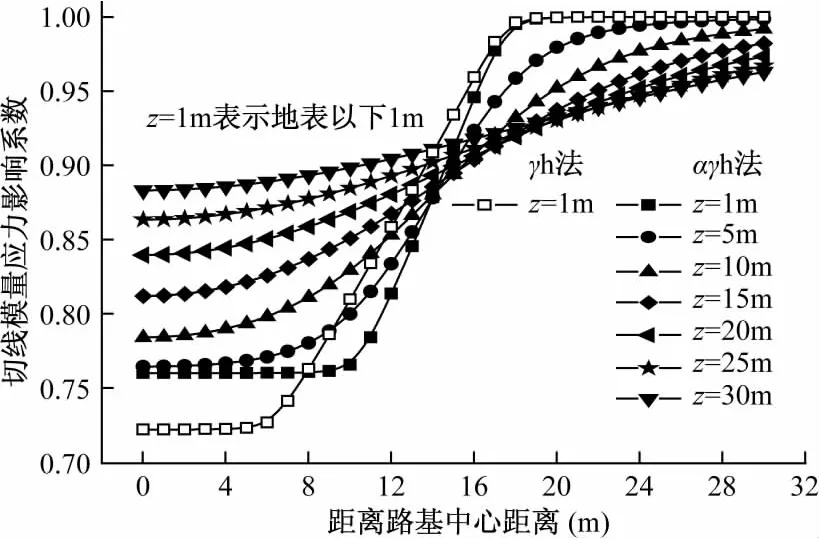
图7 切线模量应力影响系数的横向分布Fig.7 Lateral distribution of stress influence coefficient of tangent modulus

2 现场实例分析

2.1 工程概况

为了验证算法的可靠性，本文选取胶济线和海东线7个路基沉降监测断面(表1)进行计算分析［5］。其中，胶济线试验段位于青州境内，长约12.94km，广泛分布黄土质粉质粘土、粉土、粉质粘土，室内固结试验结果表明［5］，地基土的压缩系数α1～2为 0.117 ～ 0.217MPa－1，属于中等压缩性土，该地区的地下水系不发育，土体饱和度一般在67%～80%之间，地基土又呈现出典型的非饱和性状。海东线试验段在海南省文昌市境内，段内广泛分布全风化花岗岩，其压缩系数为0.141～0.284 MPa－1，亦属于中等压缩性土。

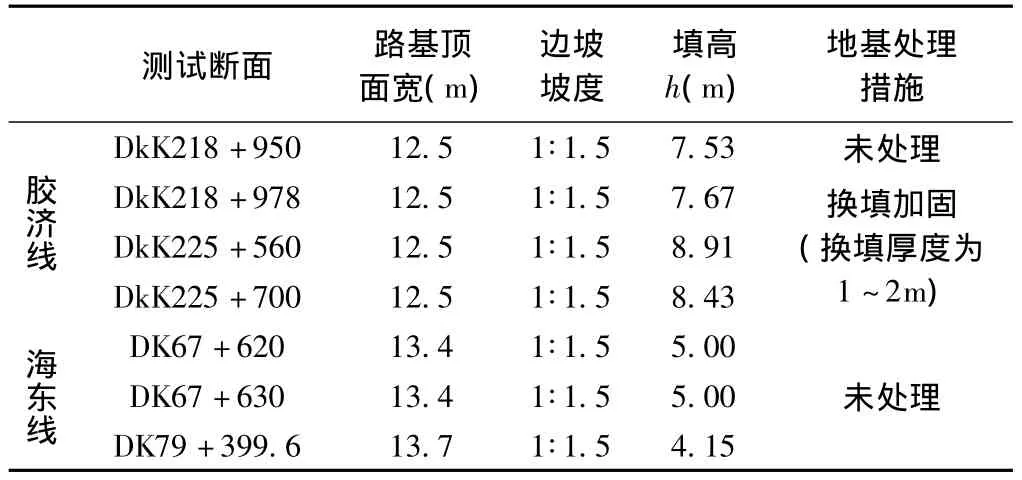
表1 路基沉降监测断面概况Table 1 An overview of subgrade settlement monitoring sections

2.2 计算参数

在胶济线针对天然地基和换填加固地基分别进行压板载荷试验(压板边长为1.1m)；在海东线天然地基也进行了压板载荷试验(压板直径为56.419cm)，试验结果见图8。根据式(16)对图8中载荷试验数据进行双曲线拟合，拟合结果见图8和表2。

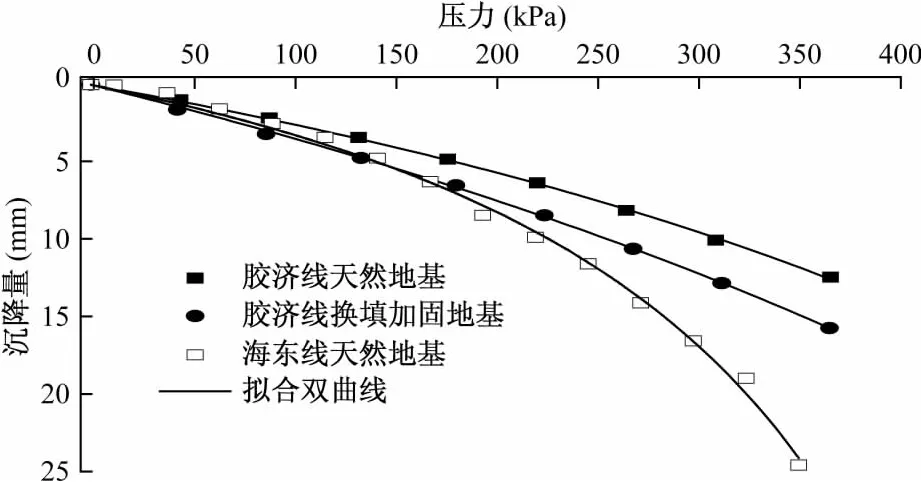
图8 压板载荷试验p-s曲线Fig.8 The in-situ plate loading test curve

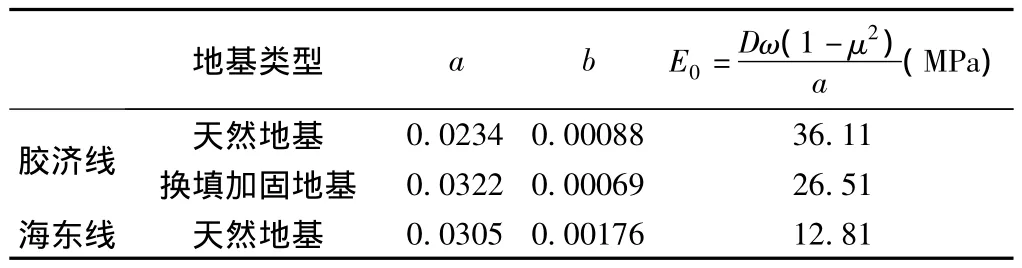
表2 双曲线拟合参数及初始切线模量Table 2 Hyperbola fitting parameters and initial tangent modulus

地基极限承载力pu可由理论计算公式(如Prandtl公式)确定，或根据pu与原位测试指标(包括静力触探指标、标贯试验指标及旁压试验指标等)的经验关系确定。本文计算用的地基极限承载力pu是通过旁压试验确定，其确定方法详见文献［8］，图9为地基极限承载力沿深度的分布情况，由图9可知，pu沿深度分布的离散性大，同一深度处，海东线的地基极限承载力较大。

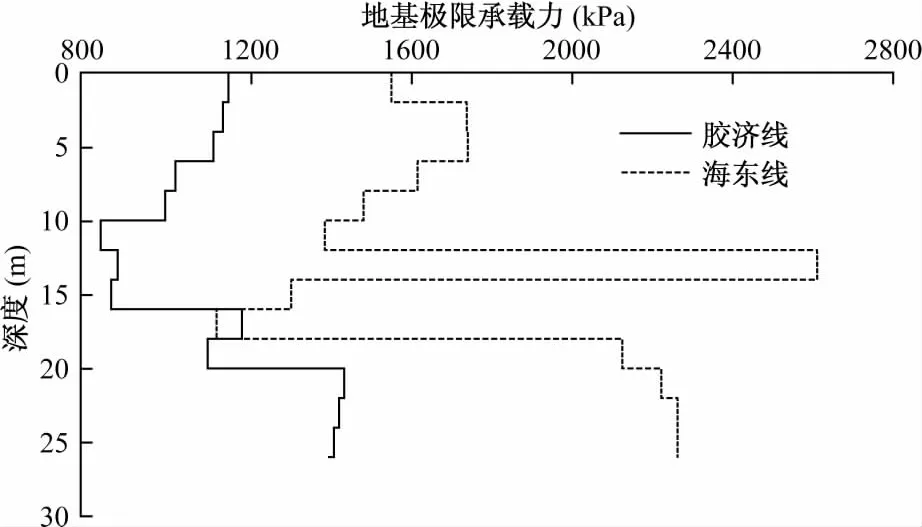
图9 地基极限承载力沿深度分布Fig.9 Ultimate bearing capacity distribution along the depth

2.3 计算结果分析

按γh法和αγh法分别计算表1中各路基断面在路基中心和路肩的地基附加应力，计算时考虑了列车荷载，地基压缩层厚度结合地质条件按0.1法确定，分层厚度取0.5m，根据表2中土体的初始切线模量及式(22)计算地基沉降，其结果见图10(a)。为了分析变形参数对沉降计算的影响，根据室内固结试验和其他几种原位测试试验得到的压缩模量，结合αγh法进行沉降计算，结果见图10(b)。

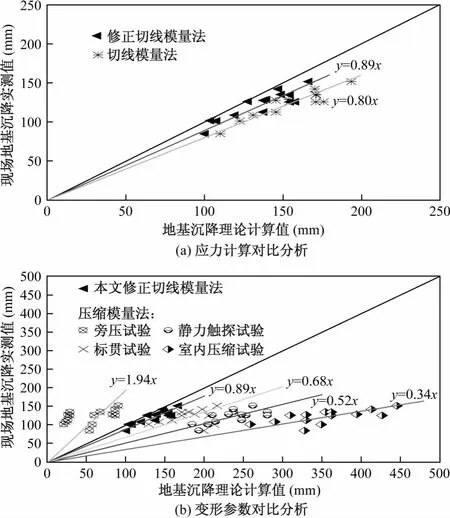
图10 沉降计算结果Fig.10 Result of calculation of settlement

由图10(a)可知，修正切线模量法的沉降值比切线模量法更接近于实测值，其修正系数约为0.89，由图5可知，修正切线模量法与切线模量法按0.1法确定的压缩层厚度基本相同，结合前面的分析可知，地基附加应力和切线模量应力影响系数沿深度的分布特征是造成二者沉降计算结果差异的主要原因，另一方面也说明了采用αγh法进行应力分析比γh法更合理。由图10(b)可知，除旁压试验的沉降值小于实测值外，其余几种算法均大于实测值，以本文修正切线模量法的沉降值最接近实测值，标贯试验次之，室内固结实验的沉降值与实测值相差最大，计算结果表明修正切线模量作为地基沉降计算参数具有可行性。

3 结论

(1)基于压板载荷试验成果，结合考虑路基高宽比(b/h)影响的修正附加应力，用于土质路基地基沉降分析的方法，其计算精度比传统的切线模量法和其他原位测试方法高。

(2)本文修正切线模量根据小面积刚性承压板载荷试验得到，应用于土质路基柔性荷载的地基沉降计算时仍具有一定的准确性和可行性，说明基础尺寸效应和压板刚度在计算沉降时可不予考虑。

(3)地基附加应力分布、切线模量应力影响系数分布及原状土初始切线模量的可靠程度是影响地基沉降计算精度的主要因素，因此，在土质路基地基沉降计算时，考虑路基高宽比(b/h)的影响以期获取更准确的应力分布，及开展深层平板载荷试验以获取非均质土层的初始切线模量都是必要的。

(4)本文方法适用于中低压缩性土地基土质路基的非线性沉降分析，可作为以沉降变形为控制目标的高速铁路地基沉降计算的参考方法，但对于蠕变特性明显的软土地基，其工后沉降大，则需考虑时间因素的影响。

［1］蒋关鲁，王海龙，李安洪.高速铁路路基基底应力计算方法研究［J］.铁道建筑，2009(4):65－69.［JIANG G L，WANG H L，LI A H.Study on the base stresses calculation methods of high-speed railway subgrade［J］.Railway Engineering，2009(4):65 －69.(in Chinese)］

［2］蒋关鲁，王海龙，李安洪，等.土质路基荷载下地基反力试验研究［J］.铁道学报，2012，34(6):69－74.［JIANG G L，WANG H L，LI A H，et al.Experimental study on ground reaction under subgrade［J］.Journal of the China Railway Society，2012，34(6):69 － 74.(in Chinese)］

［3］铁道第三勘察设计院.铁路工程设计技术手册——桥涵地基和基础［M］.北京:中国铁道出版社，2002.［The Third Railway Survey and Design Institute Group Corporation.Technical manual for design of railway engineering:subsoil and foundation of bridge and culvert［M］.Beijing:China Railway Press，2002.(in Chinese)］

［4］蒋关鲁，王力伟，杭红星.路桥交界处地基附加应力修正计算方法［J］.岩土工程学报，2013，35(2):208－218.［JIANG G L，WANG L W，HANG H X.The modified additional stress calculation method of bridge approach foundation under the subgrade load［J］.Chinese Journal of Geotechnical Engineering，201，35(2):208 －218.(in Chinese)］

［5］中铁二院工程集团有限责任公司.客运专线中等压缩性土地基沉降特性及处理技术研究总报告［R］.2010.［China Railway Eryuan Engineering Group Co.CTD. Settlement characteristics and processing technology of passenger medium compression soil general report［R］.2010.(in Chinese)］

［6］杨光华.地基非线性沉降计算的原状土切线模量法［J］.岩土工程学报，2006，28(11):1927 － 1931.［YANG G H.Nonlinear settlement computation of the soil foundation with the undisturbed soil tangent modulus method［J］.Chinese Journal of Geotechnical Engineering，2006，28(11):1927 － 1931(in Chinese)］

［7］李仁平.基于原位试验成果的地基非线性沉降分析［J］.岩土力学，2009，30(2):345 － 351.［LI R P.Analysis of nonlinear settlement of foundations based on in-situ tests［J］.Rock and Soil Mechanics，2009，30(2):345－351(in Chinese)］

［8］TB 10018－2003铁路工程地质原位测试规程［S］.北京:中国铁道出版社，2003.［TB 10018－2003 Code for in－situ measurement of railway engineering geology［S］.Beijing:China Railway Press，2003.(in Chinese)］