基于主成分回归分析的西安房地产价格走势*

洪增林，马卫鹏，余永林

(1.长安大学地球与资源学院，陕西 西安 710054;2.西北工业大学资源与环境信息化工程研究所，陕西 西安 710072)

住房是关系到国计民生的重大问题，目前房价问题已经成为一个引起广泛关注的重要经济问题和社会问题。2012年温家宝总理在十一届全国人大四次会议政府工作报告提出:“进一步落实和完善房地产市场调控政策，坚决遏制部分城市房价过快上涨势头”;“稳定房价和住房保障工作实行省级人民政府负总责，市县人民政府负直接责任。有关部门要加快完善巡查、考评、约谈和问责制度，对稳定房价、推进保障性住房建设工作不力，从而影响社会发展和稳定的地方，要追究责任”。可见中央政府对房地产价格调控的决心和信心不回动摇，并从稳定和抑制房价方面为房地产的健康稳定发展奠定了政策基调。陕西省2012年政府工作报告中明确提出:“支持房地产市场健康平稳发展，多渠道增加住房有效供给，满足自住性、改善性的商品房需求”;“强化各级政府的责任，充分发挥省保障性住房建设公司的作用，继续抓好保障性安居工程建设，加快建设进度，确保工程质量”。陕西省围绕制定一系列的房地产政策其目的也在与保持房价平稳，维护房地产市场的健康发展。在这一大背景下有必要对房地产市场的总体趋势做出判断，对房价问题进行深入分析。为此，笔者以陕西省西安市为研究区域，采用主成分分析法和回归分析法对西安市房地产价格各个影响因素进行了分析并对未来价格走势进行预测。

一、国内文献综述及计量方法

(一)国内文献综述

对国内关于房地产价格的影响因素的文献进行整理发现，目前的研究重点侧重于土地价格［1－2］、货币政策［3］、银行信贷［4］、投资性需求［5］等方面，基于主成分回归方法进行分析预测方面，只有范通达［6］、周振勇［7］、何梓霖［9］等一些学者就其专业领域做出了相应的研究，就基于主成分分析法对房地产价格各影响因素进行降解，然后进行回归分析预测也仅有闫燕［9］、胡磊［10］等进行了相应的研究。回顾文献发现，相应的研究所选指标较少，不能够较为全面地反映影响房地产价格的各个影响因素。为此，笔者参考相关文献，选取11个影响房地产价格的指标，然后进行了定量的主成分回归分析，具有一定的创新性，能够为相关研究提供一些参考。

(二)主成分分析方法

主成分分析是由皮尔逊 (Pearson，1901年)首先引入，后来被霍特林 (Hotelling，1933年)发展，其主要特征在于采取一种数学降维的方法，找出几个综合变量来代替原来众多的变量，使这些综合变量能尽可能地代表原来变量的信息量，而且彼此之间互不相关［11］。

主成分分析的步骤一般如下:(1)原始数据进行标准化处理。(2)计算样本相关系数矩阵。(3)求相关系数矩阵R的特征值 (λ1，λ2…λp)和相应的特征向量 (μ1，μ2…μn)。(4)计算贡献率和累计贡献率。(5)计算主成分得分，并写出主成分表达式 (Z1，Z2…Zn)。

(三)回归方法

在提取主成分的基础上，构建房地产价格的一元和多元线性回归模型，并预测西安市未来几年的房地产市场销售价格。

如果所预测的对象只受一个变量的影响，并且所预测的对象与这个变量之间存在着明显的线性相关关系，那么通常采用一元线性回归预测法，所建立的回归方程，也称为一元线性回归预测模型。如果研究一个被解释变量 (因变量)与两个及两个以上解释变量 (自变量)之间线性关系的，通常采用多元线性回归预测法，其实质上就是一元线性回归的特例［11］。

线性回归的基本步骤如下:(1)确定自变量和因变量;(2)建立回归模型，估计各个参数;(3)统计检验。包括拟合优度检验 (R2检验)、方程总体线性显著性检验 (F检验)和变量的显著性检验 (T检验);(4)利用回归模型进行预测。

二、实证分析

(一)变量选取及数据说明

借鉴相关文献［7－11］，研究选取商品房平均销售价格Y(元/m²)为因变量，选取人均GDP X1(元)、总人口X2(万人)、城镇居民人均可支配收入X3(元)、土地购置费X4(万元)、房屋造价X5(元/平方米)、城乡居民人民币储蓄存款余额X6(万元)、房地产开发投资额占固定资产投资额的比重X7(%)、房屋竣工面积占施工面积的比重X8(%)、房屋销售面积X9(万平方米)、城市居民家庭人均消费支出X10(万平方米)、个人住房公积金贷款利率X11(%)等影响房地产价格的11个指标作为子变量。同时研究通过《中国房地产年鉴》、《中国城市统计年鉴》、《陕西省统计年鉴》、《西安市统计年鉴》、《中国社会经济发展数据库》以及西安人口网中获取因变量和各自变量相关数据 (见表1)。

表1 2000－2011年西安市房地产价格及影响因素数据

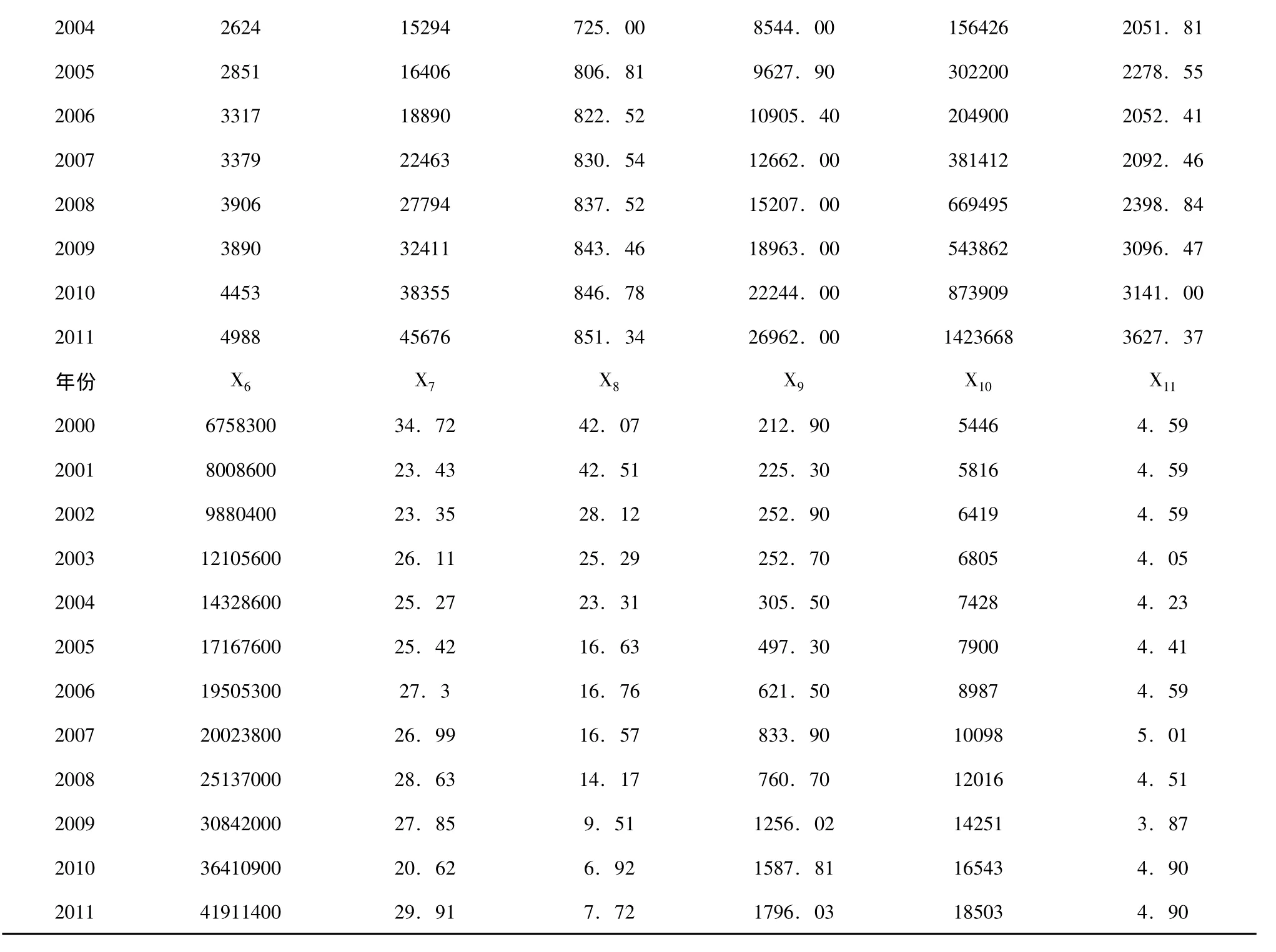
2004 2624 15294 725.00 8544.00 156426 2051.81 2005 2851 16406 806.81 9627.90 302200 2278.55 2006 3317 18890 822.52 10905.40 204900 2052.41 2007 3379 22463 830.54 12662.00 381412 2092.46 2008 3906 27794 837.52 15207.00 669495 2398.84 2009 3890 32411 843.46 18963.00 543862 3096.47 2010 4453 38355 846.78 22244.00 873909 3141.00 2011 4988 45676 851.34 26962.00 1423668 3627.37年份 X6 X7 X8 X9 X10 X11 2000 6758300 34.72 42.07 212.90 5446 4.59 2001 8008600 23.43 42.51 225.30 5816 4.59 2002 9880400 23.35 28.12 252.90 6419 4.59 2003 12105600 26.11 25.29 252.70 6805 4.05 2004 14328600 25.27 23.31 305.50 7428 4.23 2005 17167600 25.42 16.63 497.30 7900 4.41 2006 19505300 27.3 16.76 621.50 8987 4.59 2007 20023800 26.99 16.57 833.90 10098 5.01 2008 25137000 28.63 14.17 760.70 12016 4.51 2009 30842000 27.85 9.51 1256.02 14251 3.87 2010 36410900 20.62 6.92 1587.81 16543 4.90 2011 41911400 29.91 7.72 1796.03 18503 4.90

(二)房地产价格影响因素的主成分分析

1、主成分个数及主成分载荷计算

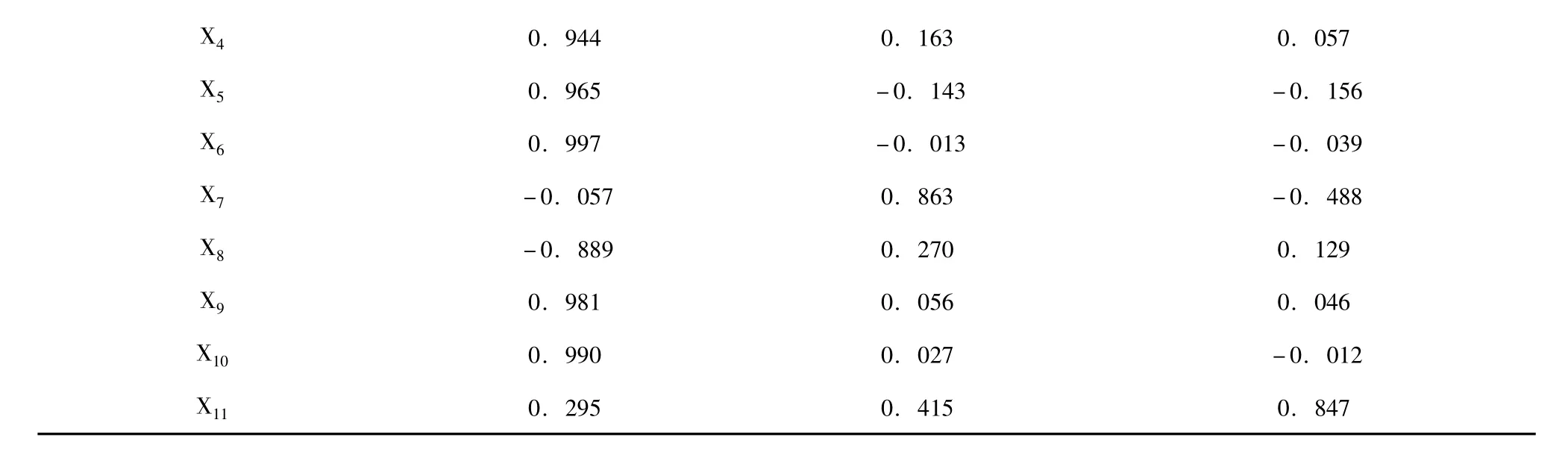
由表2可以看出，特征值λ1=8.383，λ2=1.051，λ3=1.006(其他的特征值小于1，未列出)，前3主成分的累积贡献率为94.914% ＞85%(表2)，为此确定主成分的个数为3，对应的主成分载荷见表3。

由因子得分系数绝对值大于0.5的原则，第一主成分主要由X1、X2、X3、X4、X5、X6、X8、X9、X10支配，反映了人口状况、收入与储蓄水平、房屋成本及房屋销售情况;第二主成分主要由X7支配，反映了房屋开发投资情况;第三主成分主要由X11支配，反映了金融政策。

表2 总方差解释表

表3 主成分载荷

X 4 0.9 4 4 0.1 6 3 0.0 5 7 X 5 0.9 6 5 －0.1 4 3 －0.1 5 6 X 6 0.9 9 7 －0.0 1 3 －0.0 3 9 X 7 －0.0 5 7 0.8 6 3 －0.4 8 8 X 8 －0.8 8 9 0.2 7 0 0.1 2 9 X 9 0.9 8 1 0.0 5 6 0.0 4 6 X 10 0.9 9 0 0.0 2 7 －0.0 1 2 X 1 1 0.2 9 5 0.4 1 5 0.8 4 7

2、主成分特征向量及得分计算

用主成分载荷除以特征值的平方根就得到各个主成分的特征向量 (表4)，并利用主成分的特征向量写出主成分公式Z1、Z2、Z3:

表4 主成分特征向量

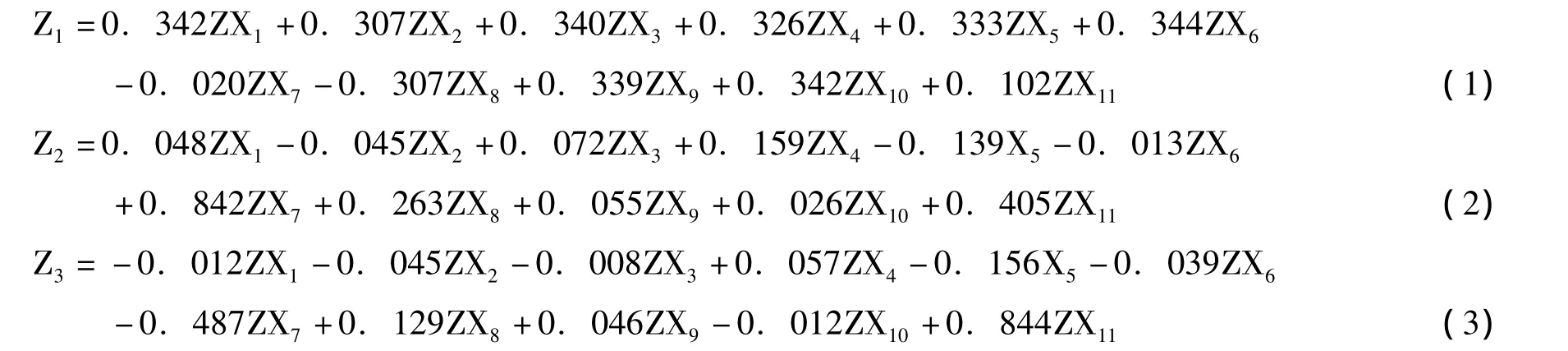
式中，ZX1、ZX2…ZX11为标准化数据。

利用式 (1)、(2)、(3)，计算得到主成分得分 (表5)。

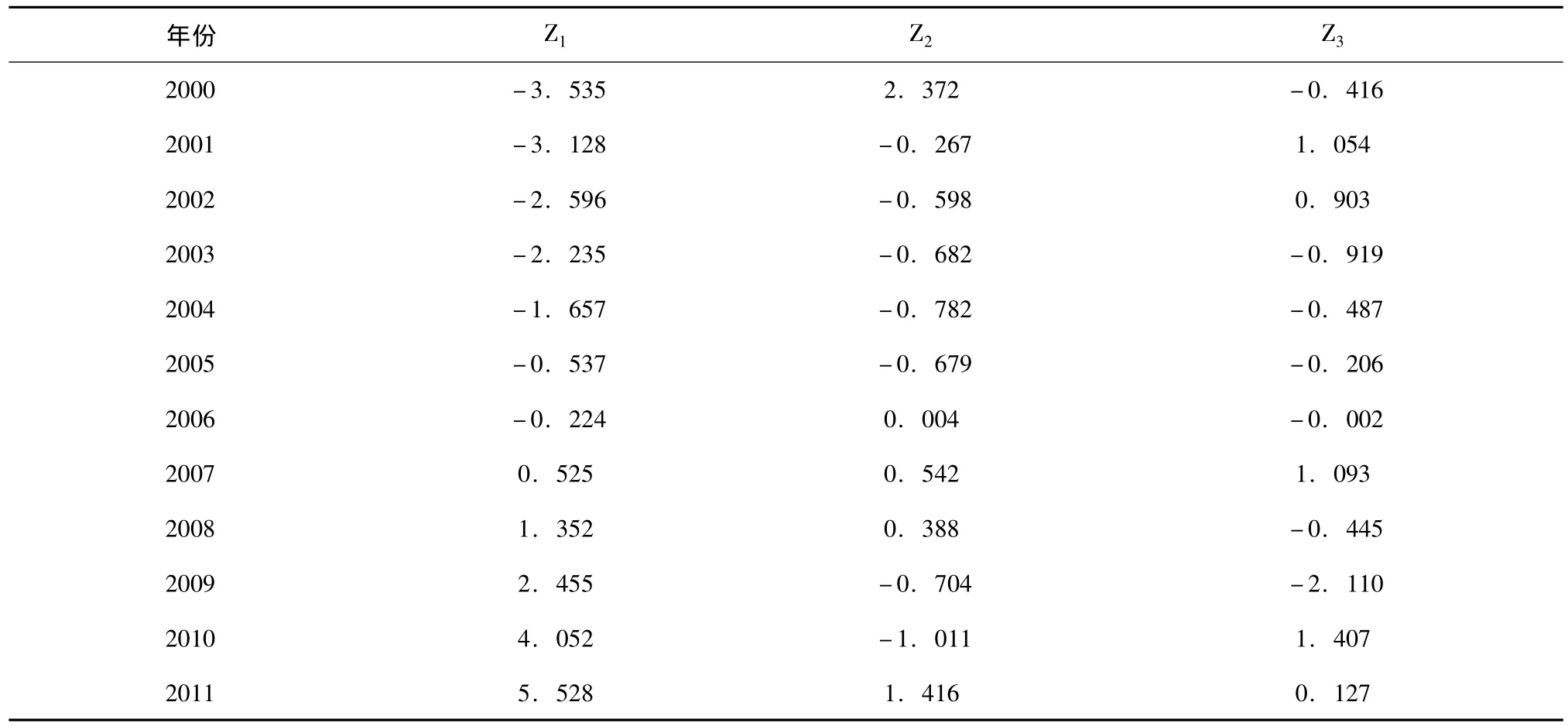
表5 主成分得分计算值

(三)基于多元线性回归分析模型的房地产价格预测

1、房地产价格回归模型建立

在上文主成分分析的基础上，将所提的主成分Z1、Z2、Z3作为自变量，把1900－2010年房地产销售均价作为因变量Y，采用SPSS进行多元线性回模拟，通过拟合发现，初次得到房地产年销售均价的线性回归方程 (3)为:

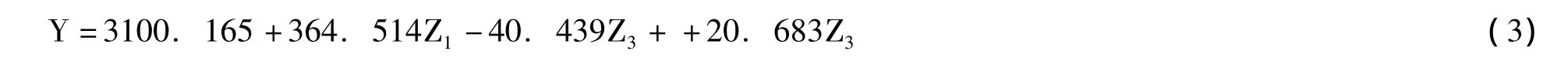
通过拟合发现，模型拟合度R2=0.970，拟合程度较好。通过计算，F检验中Sig.=0.000＜0.05(置信区间)，这说明拟合的回归方程通过了方差检验，方程总体显著。在T检验中Z2的Sig.=0.543＞0.05(置信区间)，Z3的Sig.=0.759＞0.05(置信区间)，这说明Z2、Z3参数的可信度较差，拟合的回归方程未通过T检验，可以将Z2、Z3剔除，然后在进行一次回归模型的拟合。

在剔除Z2、Z3后采用同样的方法对Y和Z1进行拟合，得到房地产价格的回归方程 (4):

采取同样的方法可以发现，模型拟合度R2=0.969，方程的拟合度仍然较好;在F检验中Sig.=0.000＜0.05(置信区间)，这说明拟合的回归方程通过了方差检验，方程总体是显著的;在T检验中Sig.=0.000＜0.05(置信区间)，这说明该参数的可信度较高，拟合的回归方程通过T检验，这表明拟合的一次回归模型成立。

2、Z1、Z2、Z3的方程拟合

由于在建立房地产价格和Z1、Z2、Z3(Z2、Z3已剔除，故不做分析)回归方程时涉及到时间变量(t)，在进行房地产价格回归模型建立后要进行预测必须建立Z1与时间 (t)的预测方程及得到预测值。为此，取2000年=1，2001年=2，…，2011年=12，…，2015年=16，得到时间 (t)的数据，依据表4中Z1数据，采用SPSS软件进行回归拟合。结果表明，模型拟合度R2=0.955，F检验中Sig.=0.000＜0.05(置信区间)，这表明拟合的回归方程通过方差检验，方程总体显著，在T检验中Sig.=0.000＜0.05(置信区间)，这说明该参数的可信度较高，拟合的回归方程通过。为此建立Z1与时间t的回归方程:

利用方程 (5)对Z1进行预测得到2000－2015年预测值，见表6所示。

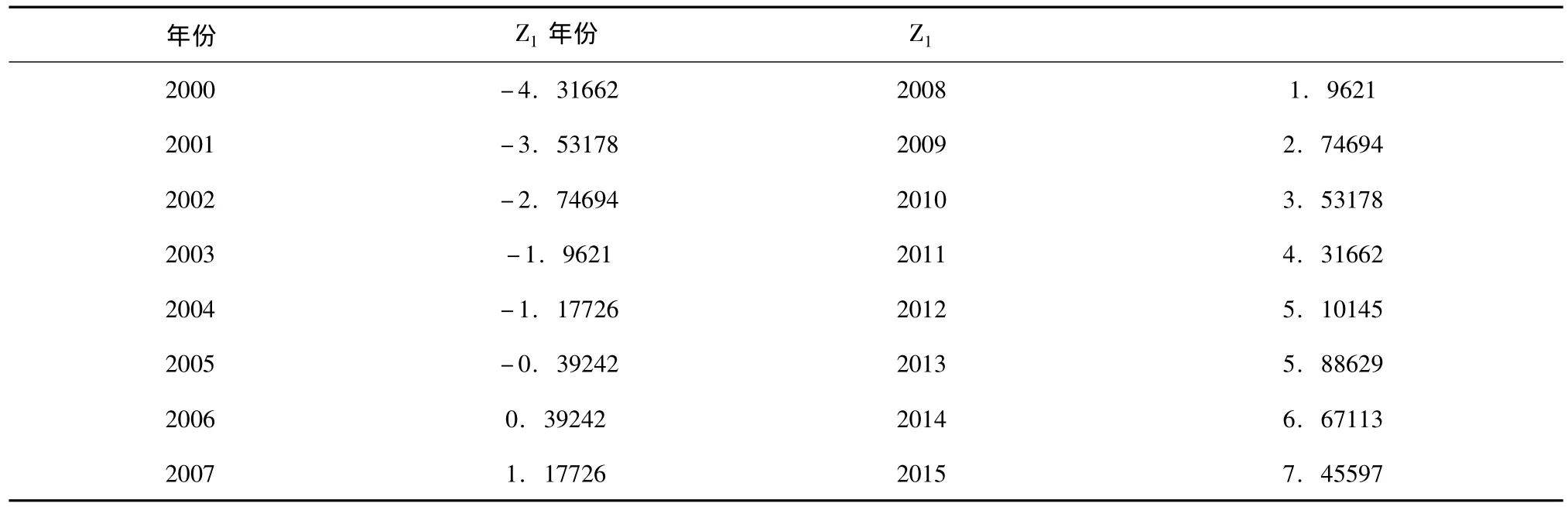
表6 Z1预测值

3、房地产价格预测结果

依据Z1预测得到的2000－2010年数据，带入回归方程 (4)得到西安市2000－2010年房地产价格预测值，并且做预测值与实际值 (平均销售价格)的对比图 (图1)。通过图1可以发现，除了2001、2011年外，其他年份预测值和实际值误差较小，这表明建立的模型精度较高，模型结果具有一定的可信度，可以用来对未来趋势进行预测。为此通过方程以及2012－2015年Z1的数据预测得到2012－2015年西安市商品房平均销售价格为4959.72、5245.80、5531.89和5817.97元/平方米。

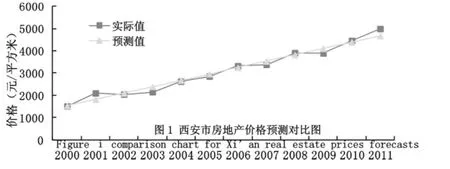
图1 西安市房地产价格预测对比图

三、结论与讨论

研究通过主成分分析得到3个主成分，然后进行回归预测，建立二元回归方程，但由于第二、第三个主成分未通过T检验，被剔除，重新进行回归拟合，结果显示，重新拟合后，拟合度较好，F检验、T检验均通过，回归方程可以用于预测未来房价。通过房价预测结果与房价实际值对比发现，误差较小，这再次说明回归方程成立，同时也可以说明预测模型及结果可为相关研究及政策制定提供参考。由预测结果可以看出，未来几年房地产价格还会上涨。随着关中—天水规划区的进一步实施、沣渭新区的建设、西安国际化大都市战略的逐渐推进以及未来一段时间西安城市化进程的加快，会推动房价的上升，这进一步验证了研究的实证结果。

当然，本文的研究也存在一定的局限性:一是考虑到数据的易得性，指标选取只是选取影响房地产价格的各个可以量化的因素，以便进行预测分析，这些可以量化的数据也是选取对房价有重要影响的指标，对宏观经济运行情况、国内房地产调控政策、国际经济发展状况等不易量化的因素没有考虑在内，这就使得计算结果存在一定的偏差。二是选取各个指标数据来源于统计局以及各个统计网站，各个部门存在统计口径不一致以及统计数据本来就与实际值存在误差的情况，房地产数据是整个西安市的平均价格，从而从致使结果与市场实际值存在一定的偏差。因此，对于西安市房地产格的定量分析预测存在一定局限性，本文模型所选取的因素具有代表性，虽然不能全面反映房地产市场的所有影响因素，对于房地产的预测研究具有一定的现实意义。针对这些存在的问题，笔者将在今后的研究中继续探索和完善。

［1］高波，毛丰付.房价与地价关系的实证检验:1999－2002［J］.产业经济研究，2003，(3):21－23.

［2］姚先国，黄炜华.地价与房价的关系 ［J］.中国土地，2001(9):33－35.

［3］聂学峰，刘传哲.我国货币政策影响房地产市场的实证分析 ［J］.河南金融管理干部学院学报 ［J］.2005.

［4］孔煜.我国银行信贷对房地产价格的影响 ［J］.建筑经济，2008(12):44－46.

［5］张海洋，袁小莉，等.投资性需求对我国房价影响程度的实证分析 ［J］.软科学，2011，5(3):24－30.

［6］范通达，江兵，等.基于主成分分析的多元线性回归用水量模型研究——以安徽省为例 ［J］.基建优化，2007，28(2):53－55.

［7］周振勇，张扬，等.基于主成分逐步回归法的新疆褐牛体重预测模型研究［J］.中国牛业科学，2012，38(1):1－4.

［8］何梓霖，毛德华，等.湖南省长沙县水资源承载力主成分分析研究 ［J］.资源环境与发展，2008(2):17－19.

［9］闫燕.西安市住宅房地产市场预测研究［D］.西安:陕西师范大学硕士学位论文，2011.

［10］胡磊.西安市商品房住宅价格变化研究［D］.西安:西北农林科技大学硕士学位论文，2008.

［11］李子奈，潘文卿.计量经济学 ［M］.高等教育出版社，2010.