考虑风速的风电场等值方法
2013-10-23李洪美万秋兰向昌明
李洪美 ,万秋兰 ,向昌明
(1.东南大学 电气工程学院,江苏 南京 210096;2.徐州师范大学 电气工程及自动化学院,江苏 徐州 221116;3.江苏方天电力技术有限公司,江苏 南京 211102)
0 引言
随着风电的发展,风电在系统容量中所占比例不断增大,风电场对电力系统稳定性的影响也日趋明显。在电力系统仿真模型中考虑风电场对系统的影响显得越来越重要。而目前的风电场通常是由众多机组组成,如果在仿真时考虑各台机组的详细模型会增大仿真计算量,使仿真时间大幅增加。所以建立风电场的等值简化模型成为进行电力系统仿真必须面临的问题。
双馈风电机组(DFIG)由于具有有功功率和无功功率解耦控制的特性,成为目前风电场中应用最为广泛的风电机组。目前国内外很多文献对含有该机组的风电场的等值问题进行了探讨[1-10]。很多等值模型为了简化等值过程,多是假设风电场所有风电机组风速相同来进行等值处理的。由于风电场规模一般较大,各台机组风速不同,所以有文献取风电场的平均风速作为等值机组的输入风速,但风电机组的功率输出与其输入风速并非线性关系,所以该等值方法误差较大。为了减小等值误差,文献[11-13]利用风电机组风速功率关系,计算出每台机组在各自风速下的有功输出,然后将输出功率叠加,倒推风速。该方法计算结果相对较准确,但计算量大。
文献[14]根据风轮机机械特性曲线,将风电机组按照转子转速分为3组,然后进行等值。但该等值方法的前提是要计算出各台机组的转子转速,从而增加了分类的计算量。
本文根据风电机组输入风速与输出功率的关系,在分析影响输出功率的各个因素的基础上,提出了考虑风电机组的风能利用系数而进行风速等值的新方法。
1 风电场风速等值
忽略风电机组损耗,根据风力发电原理,风电机组输出功率为:
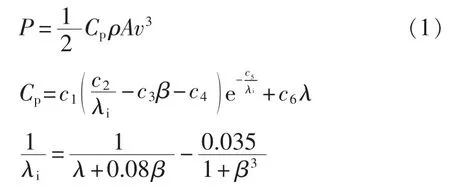
其中,λ=ωrR/v为叶尖速比,R为叶片的扫风半径,ωr为风轮机转速;P、Cp、v分别为机组的输出功率、风能利用系数和机组轮毂高度处风速,最大风能利用系数Cpmax=0.48;ρ为空气密度;A为风电机组叶轮扫风面积;β为风轮机叶片桨距角;c1=0.517 6,c2=116,c3=0.4,c4=5.0,c5=21.0,c6=0.006 8[15]。
风电场总的输出功率为(假设各机组型号相同):
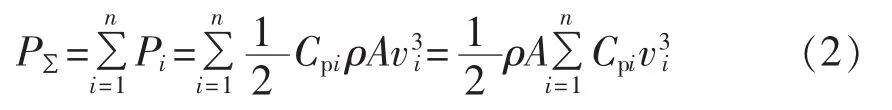
其中,n为机群机组总数。
由等值前后风电机组总的额定功率不变,设机组i的额定功率为Pie,由于同一风电场一般采用额定功率相同的机组,所以有Pie=Pe,Pe为机组的额定功率,即:
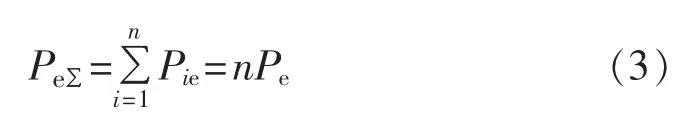
所以,有:
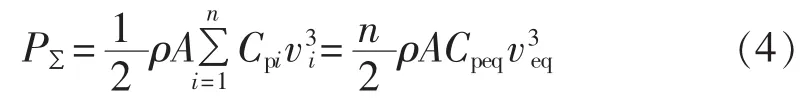
其中,veq为风电场等值风速,Cpeq为等值风能利用系数。
则可得:
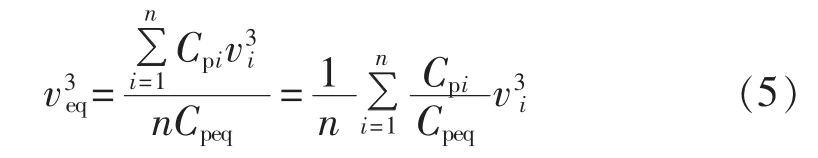
由式(1)知,当风速小于等于额定风速时,β=0,此时Cp只与叶尖速比λ有关,λ是转速与风速的比值。而风电机组转子转速是风速的分段线性函数[16],具体关系如图1所示,图中转子转速ωr为标幺值。
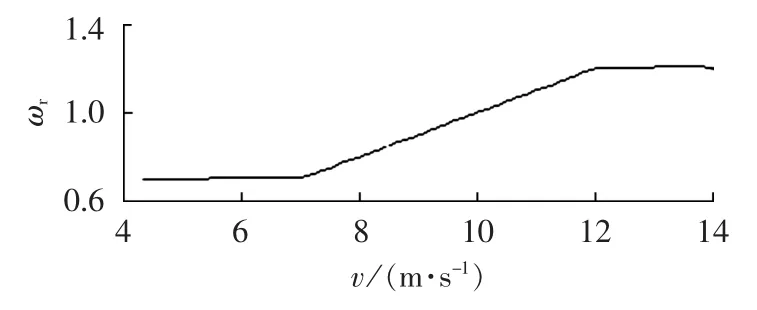
图1 风速-转子转速曲线Fig.1 Curve of wind speed vs.rotor speed
这里针对额定风速为13 m/s的某一具体风电机组,根据其实际的风速-转矩数据,通过曲线拟合得到其风速-转速数学表达关系见式(6)。所用风电机组参数如下:发电机,额定功率为1.632 MW,额定电压为 690 V,额定频率为 50 Hz,Rs=0.00706 p.u.,Rr=0.005 p.u.,Xm=2.9 p.u.,Xs=0.171 p.u.,Xr=0.156 p.u.,H=5.04 s;电缆,R=0.1153 Ω/km,L=0.00105 H/km,C=11.33 μF/km。

可以看出,风速大于7 m/s小于等于13 m/s时,λ近似为常数,即在该段风速范围内机组运行于最佳叶尖速比,此时各台机组的风速虽然不同,但Cp值相同,为简化等值,取Cpeq为该风速段的值,即Cpi=Cpeq(7<vi≤13),由式(5)知,该风速段机组的等值风速为:

当风速高于额定风速或低于7m/s时,Cpi≠Cpeq,此时根据关系式(5)只要求得Cpi/Cpeq=αi比值即可。
通过实际仿真数据得到4.5<v<7和12.5<v≤16时其风能利用系数比值关系表达式分别为以及 αi=当风速大于16 m/s后,机组输出功率恒定。
对上述关系进行综合得到等值风速表达式:

2 风电机组参数等值
本节主要研究参数相同的机组等值问题,所以等值前后机组参数只有个别发生改变,发生变化的参数等值如下:
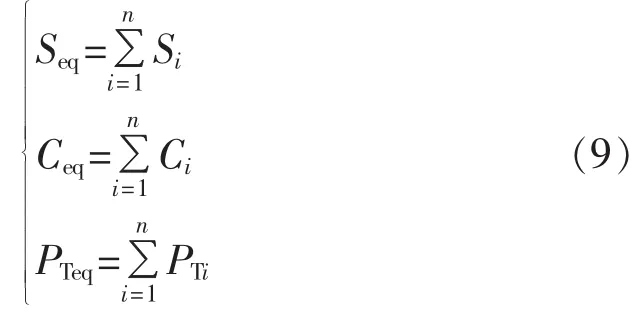
其中,S为风机的额定输出功率;C为逆变器电容器电容;PT为风轮机的机械功率;下标eq表示等值参数。
3 仿真验证
以某风电场为例进行了仿真验证。该风电场35 kV线路共2回线,线路总长20.523 km。一回主干线:LGJ-240/40型线路长度为 9.331 km,LGJ-95/20型线路长度为1.503 km,共有13台风机。二回主干线:LGJ-240/40型线路长度为 9.331 km,LGJ-95/20型线路长度为0.358 km,共有14台风机。风电机组采用恒功率因数控制。取风电场一天24 h运行情况,风速、有功功率取样间隔5 min。
风速分别采用如下2种等值方式进行等值。
a.等值方式1,采用式(8)进行等值。
b.等值方式2,采用下式进行等值:
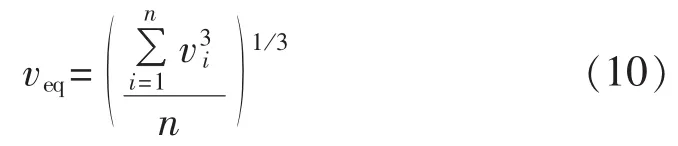
采用上述2种方式得到的等值风速如图2所示。将上述2种等值方式得到的风速代入等值系统与原系统的实测数据进行比较,图3为风电场接入点有功功率输出P比较曲线,图中P为标幺值。

图2 风电场等值风速Fig.2 Equivalent wind speed of wind farm

图3 风电场接入点有功功率Fig.3 Active power of PCC
从仿真图可以看出,采用本文所述的等值方式1,风速波动时,系统的有功功率更接近于实际系统。而采用等值方式2会产生较大的等值误差。
从上述2种情况下的仿真比较可以看出,为了减少风电场等值误差,在求取风电场等值风速时,应该考虑机组在不同风速下的风能利用系数的不同,而不是简单地采用等值方式2所述的方法将所有风况下机组都看作运行于最佳叶尖速比来进行等值,这样势必会导致等值不准确,特别是在大风速时会产生较大的等值误差。
4 结论
本文研究分析了风速与风机总输出有功功率之间的关系,提出风电场等值风电机组新的风速等值方法,该方法考虑了风电机组在不同风速情况下风能利用系数不同的特点,在求等值风速时,不仅考虑机组风速,还考虑了机组的风能利用系数,分别求得低风速段、中风速段和高风速段的风能利用系数与最佳叶尖速比时的风能利用系数的比值,采用风速的立方分别乘以风能利用系数比值,然后叠加取平均值,得到等值风速的立方值,从而求得等值风速。通过仿真,证明了该等值方法较常规等值方法误差更小。本文研究为相同类型机组等值提供了一种简洁有效的等值途径。
