风电接入对继电保护的影响(一)
——鼠笼式风电场电磁暂态等值建模
2013-10-23张保会李光辉郝治国郭丹阳王小立
张保会 ,李光辉 ,王 进 ,郝治国 ,郭丹阳 ,王小立 ,2
(1.西安交通大学 电气工程学院,陕西 西安 710049;2.宁夏电力公司调度中心,宁夏 银川 750001)
0 引言
我国西北部局部地区风能资源蕴藏量丰富,但远离东部负荷中心,因此采用大规模、高集中、远距离风能开发模式。由于风电场包含的机组数目多,仿真其快速动态的电磁暂态过程需要的时域数值积分运算量相当巨大,因此在计算多个大型风电场的详细电磁暂态数值仿真模型上遇到了前所未有的难题:其一,风电场数量多,且场内风机台数巨大,建立这种仿真模型较为繁琐;其二,若电力系统所含风电场数目巨大,采用离线PSCAD/EMTDC对其电磁暂态过程进行仿真耗时长,几乎无法完成。
对于鼠笼式定速感应发电机(FSIG)风电场等值问题,文献[1-2]建立了用单台风机表征的适用于计算稳态潮流的风电场等值模型。文献[3-4]综合考虑传统轴系模型,采用故障结束后FSIG风机的转速作为机组分群的指标,建立机电暂态多机等值方案。目前,对风电场等值模型的研究仍停留在用于潮流计算的稳态模型与用于系统暂态稳定性分析的机电暂态模型[5-7]。大规模风力发电的投入同样对依据电压、电流波形特征的继电保护和控制装置的动作行为带来了不可忽视的影响[8-10],分析这种影响的基础是电磁暂态过程的数值仿真,而仅考虑潮流计算与机电暂态等因素的等值模型难以满足电磁暂态过程研究的需要,必须在全面考察变风机、风电场的故障特征的基础上,才能提出有效的电磁暂态等值策略与实现方案。
本文阐述了FSIG风电场电磁暂态等值的目标,提出FSIG风电场多机电磁暂态等值方法,克服了传统单机等值模型精度不足的问题。以故障初始时刻的标幺值功率作为FSIG风机分群的指标,采用K-means算法来实现机组的分群过程。利用基于机组容量加权的参数聚合的方法计算等值风电机组参数。在PSCAD/EMTDC软件平台上验证了等值方案的有效性。
1 FSIG风机的分群方法
众所周知,电力系统中的等值计算不可能是完全等效的,按照所关注的研究对象,可以采用不同的等值方法。本文所研究的内容属于风电场电磁暂态等值,主要用于研究大规模风电场并网对系统继电保护的影响,因此不仅要求稳态和故障时等值模型与详细模型输出的功率一致,同时还要求等值前后具有一致的电压、电流信息。电磁暂态过程持续时间短,关注的是影响继电保护动作时间窗内秒级的故障电气量信息。
文献[11-12]中指出,当机端正常工作电压为us=Umej(t+φ)时,FSIG 的 A 相故障电流的表达式如下:

其中,isA为A相故障电流;UD为机端电压跌落幅度;Um为机端正常电压幅值;φ为机端电压初始相位角;X′s为瞬态电抗;Xs为稳态电抗;τ′r为转子电路瞬态时间常数;s′为机组滑差;ωr为机组当前转速;τ′s为定子电路瞬态时间常数;Xs(s)=Xs(1+sτ′r)/(1+sτr),τr为转子电路时间常数。
在求取式(1)中故障电流3个分量的幅值时,假设转子电阻Rr=0和滑差s′=0,有:

由式(1)和式(2)可知,FSIG 的故障电流不仅与故障电压跌落水平、风机自身的参数有关,同时与风机当前的瞬时转速也有着紧密的联系。因此必须将具有相似电磁暂态信息的风机分到同一机群后,进行多机等值以提高等值精度。而由于FSIG机组稳态均运行在同步转速附近,由于测量等一系列误差因素的存在,依靠测量机组故障前的转速进行分群是不现实的,因此必须将转速转换为其他量。忽略阻尼,FSIG转子运动方程为:
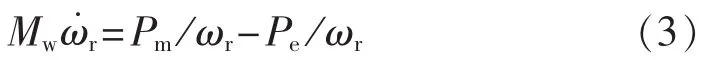
其中,Mw为FSIG转动惯量;ωr为FSIG转子转速;Pm为机械功率;Pe为电磁功率。稳态运行时,式(3)等于0。
由于风能在地域上的分布不均,同属于一个大型风电场同型号的风机所捕获的风能也存在巨大的差异。由式(3)可知,当外部发生故障时,电机转速增量取决于输入的机械功率与输出的电磁功率之差,而短时内风机输出的机械功率基本不变。因此,本文采用风机故障前机械功率差来反映机群的相同程度,当这个最大值小于某个给定的门槛值ε时,则可以将其归于同一机群,此时划分等值机群的指标如式(4)所示。

风电场控制中心能实时监测风电场内部所有风机输出的功率,可以将故障前某一时刻所有风机的有功功率提取出来,然后经过一定的算法,将风机分成数个机群。减小门槛值ε的值可以提高等值的精度,但同时增加等值机群的个数。
本文采用K-means算法[13]实现FSIG风电场机组分群过程。该算法是以准则函数E收敛后得到的值最小为分类标准,达到将N个数据样本分成K个类的目的,并使其中每个类中的所有样本具有比较高的相似程度,而类与类之间数据样本相似程度比较低。
使用K-means算法对FSIG风电场机组分群的计算步骤简述如下。
a.从风电场控制中心提取全部FSIG风机的N个输出功率数据样本,估计需要分成的机群数目K,并以任意K个机组的输出功率样本作为初始聚类中心。
b.分别计算各个FSIG风机的输出功率与各聚类中心的距离,并将其分别归类到距离其最近的聚类中心所在机群中。
c.计算当前每个机群的FSIG风机的输出功率平均值ai与准则函数E:

其中,ai为第i个机群中FSIG风机输出功率的平均值;gi为第i个机群中所有FSIG风机的输出功率集合;ξ为gi中的输出功率样本;Ni为第i个机群中机组的总数;E为准则函数。
d.用ai替代原来的聚类中心,执行步骤b—d直到E收敛。
e.若计算出来的任意一个机群内机组的输出功率不满足式(4),则增大机群数目K,重复执行步骤b—d。
2 FSIG风机参数聚合
FSIG分群后,需要按类进行详细模型参数聚合。传统的发电机参数聚合一般在频域内进行,并假设发电机及其控制环节频域参数聚合可以分解成若干个部分分别进行聚合。首先通过一定算法计算出机群某环节集合函数G(s),并选择等值机包含待定参数的相应环节模型H(s),然后使用优化算法使H(s)与G(s)频域特性最接近,选择适当的激励,频率扫描范围一般取0~10 Hz,求取式(6)所示函数的最小值,可计算出 H(s)中等值机的参数[14]。
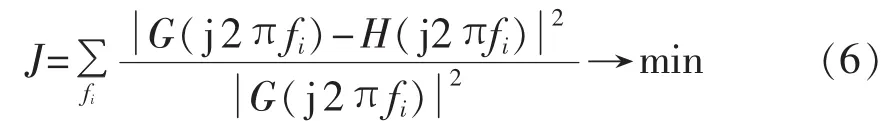
频域聚合法在理论上是非常严谨的,且其物理透明度大,计算出的模型能直接用于机电或者电磁暂态分析。但是其聚合的算法比较复杂,当需要聚合的系统较大、发电机较多时,需要很长的计算时间。本文采用基于机组容量加权的参数聚合法计算FSIG等值风机的参数,简化了计算过程,优化了计算时间,可应用于工程实际中[15]。
将同一个等值机群等值为1台FSIG风电机组,在进行参数聚合时假定如下:
a.被等值的FSIG机群接在同一条等值母线上;
b.FSIG等值机输入的机械功率及电磁功率与被等值的FSIG风机详细模型中各值之和相等;
c.同一等值机群中FSIG风机具有相同的转速。
FSIG机群详细的模型参数聚合问题可以分成以下3个环节进行:FSIG电机转子运动方程参数、FSIG阻抗参数和箱式变压器参数。
分别对上述3个环节进行参数聚合就能得到FSIG风机群的等值模型。假设按照基于功率分群的原则,通过K-means算法得到待等值的某群风机M={1,2,3,…,m},其额定容量 S={S1,S2,…,Sm}。 则等值FSIG风机的容量为这m台风机的容量之和,同时,按照假设条件,等值机输入的机械功率及其电磁功率与详细模型中各值之和相等,则有:

其中,S为风机的容量;Pe为风机的电磁功率;Pm为风机输入的机械功率;下标e代表等值FSIG风机;下标i为FSIG风机编号。
2.1 转子运动方程参数聚合
在待等值的风机群M中,假设第i台FSIG风机转子运动方程为:
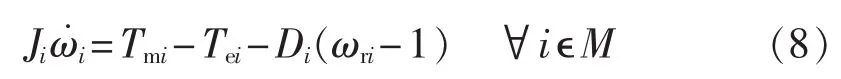
其中,J为风机转子转动惯量;ωr为风机转子转速;Tm为风机输入的机械转矩;Te为风机的电磁转矩;D为阻尼系数;下标i为FSIG风机编号。
式(8)中各值均为以自身额定容量Si为基值的标幺值。为得到等值FSIG风机的转子运动方程,需转换到以Se为基值的标幺值系统,则式(8)可以化为:

根据前述待等值的机群中所有机组转速一致的假设条件,并设所有机组的转速均为ω,将待等值的机群中的m台风机的转子运动方程相加得到:
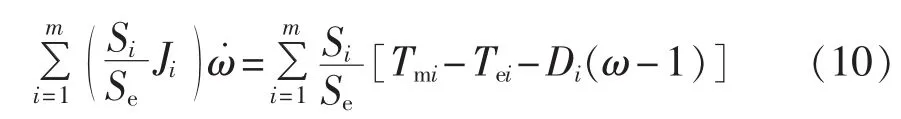
设经参数聚合得到的等值FSIG风机与详细模型中风机的转子运动方程具有相同的表达形式,以Se为基值的方程为:
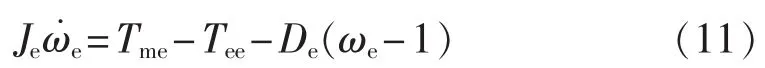
比较式(10)和式(11)可以得到等值FSIG风电机组的相关参数。
转子转动惯量:

阻尼系数:
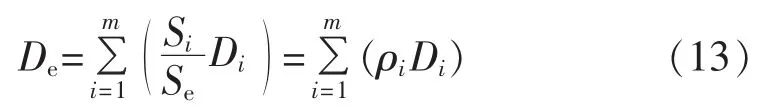
其中,ρi为编号i的FSIG的导纳参数在等值机中所占比重。
可见,聚合后得到的等值FSIG风电机组的转子转动惯量、阻尼系数在等值机组标幺值系统下,是以Si与Se的比值为权重的加权平均值。值得注意的是,电磁转矩和机械转矩在详细模型与等值模型中,其有名值并没有发生变化。当m台机组型号一致时,等值前后转子转动惯量与阻尼系数在各自容量下的标幺值不变。
2.2 等值电机阻抗参数聚合
假设待等值的m台FSIG风机都并联在同一母线上,所有机组采用T型等效电路,将m台机组的T型等效电路并联,然后简化成1台机组的等效电路,以此来求得等效模型中的参数,如图1所示。
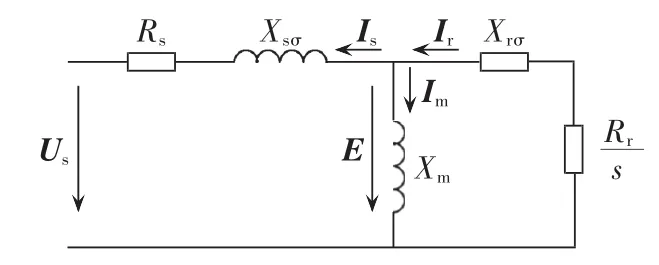
图1 FSIG的T型等效电路Fig.1 T-type equivalent circuit of FSIG
采用基于容量加权的聚合算法计算FSIG等值风机阻抗参数,其求解方程如下:

其中,Xse、Xre、Rse、Rre、Xme分别为等值 FSIG 风机以额定容量Se为基值的定子、转子的电抗和电阻,以及等效互抗的标幺值;Xsi、Xri、Rsi、Rri、Xmi分别为第 i台FSIG风机以各自额定容量Si为基值的定子、转子的电抗和电阻,以及等效互抗的标幺值;si、se为第i台FSIG风机以及等值机的相对滑差。
假设所有FSIG风电机组的相对滑差s=1(转子堵转状态),可求得等值FSIG机组的相关聚合阻抗参数:
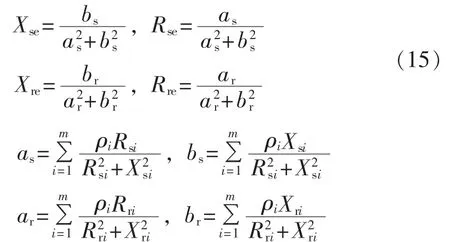
等效互抗:

特别地,当m台机组型号一致时,等值前后上述FSIG的阻抗参数以各自容量为基值的标幺值不变。
2.3 箱式变压器参数聚合
箱式变压器中待聚合的参数包括容量以及阻抗值。按照前面的等值思想,等值变压器容量取详细模型中所有箱式变压器容量之和:

其中,STi为第i台变压器的容量;STe为等值变压器的容量。
在PSCAD/EMTDC软件平台上变压器统一采用如图2所示的Γ型简化等效电路。
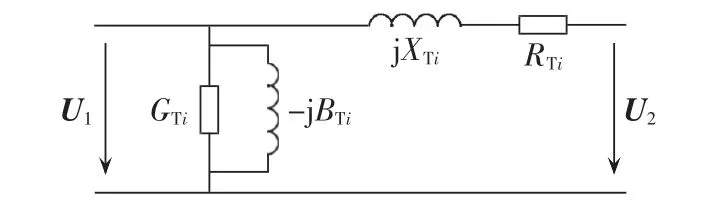
图2 变压器Γ型简化等效电路图Fig.2 Γ-type equivalent circuit of transformer
图中 GTi、BTi、XTi和 RTi分别为第 i台变压器电导、电纳、高低压绕组的总电抗和高低压绕组的总电阻,均为以自身容量为基值的标幺值。等值变压器的参数求取方法类似于FSIG等值电机阻抗参数求取方法,在此不再赘述。
特别地,当m台变压器的型号一致时,等值前后变压器的阻抗参数以各自容量为基值的标幺值不变。
3 等值方案验证
本文仅在PSCAD/EMTDC中建立包含10台FSIG风电机组的小型风电场模型,其结构图如图3所示。为简化起见,本文暂不考虑风电场内部的电缆及架空线路的阻抗。
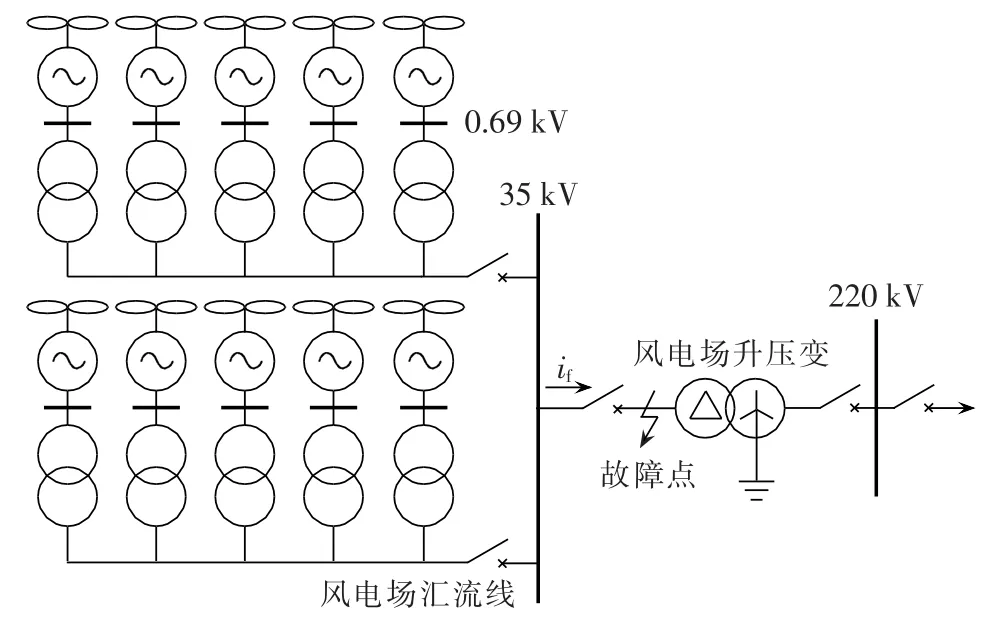
图3 风电场布局Fig.3 Layout of wind farm
通常同一风电场内部FSIG风机的型号相同,少数情况下,也有可能包含2~3种型号。本文在此做2种情况考虑:一是风电场内10台FSIG风机型号相同;二是风电场内10台FSIG风机分2种型号,每种各5台。
3.1 风机型号相同
假设风电场内10台FSIG风机的型号相同,具体的参数值如下:Se=1.6 MV·A,Pe=1.5 MW,fe=50 Hz,Ue=0.69 kV,Xm=3.342 p.u.,Rs=0.0102 p.u.,Xsσ=0.1513 p.u.,Rr=0.0083 p.u.,Xrσ=0.1546 p.u.,J=1.5p.u.。风机箱式变压器及风电场出口升压变参数为:风机箱式变压器,Se=1.6 MV·A,Xt=6%p.u.,Rt=1%p.u.,Gt=1%p.u.;风电场升压变压器,Se=20 MV·A,Xt=8%p.u.,Rt=0.5%p.u.,Gt=0。
由于电磁暂态持续过程短暂,可以假设在此过程中风速不变,机组的桨距角调节装置时间常数大,还来不及动作。在短路初始时刻各机组的有功(标幺值)如表1所示。
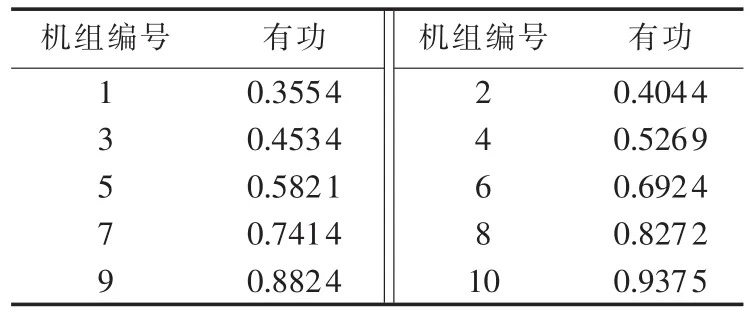
表1 短路初始时刻各机组的有功出力标幺值Tab.1 Initial fault active power of FSIG-based wind generators
根据表1中的功率信息,用K-means算法将风电场内的FSIG机组分成2个机群,得到的分群结果如表2所示。

表2 K-means算法分群结果Tab.2 Results of classification by K-means algorithm
由于采用同一种型号的风机,按照上述介绍的等值机参数聚合方法,得到等值机组的标幺值参数与单台机组的相同。为了检验等值结果,在风电场出口的联络线上施加三相对称故障以检验等值模型的正确性,故障在第3 s开始。图4为在三相短路故障情况下详细模型与等值模型故障电流对比。
由仿真结果可知,风电场多机等值模型能够在电磁暂态的时间尺度上很好地拟合详细模型,完全能满足用于测试、分析风电场并网对系统电磁暂态影响的要求。而对于传统单机等值模型,由于机组稳态运行转速相近,因此在故障初期(两周期内)单机等值模型能较好地拟合详细模型,但是各机组转速变化的差异将导致单机等值模型的误差会越来越大。
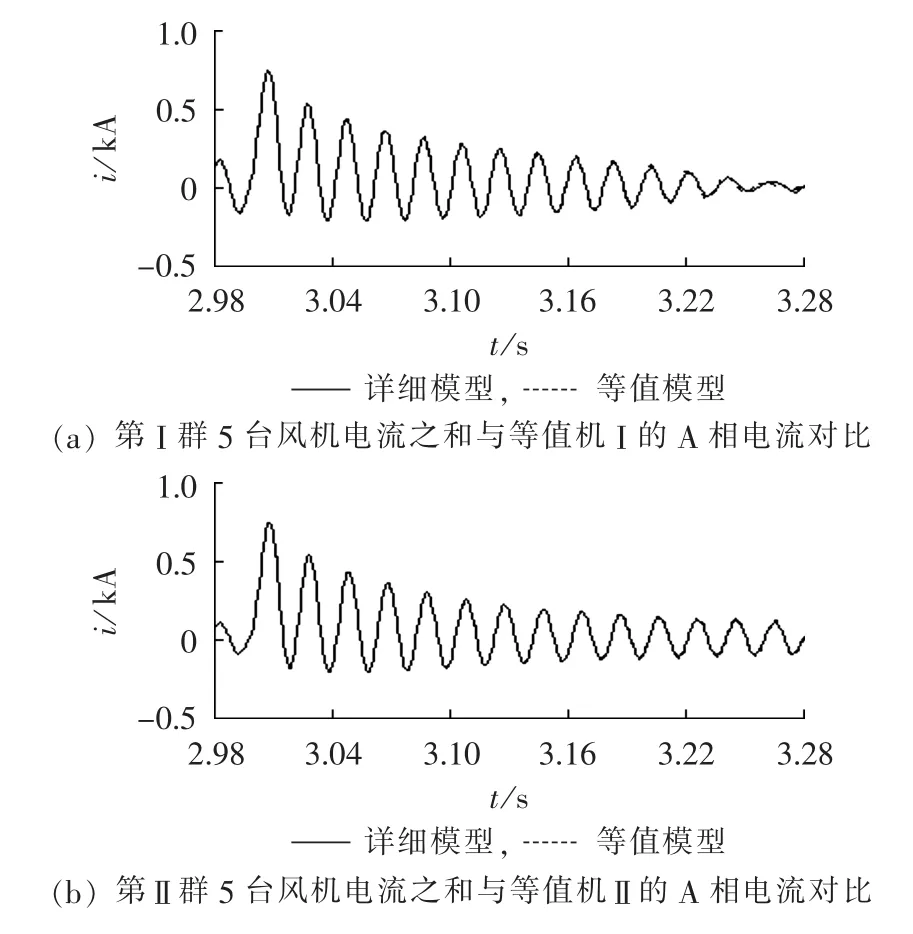

图4 风电场详细模型与其等值模型三相故障电流对比Fig.4 Comparison of three-phase short circuit current between detailed model and its equivalent model
3.2 风机型号不同
若风电场内10台FSIG风机分成2种型号,每种各5台,编号1~5机组的具体参数值同3.1节。编号6~10电机参数值为:Se=1.05 MV·A,Pe=1.0 MW,fe=50 Hz,Ue=0.69 kV,Xm=2.742 p.u.,Rs=0.0121 p.u.,Xsσ=0.1303p.u.,Rr=0.0065 p.u.,Xrσ=0.1148 p.u.,J=1.7 p.u.。
由于电磁暂态持续过程短暂,可以假设在此过程中风速不变,机组的桨距角调节装置时间常数大,还来不及动作。在短路初始时刻各机组的有功(标幺值)如表3所示。

表3 短路初始时刻各机组的有功出力标幺值Tab.3 Initial fault active power of FSIG-based wind generators
根据表3中的功率信息,用K-means算法将风电场内的FSIG机组分成2个机群,得到的分群结果如表4所示。

表4 K-means算法分群结果Tab.4 Results of classification by K-means algorithm
由于采用了2种型号的风机,按照上述介绍的基于容量加权的等值机参数聚合方法,得到2台等值机组的参数如下:等值机Ⅰ,Se=6.9 MV·A,Pe=6.5 MW,fe=50Hz,Ue=0.69 kV,Xm=3.1333 p.u.,Rs=0.011 p.u.,Xsσ=0.1442 p.u.,Rr=0.0077 p.u.,Xrσ=0.1399 p.u.,J=1.5609 p.u.;等值机Ⅱ,Se=6.35 MV·A,Pe=6 MW,fe=50 Hz,Ue=0.69 kV,Xm=3.0148 p.u.,Rs=0.0113 p.u.,Xsσ=0.1401 p.u.,Rr=0.0073 p.u.,Xrσ=0.1319 p.u.,J=1.5992 p.u.。
为了检验等值结果,在风电场出口的联络线上施加三相对称故障,检验等值模型和详细模型的拟合程度,故障在第3 s开始。图5为在三相短路故障情况下详细模型与等值模型故障电流对比。
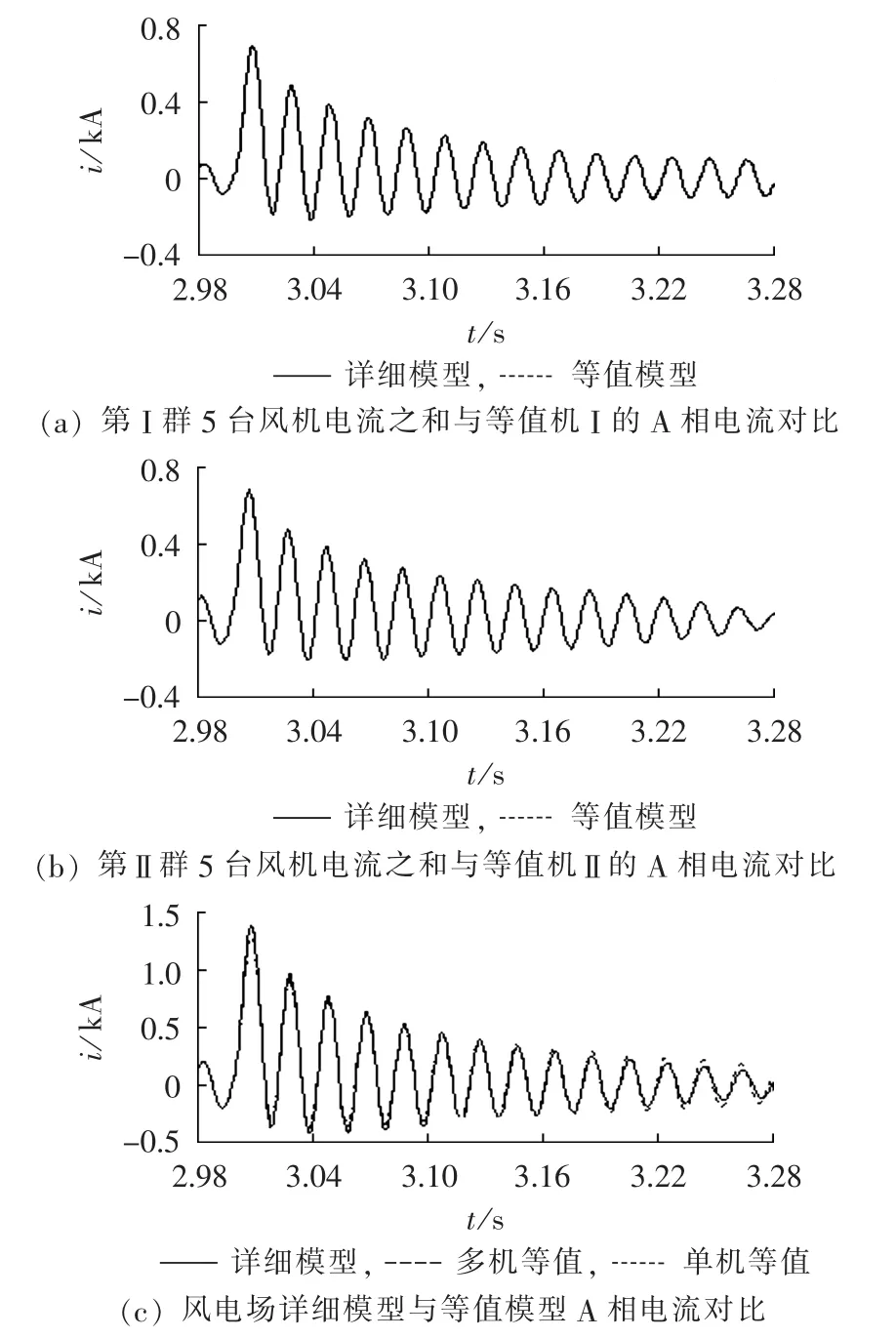
图5 风电场详细模型与其等值模型三相故障电流对比Fig.5 Comparison of three-phase short circuit current between detailed model and its equivalent model
由上述的仿真结果可知,在风电场内包含2种型号FSIG风机的情况下,经K-means算法分群后,利用基于容量加权聚合法得到的FSIG风机等值模型能够在电磁暂态的时间尺度上很好地拟合详细模型,完全能满足用于测试、分析风电场并网对系统电磁暂态特征与继电保护影响的要求。同样,对于传统单机等值模型,即使在故障初期,单机等值模型的误差也已经很大,难以满足继电保护故障分析的要求。
4 结语
本文提出了采用FSIG故障初始时刻标幺值功率信息作为划分机群的指标,采用K-means分类算法实现对风电场内风机的分群。针对同一个风电场内可能含有多种型号的FSIG风机的情况,采用基于容量加权的聚合算法计算FSIG等值机的相关参数,过程简单,适用于工程实际。在PSCAD/EMTDC软件平台上建立风电场及其等值模型,对比两者在相同故障条件下的仿真结果,克服了传统单机等值模型精度不足的问题,验证了等值方案的有效性。
